We can represent the electrical relationships in the primitive machine in an equivalent circuit as shown in Figure 1.15.
The resistance of the conductor and the motional e.m.f. together represent in circuit terms what is happening in the conductor (though in reality the e.m.f. and the resistance are distributed, not lumped as separate items). The externally applied source that drives the current is represented by the voltage V on the left (the old-fashioned battery symbol being deliberately used to differentiate the applied voltage V from the induced e.m.f. E). We note that the induced motional e.m.f. is shown as opposing the applied voltage, which applies in the ‘motoring’ condition we have been discussing. Applying KirchofFs law we obtain the voltage equation as
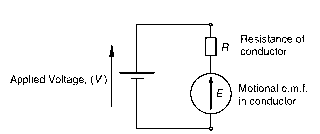
Figure 1.15 Equivalent circuit of primitive d.c. motor
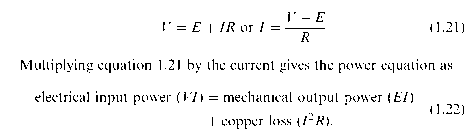
(Note that the term ‘copper loss’ used in equation 1.22 refers to the heat generated by the current in the windings: all such losses in electric motors are referred to in this way, even when the conductors are made of aluminium or bronze!)
It is worth seeing what can be learned from these equations because, as noted earlier, this simple elementary ‘motor’ encapsulates all the essential features of real motors. Lessons which emerge at this stage will be invaluable later, when we look at the way actual motors behave.
If the e.m.f. E is less than the applied voltage V, the current will be positive, and electrical power will flow from the source, resulting in motoring action. On the other hand if E is larger than V, the current will low back to the source, and the conductor will be acting as a generator. This inherent ability to switch from motoring to generating without any interference by the user is an extremely desirable property of electromagnetic energy converters. Our primitive set-up is simply a machine which is equally at home acting as motor or generator.
A further important point to note is that the mechanical power (the first term on the right hand side of equation 1.22) is simply the motional e.m.f. multiplied by the current. This result is again universally applicable, and easily remembered. We may sometimes have to be a bit careful if the e.m.f. and the current are not simple d.c. quantities, but the basic idea will always hold good.
Finally, it is obvious that in a motor we want as much as possible of the electrical input power to be converted to mechanical output power, and as little as possible to be converted to heat in the conductor. Since
the output power is EI, and the heat loss is I2R we see that ideally we want EI to be much greater than I2R, or in other words E should be much greater than IR. In the equivalent circuit (Figure 1.15) this means that the majority of the applied voltage V is accounted for by the motional e.m.f. (E), and only a little of the applied voltage is used in overcoming the resistance.
Motoring condition
Motoring implies that the conductor is moving in the same direction as the electromagnetic force (BIl), and at a speed such that the back e.m.f. (Blv) is less than the applied voltage V. In the discussion so far, we have assumed that the load is constant, so that under steady-state conditions the current is the same at all speeds, the voltage being increased with speed to take account of the motional e.m.f. This was a helpful approach to take in order to derive the steady-state power relationships, but is seldom typical of normal operation. We therefore turn to how the moving conductor will behave under conditions where the applied voltage V is constant, since this corresponds more closely with the normal operations of a real motor.
In the next section, matters are inevitably more complicated than we have seen so far because we include consideration of how the motor increases from one speed to another, as well as what happens under steady-state conditions. As in all areas of dynamics, study of the transient behaviour of our primitive linear motor brings into play additional parameters such as the mass of the conductor (equivalent to the inertia of a real rotary motor) which are absent from steady-state considerations.
Behaviour with no mechanical load
In this section we assume that the hanging weight has been removed, and that the only force on the conductor is its own electromagnetically generated one. Our primary interest will be in what determines the steady speed of the primitive motor, but we must begin by considering what happens when we first apply the voltage.
With the conductor stationary when the voltage V is applied, the current will immediately rise to a value of V/R, since there is no motional e.m.f. and the only thing which limits the current is the resistance. (Strictly we should allow for the effect of inductance in delaying the rise of current, but we choose to ignore it here in the interests of simplicity.) The resistance will be small, so the current will be large, and a high force will therefore be developed on the conductor. The conductor will therefore accelerate at a rate equal to the force on it divided by its mass.
As it picks up speed, the motional e.m.f. (equation 1.20) will grow in proportion to the speed. Since the motional e.m.f. opposes the applied voltage, the current will fall (equation 1.21), so the force and hence the acceleration will reduce, though the speed will continue to rise. The
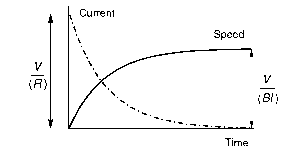
Figure 1.16 Dynamic (run-up) behaviour of primitive d.c. motor with no mechanical load speed will increase as long as there is an accelerating force, i.e. as long as there is current in the conductor. We can see from equation 1.21 that the current will finally fall to zero when the speed reaches a level at which the motional e.m.f. is equal to the applied voltage. The speed and current therefore vary as shown in Figure 1.16: both curves have the exponential shape which characterises the response of systems governed by a first-order differential equation. The fact that the steady-state current is zero is in line with our earlier observation that the mechanical load (in this case zero) determines the steady-state current.
We note that in this idealised situation (in which there is no load applied, and no friction forces), the conductor will continue to travel at a constant speed, because with no nett force acting on it there is no acceleration. Of course, no mechanical power is being produced, since we have assumed that there is no opposing force on the conductor, and there is no input power because the current is zero. This hypothetical situation nevertheless corresponds closely to the so-called ‘no-load’ condition in a motor, the only diference being that a motor will have some friction (and therefore it will draw a small current), whereas we have assumed no friction in order to simplify the discussion.
Although no power is required to keep the frictionless and unloaded conductor moving once it is up to speed, we should note that during the whole of the acceleration phase the applied voltage was constant and the input current fell progressively, so that the input power was large at first but tapered-off as the speed increased. During this run-up time energy was continually being supplied from the source: some of this energy is wasted as heat in the conductor, but much of it is stored as kinetic energy, and as we will see later, can be recovered.
An elegant self-regulating mechanism is evidently at work here. When the conductor is stationary, it has a high force acting on it, but this force tapers-of as the speed rises to its target value, which corresponds
to the back e.m.f. being equal to the applied voltage. Looking back at the expression for motional e.m.f. (equation 1.18), we can obtain an expression for the no-load speed (vo) by equating the applied voltage and the back e.m.f., which gives
![]()
Equation 1.23 shows that the steady-state no-load speed is directly proportional to the applied voltage, which indicates that speed control can be achieved by means of the applied voltage. We will see later that one of the main reasons why d.c. motors held sway in the speed-control arena for so long is that their speed could be controlled simply by controlling the applied voltage.
Rather more surprisingly, equation 1.23 reveals that the speed is inversely proportional to the magnetic flux density, which means that the weaker the field, the higher the steady-state speed. This result can cause raised eyebrows, and with good reason. Surely, it is argued, since the force is produced by the action of the field, the conductor will not go as fast if the field was weaker. This view is wrong, but understandable. The law in the argument is to equate force with speed. When the voltage is first applied, the force on the conductor certainly will be less if the field is weaker, and the initial acceleration will be lower. But in both cases the acceleration will continue until the current has fallen to zero, and this will only happen when the induced e.m.f. has risen to equal the applied voltage. With a weaker field, the speed needed to generate this e.m.f. will be higher than with a strong field: there is ‘less flux’, so what there is has to be cut at a higher speed to generate a given e.m.f. The matter is summarised in Figure 1.17, which shows how the speed will rise for a given applied voltage, for ‘full’ and ‘half fields respectively. Note that the initial acceleration (i.e. the slope of the speed-time curve) in the half-
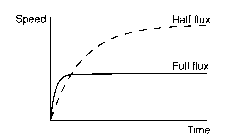
Figure 1.17 Effect of flux density on the acceleration and steady running speed of primitive d.c. motor with no mechanical load flux case is half that of the full-flux case, but the final steady speed is twice as high. In real d.c. motors, the technique of reducing the flux density in order to increase speed is known as ‘field weakening’.
Behaviour with a mechanical load
Suppose that, with the primitive linear motor up to its no-load speed we suddenly attach the string carrying the weight, so that we now have a steady force (T = mg) opposing the motion of the conductor. At this stage there is no current in the conductor and thus the only force on it will be T. The conductor will therefore begin to decelerate. But as soon as the speed falls, the back e.m.f. will become less than V, and current will begin to low into the conductor, producing an electromagnetic driving force. The more the speed drops, the bigger the current, and hence the larger the force developed by the conductor. When the force developed by the conductor becomes equal to the load (T), the deceleration will cease, and a new equilibrium condition will be reached. The speed will be lower than at no-load, and the conductor will now be producing continuous mechanical output power, i.e. acting as a motor.
Since the electromagnetic force on the conductor is directly proportional to the current, it follows that the steady-state current is directly proportional to the load which is applied, as we saw earlier. If we were to explore the transient behaviour mathematically, we would ind that the drop in speed followed the same first-order exponential response that we saw in the run-up period. Once again the self-regulating property is evident, in that when load is applied the speed drops just enough to allow sufficient current to flow to produce the force required to balance the load. We could hardly wish for anything better in terms of performance, yet the conductor does it without any external intervention on our part. Readers who are familiar with closed-loop control systems will probably recognise that the reason for this excellent performance is that the primitive motor possesses inherent negative speed feedback via the motional e.m.f. This matter is explored more fully in the Appendix.
Returning to equation 1.21, we note that the current depends directly on the difference between V and E, and inversely on the resistance. Hence for a given resistance, the larger the load (and hence the steady-state current), the greater the required difference between V and E, and hence the lower the steady running speed, as shown in Figure 1.18.
We can also see from equation 1.21 that the higher the resistance of the conductor, the more it slows down when a given load is applied. Conversely, the lower the resistance, the more the conductor is able to hold its no-load speed in the face of applied load. This is also illustrated
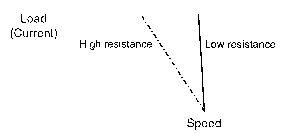
Figure 1.18 Influence of resistance on the ability of the motor to maintain speed when load is applied in Figure 1.18. We can deduce that the only way we could obtain an absolutely constant speed with this type of motor is for the resistance of the conductor to be zero, which is of course not possible. Nevertheless, real d.c. motors generally have resistances which are small, and their speed does not fall much when load is applied – a characteristic which for most applications is highly desirable.
We complete our exploration of the performance when loaded by asking how the flux density inluences behaviour. Recalling that the electromagnetic force is proportional to the flux density as well as the current, we can deduce that to develop a given force, the current required will be higher with a weak flux than with a strong one. Hence in view of the fact that there will always be an upper limit to the current which the conductor can safely carry, the maximum force which can be developed will vary in direct proportion to the flux density, with a weak flux leading to a low maximum force and vice-versa. This underlines the importance of operating with maximum flux density whenever possible.
We can also see another disadvantage of having a low flux density by noting that to achieve a given force, the drop in speed will be disproportionately high when we go to a lower flux density. We can see this by imagining that we want a particular force, and considering how we achieve it firstly with full flux, and secondly with half flux. With full flux, there will be a certain drop in speed which causes the motional e.m.f. to fall enough to admit the required current. But with half the flux, for example, twice as much current will be needed to develop the same force. Hence the motional e.m.f. must fall by twice as much as it did with full flux. However, since the flux density is now only half, the drop in speed will have to be four times as great as it was with full flux. The half-flux ‘motor’ therefore has a load characteristic with a load/speed gradient four times more droopy than the full-flux one. This is shown in Figure 1.19; the applied voltages having been adjusted so that in both
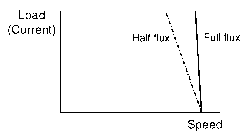
Figure 1.19 Influence of flux on the drop in steady running speed when load is applied cases the no-load speed is the same. The half-flux motor is clearly inferior in terms of its ability to hold the set speed when the load is applied.
We may be tempted to think that the higher speed which we can obtain by reducing the flux somehow makes for better performance, but we can now see that this is not so. By halving the flux, for example, the no-load speed for a given voltage is doubled, but when the load is raised until rated current is lowing in the conductor, the force developed is only half, so the mechanical power is the same. We are in effect trading speed against force, and there is no suggestion of getting something for nothing.
Relative magnitudes of V and E, and efficiency
Invariably we want machines which have high efficiency. From equation 1.20, we see that to achieve high efficiency, the copper loss (I2R) must be small compared with the mechanical power (EI), which means that the resistive volt-drop in the conductor (IR) must be small compared with either the induced e.m.f. (E) or the applied voltage (V). In other words we want most of the applied voltage to be accounted for by the ‘useful’ motional e.m.f., rather than the wasteful volt drop in the wire. Since the motional e.m.f. is proportional to speed, and the resistive volt drop depends on the conductor resistance, we see that a good energy converter requires the conductor resistance to be as low as possible, and the speed to be as high as possible.
To provide a feel for the sort of numbers likely to be encountered, we can consider a conductor with resistance of 0.5 V, carrying a current of 4 A, and moving at a speed such that the motional e.m.f. is 8 V. From equation 1.19, the supply voltage is given by
V = E + IR = 8 + (4 x 0.5) = 10 volts
Hence the electrical input power (VI) is 40 watts, the mechanical output power (EI) is 32 watts, and the copper loss (I2R) is 8 watts, giving an efficiency of 80%.
If the supply voltage was doubled (i.e. V = 20 volts), however, and the resisting force is assumed to remain the same (so that the steady-state current is still 4 A), the motional e.m.f. is given by equation 1.19 as
E = 20 – (4 x 0.5) = 18 volts
which shows that the speed will have rather more than doubled, as expected. The electrical input power is now 80 watts, the mechanical output power is 72 watts, and the copper loss is still 8 watts. The efficiency has now risen to 90%, underlining the fact that the energy conversion process gets better at higher speeds.
The ideal situation is clearly one where the term IR in equation 1.19 is negligible, so that the back e.m.f. is equal to the applied voltage. We would then have an ideal machine with an efficiency of 100%, in which the steady-state speed would be directly proportional to the applied voltage and independent of the load.
In practice the extent to which we can approach the ideal situation discussed above depends on the size of the machine. Tiny motors, such as those used in wrist-watches, are awful, in that most of the applied voltage is used up in overcoming the resistance of the conductors, and the motional e.m.f. is very small: these motors are much better at producing heat than they are at producing mechanical output power! Small machines, such as those used in hand tools, are a good deal better with the motional e.m.f. accounting for perhaps 70-80% of the applied voltage. Industrial machines are very much better: the largest ones (of many hundreds of kW) use only one or two percent of the applied voltage in overcoming resistance, and therefore have very high efficiencies.
Analysis of primitive motor – conclusions
All of the lessons learned from looking at the primitive motor will find direct parallels in almost all of the motors we look at in the rest of this topic, so it is worth reminding ourselves of the key points.
Firstly, we will make frequent reference to the formula for the force (F) on a conductor in a magnetic ield, i.e.
F = BIl (1.24)
and to the formula for the motional induced e.m.f, (E) i.e.
![]()
where B is the magnetic flux density, I is the current, l is the length of conductor and v is the velocity perpendicular to the field. These equations form the theoretical underpinning on which our understanding of motors will rest.
Secondly, we have seen that the speed at which the primitive motor runs unloaded is determined by the applied voltage, while the current that the motor draws is determined by the mechanical load. Exactly the same results will hold when we examine real d.c. motors, and very similar relationships will also emerge when we look at the induction motor.
