Specific loadings
A design compromise is inevitable in the crucial air-gap region, and designers constantly have to exercise their skills to achieve the best balance between the conflicting demands on space made by the flux (radial) and the current (axial).
As in most engineering design, guidelines emerge as to what can be achieved in relation to particular sizes and types of machines, and motor designers usually work in terms of two parameters, the specific magnetic loading, and the specific electric loading. These parameters have a direct bearing on the output of the motor, as we will now see.
The specific magnetic loading (B) is the average of the magnitude of the radial flux density over the entire cylindrical surface of the rotor. Because of the slotting, the average flux density is always less than the flux density in the teeth, but in order to calculate the magnetic loading we picture the rotor as being smooth, and calculate the average flux

Plate 1.1 Totally enclosed fan-ventilated (TEFV) cage induction motor. This particular example is rated at 200 W (0.27 h.p.) at 1450 rev/min, and is at the lower end of the power range for 3-phase versions. The case is of cast aluminium, with cooling air provided by the covered fan at the non-drive end. Note the provision for alternative mounting. (Photograph by courtesy of Brook Crompton) density by dividing the total radial flux from each ‘pole’ by the surface area under the pole.
The specific electric loading (usually denoted by the symbol (A), the A standing for Amperes) is the axial current per metre of circumference on the rotor. In a slotted rotor, the axial current is concentrated in the conductors within each slot, but to calculate A we picture the total current to be spread uniformly over the circumference (in a manner similar to that shown in Figure 1.12, but with the individual conductors under each pole being represented by a uniformly distributed ‘current sheet’). For example, if under a pole with a circumferential width of 10 cm we find that there are five slots, each carrying a current of 40 A,
![]()
Many factors influence the values which can be employed in motor design, but in essence the specific magnetic and electric loadings are limited by the properties of the materials (iron for the flux, and copper for the current), and by the cooling system employed to remove heat losses.
The specific magnetic loading does not vary greatly from one machine to another, because the saturation properties of most core steels are similar. On the other hand, quite wide variations occur in the specific electric loadings, depending on the type of cooling used.
Despite the low resistivity of the copper conductors, heat is generated by the low of current, and the current must therefore be limited to a value such that the insulation is not damaged by an excessive temperature rise. The more effective the cooling system, the higher the electric loading can be. For example, if the motor is totally enclosed and has no internal fan, the current density in the copper has to be much lower than in a similar motor which has a fan to provide a continuous flow of ventilating air. Similarly, windings which are fully impregnated with varnish can be worked much harder than those which are surrounded by air, because the solid body of encapsulating varnish provides a much better thermal path along which the heat can low to the stator body. Overall size also plays a part in determining permissible electric loading, with large motors generally having higher values than small ones.
In practice, the important point to be borne in mind is that unless an exotic cooling system is employed, most motors (induction, d.c. etc.) of a particular size have more or less the same specific loadings, regardless of type. As we will now see, this in turn means that motors of similar size have similar torque capabilities. This fact is not widely appreciated by users, but is always worth bearing in mind.
Torque and motor volume
In the light of the earlier discussion, we can obtain the total tangential force by first considering an area of the rotor surface of width w and length L. The axial current flowing in the width w is given by I = wA, and on average all of this current is exposed to radial flux density B,so the tangential force is given (from equation 1.2) by B x wA x L. The area of the surface is wL, so the force per unit area is B x A. We see that the product of the two specific loadings expresses the average tangential stress over the rotor surface.
To obtain the total tangential force we must multiply by the area of the curved surface of the rotor, and to obtain the total torque we multiply the total force by the radius of the rotor. Hence for a rotor of diameter D and length L, the total torque is given by
![]()
This equation is extremely important. The term D2L is proportional to the rotor volume, so we see that for given values of the specific magnetic and electric loadings, the torque from any motor is proportional to the rotor volume. We are at liberty to choose a long thin rotor or a short fat one, but once the rotor volume and specific loadings are specified, we have effectively determined the torque.
It is worth stressing that we have not focused on any particular type of motor, but have approached the question of torque production from a completely general viewpoint. In essence our conclusions reflect the fact that all motors are made from iron and copper, and differ only in the way these materials are disposed. We should also acknowledge that in practice it is the overall volume of the motor which is important, rather than the volume of the rotor. But again we find that, regardless of the type of motor, there is a fairly close relationship between the overall volume and the rotor volume, for motors of similar torque. We can therefore make the bold but generally accurate statement that the overall volume of a motor is determined by the torque it has to produce. There are of course exceptions to this rule, but as a general guideline for motor selection, it is extremely useful.
Having seen that torque depends on rotor volume, we must now turn our attention to the question of power output.
Specific output power – importance of speed
Before deriving an expression for power, a brief digression may be helpful for those who are more familiar with linear rather than rotary systems.
In the SI system, the unit of work or energy is the Joule (J). One joule represents the work done by a force of 1 newton moving 1 metre in its own direction. Hence the work done (W) by a force F which moves a distance d is given by
![]()
With F in newtons and d in metres, Wis clearly in newton-metres (Nm), from which we see that a newton-metre is the same as a joule.
In rotary systems, it is more convenient to work in terms of torque and angular distance, rather than force and linear distance, but these are closely linked as we can see by considering what happens when a tangential force F is applied at a radius r from the centre of rotation. The torque is simply given by
T = F x r.
Now suppose that the arm turns through an angle U, so that the circumferential distance travelled by the force is r x U. The work done by the force is then given by
![]()
We note that whereas in a linear system work is force times distance, in rotary terms work is torque times angle. The units of torque are newton-metres, and the angle is measured in radians (which is dimensionless), so the units of work done are Nm, or Joules, as expected. (The fact that torque and work (or energy) are measured in the same units does not seem self-evident to this author!)
To find the power, or the rate of working, we divide the work done by the time taken. In a linear system, and assuming that the velocity remains constant, power is therefore given by
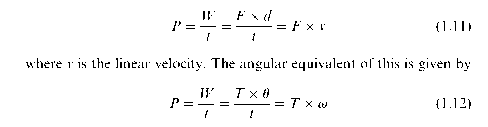
where v is the (constant) angular velocity, in radians per second.
We can now express the power output in terms of the rotor dimensions and the specific loadings, using equation 1.9 which yields
![]()
Equation 1.13 emphasises the importance of speed in determining power output. For given specific and magnetic loadings, if we want a motor of a given power we can choose between a large (and therefore expensive) low-speed motor or a small (and cheaper) high-speed one. The latter choice is preferred for most applications, even if some form of speed reduction (using belts or gears) is needed, because the smaller motor is cheaper. Familiar examples include portable electric tools, where rotor speeds of 12 000 rev/min or more allow powers of hundreds of watts to be obtained, and electric traction: wherein both cases the high motor speed is geared down for the final drive. In these examples, where volume and weight are at a premium, a direct drive would be out of the question.
The significance of speed is underlined when we rearrange equation 1.13 to obtain an expression for the specific power output (power per unit rotor volume), Q, given by
![]()
To obtain the highest possible specific output for given values of the specific magnetic and electric loadings, we must clearly operate the motor at the highest practicable speed. The one obvious disadvantage of a small high-speed motor and gearbox is that the acoustic noise (both from the motor itself and the from the power transmission) is higher than it would be from a larger direct drive motor. When noise must be minimised (for example in ceiling fans), a direct drive motor is therefore preferred, despite its larger size.
