We now turn away from considerations of what determines the overall capability of a motor to what is almost the other extreme, by examining the behaviour of a primitive linear machine which, despite its obvious simplicity, encapsulates all the key electromagnetic energy conversion processes that take place in electric motors. We will see how the process of conversion of energy from electrical to mechanical form is elegantly represented in an ‘equivalent circuit’ from which all the key aspects of motor behaviour can be predicted. This circuit will provide answers to such questions as ‘how does the motor automatically draw in more power when it is required to work’, and ‘what determines the steady
speed and current’. Central to such questions is the matter of motional e.m.f., which is explored next.
We have already seen that force (and hence torque) is produced on current-carrying conductors exposed to a magnetic field. The force is given by equation 1.2, which shows that as long as the flux density and current remain constant, the force will be constant. In particular, we see that the force does not depend on whether the conductor is stationary or moving. On the other hand, relative movement is an essential requirement in the production of mechanical output power (as distinct from torque), and we have seen that output power is given by the equation P = Tv. We will now see that the presence of relative motion between the conductors and the field always brings ‘motional e.m.f.’ into play; and we will see that this motional e.m.f. plays a key role in quantifying the energy conversion process.
Elementary motor – stationary conditions
The primitive linear machine is shown pictorially in Figure 1.13 and in diagrammatic form in Figure 1.14.
It consists of a conductor of active2 length l which can move horizontally perpendicular to a magnetic flux density B.
It is assumed that the conductor has a resistance (R), that it carries a d.c. current (I), and that it moves with a velocity (v) in a direction perpendicular to the field and the current (see Figure 1.14). Attached to the conductor is a string which passes over a pulley and supports a weight: the tension in the string acting as a mechanical ‘load’ on the rod. Friction is assumed to be zero.
We need not worry about the many difficult practicalities of making such a machine, not least how we might manage to maintain electrical connections to a moving conductor. The important point is that although
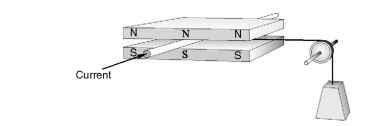
Figure 1.13 Primitive linear d.c. motor
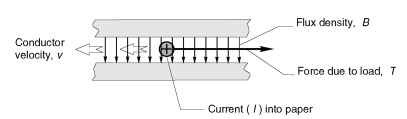
Figure 1.14 Diagrammatic sketch of primitive linear d.c. motor
this is a hypothetical set-up, it represents what happens in a real motor, and it allows us to gain a clear understanding of how real machines behave before we come to grips with much more complex structures.
We begin by considering the electrical input power with the conductor stationary (i.e. v = 0). For the purpose of this discussion we can suppose that the magnetic field (B) is provided by permanent magnets. Once the field has been established (when the magnet was first magnetised and placed in position), no further energy will be needed to sustain the field, which is just as well since it is obvious that an inert magnet is incapable of continuously supplying energy. It follows that when we obtain mechanical output from this primitive ‘motor’, none of the energy involved comes from the magnet. This is an extremely important point: the field system, whether provided from permanent magnets or ‘exciting’ windings, acts only as a catalyst in the energy conversion process, and contributes nothing to the mechanical output power.
When the conductor is held stationary the force produced on it (BIl) does no work, so there is no mechanical output power, and the only electrical input power required is that needed to drive the current through the conductor. The resistance of the conductor is R, the current through it is I, so the voltage which must be applied to the ends of the rod from an
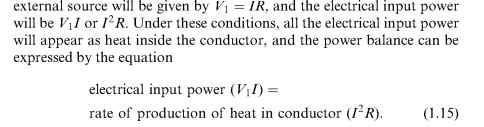
Although no work is being done because there is no movement, the stationary condition can only be sustained if there is equilibrium of forces. The tension in the string (T) must equal the gravitational force on the mass (mg), and this in turn must be balanced by the electromagnetic
force on the conductor (BIl). Hence under stationary conditions the current must be given by
![]()
This is our first indication of the link between the mechanical and electric worlds, because we see that in order to maintain the stationary condition, the current in the conductor is determined by the mass of the mechanical load. We will return to this link later.
Power relationships – conductor moving at constant speed
Now let us imagine the situation where the conductor is moving at a constant velocity (v) in the direction of the electromagnetic force that is propelling it. What current must there be in the conductor, and what voltage will have to be applied across its ends?
We start by recognising that constant velocity of the conductor means that the mass (m) is moving upwards at a constant speed, i.e. it is not accelerating. Hence from Newton’s law, there must be no resultant force acting on the mass, so the tension in the string (T) must equal the weight (mg). Similarly, the conductor is not accelerating, so its nett force must also be zero. The string is exerting a braking force (T), so the electromagnetic force (BIl ) must be equal to T. Combining these conditions yields
![]()
This is exactly the same equation that we obtained under stationary conditions, and it underlines the fact that the steady-state current is determined by the mechanical load. When we develop the equivalent circuit, we will have to get used to the idea that in the steady-state one of the electrical variables (the current) is determined by the mechanical load.
With the mass rising at a constant rate, mechanical work is being done because the potential energy of the mass is increasing. This work is coming from the moving conductor. The mechanical output power is equal to the rate of work, i.e. the force (T = BIl) times the velocity (v). The power lost as heat in the conductor is the same as it was when stationary, since it has the same resistance, and the same current. The electrical input power supplied to the conductor must continue to
furnish this heat loss, but in addition it must now supply the mechanical output power. As yet we do not know what voltage will have to be applied, so we will denote it by V2. The power-balance equation now becomes
electrical input power (V2I) = rate of production of heat in conductor
+ mechanical output power = I2R + (BIl )v (1.18)
We note that the first term on the right hand side of equation 1.18 represent the heating efect, which is the same as when the conductor was stationary, while the second term represents the additional power that must be supplied to provide the mechanical output. Since the current is the same but the input power is now greater, the new voltage V2 must be higher than V1. By subtracting equation 1.15 from equation 1.18 we obtain
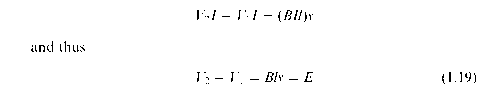
Equation 1.19 quantifies the extra voltage to be provided by the source to keep the current constant when the conductor is moving. This increase in source voltage is a reflection of the fact that whenever a conductor moves through a magnetic field, an e.m.f. (E) is induced in it.
We see from equation 1.19 that the e.m.f. is directly proportional to the flux density, to the velocity of the conductor relative to the flux, and to the active length of the conductor. The source voltage has to overcome this additional voltage in order to keep the same current flowing: if the source voltage is not increased, the current would fall as soon as the conductor begins to move because of the opposing effect of the induced e.m.f.
We have deduced that there must be an e.m.f. caused by the motion, and have derived an expression for it by using the principle of the conservation of energy, but the result we have obtained, i.e.
![]()
is often introduced as the flux-cutting’ form of Faraday’s law, which states that when a conductor moves through a magnetic field an e.m.f.
given by equation 1.20 is induced in it. Because motion is an essential part of this mechanism, the e.m.f. induced is referred to as a ‘motional e.m.f.’. The ‘flux-cutting’ terminology arises from attributing the origin of the e.m.f. to the cutting or slicing of the lines of flux by the passage of the conductor. This is a useful mental picture, though it must not be pushed too far: the flux lines are after all merely inventions which we find helpful in coming to grips with magnetic matters.
Before turning to the equivalent circuit of the primitive motor, two general points are worth noting. Firstly, whenever energy is being converted from electrical to mechanical form, as here, the induced e.m.f. always acts in opposition to the applied (source) voltage. This is reflected in the use of the term ‘back e.m.f.’ to describe motional e.m.f. in motors. Secondly, although we have discussed a particular situation in which the conductor carries current, it is certainly not necessary for any current to be flowing in order to produce an e.m.f.: all that is needed is relative motion between the conductor and the magnetic field.
