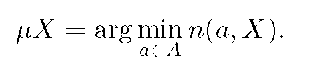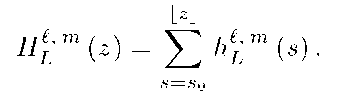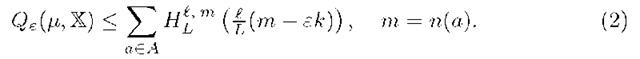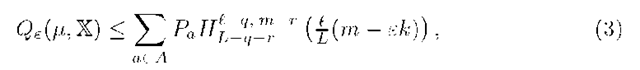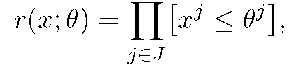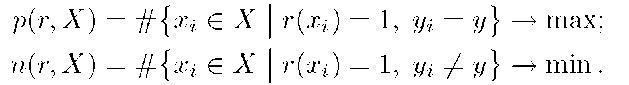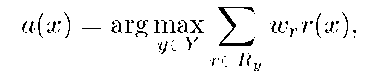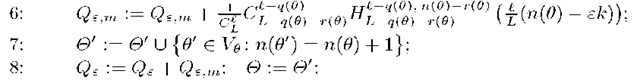Abstract
We propose a combinatorial technique for obtaining tight data dependent generalization bounds based on a splitting and connectivity graph (SC-graph) of the set of classifiers. We apply this approach to a parametric set of conjunctive rules and propose an algorithm for effective SC-bound computation. Experiments on 6 data sets from the UCI ML Repository show that SC-bound helps to learn more reliable rule-based classifiers as compositions of less overfitted rules.
Keywords: computational learning theory, generalization bounds, per-mutational probability, splitting-connectivity bounds, rule induction.
Introduction
Obtaining exact generalization bounds remains an open problem in Computational Learning Theory [1]. Experiments [8,9] have shown that two fine effects should be taken into account simultaneously to obtain exact bounds: the splitting of the set into error levels and the similarity of classifiers. Many practically used sets contain a lot of similar classifiers that differ on one object, they are called connected. In this work we develop a combinatorial approach that deals with splitting and connectivity together and gives tight or even exact bounds on probability of overfitting. We apply a new SC (splitting and connectivity) combinatorial bound to the set of conjunctive rules and propose the overfitting reduction method compatible with most usual rule induction engines.
Definitions and Notation
Let
be a set of objects and A be a set of classifiers. A binary loss function
exists such that
if a classifier a produces an error on an object x. A binary vector
of size L is called an error vector of the classifier a. Assume that all classifiers from A have pairwise different error vectors.
The number of errors of a classifier a on a sample
is defined as
. For shorter notation denote
The error rate is defined as
The learning algorithm is a mapping
that takes a training sample
and gives a classifier
Transductive (permutational) probability. Denote
the set of all
samples
of size I. Assume that all partitions of the general set X into an observed training sample X of size I and a hidden test sample
of size
can occur with equal probability The classifier
is said
to be overfitted if the discrepancy
is greater than a given nonnegative threshold e. Define the probability of overfitting as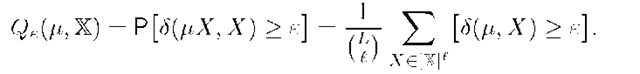 
where brackets transform a logical value into numerical one: [true] = 1, [false]=0. The inversion of a bound
is an inequality
which holds with probability at least
, where
is the inverse for
Empirical risk minimization (ERM) is a classical and perhaps most natural example of the learning algorithm:
Hypergeometric distribution. For a classifier a such that
the probability to make s errors on a sample X is given by a hypergeometric function:
, where
, argument s runs from
parameter m takes values 0,…,L.
It is assumed that
for all other integers m, s. Define the cumulative distribution function (left tail) of the hypergeometric distribution
Consider a set
containing one fixed classifier, so that
for any X. Then the probability of overfitting
transforms into the probability of large deviation between error rates in two samples X, X.
Theorem 1 (FC-bound). For a fixed classifier a such that
, for any set X and any
the probability of overfitting is given by the left tail of hypergeometric distribution:
The exact FC-bound plays a role of the Law of Large Numbers in permutational probabilistic framework because it predicts the error rate on the hidden sample from the observed one, whereas the "probability of error" is undefined here. The hypergeometric distribution is fundamental for all further bounds.
Theorem 2 (VC-bound). For any set X, any learning algorithm
and any 
the probability of over fitting is bounded by the sum of FC-bounds over A:
Further weakening this bound gives a well known form of the VC-bound:
for a case
VC-bound is highly overestimated because all classifiers make approximately equal contributions to the VC-bound. However, the set of classifiers is usually split into error rates in quite nonuniform manner. Most classifiers are unsuitable, have vanishing probability to be obtained as a result of learning and make a negligible contribution to the probability of overfitting. On the other hand, similar classifiers share their contribution, thus each of them contributes poorly again. VC theory totally ignores both advantageous effects.
Splitting and Connectivity Bounds
Define the order relation on classifiers
as a natural order on their error vectors:
for all i = 1,…,L. Introduce Hamming distance between error vectors:
Classifiers a and b are called connected if
Define the precedence relation on classifiers
The set of classifiers A can be represented by a multipartite directed graph that we call the splitting and connectivity graph (SC-graph) in which vertices are classifiers, and edges (a, b) are pairs of classifiers such that
Partite
subsets
are called error layers, m = 0,…,L. Each edge of the SC-graph (a, b) can be uniquely labeled by an object
such that
Upper connectivity
of a classifier a is the number of edges leaving the vertex a.
Inferiority
of a classifier a is the number of different objects assigned to edges below the vertex a in the SC-graph. If a correct classifier
exists such that
then inferiority is equal to the number of errors,
. In general case
Theorem 3 (SC-bound). If ^ is ERM then for any
the probability of overfitting is bounded by the weighted sum of FC-bounds over the set A:
where q = q(a) is upper connectivity, r = r(a) is inferiority, m = n(a) is the number of errors of classifier
is an upper bound on the probability to learn the classifier a,
where q = q(a) is upper connectivity, r = r(a) is inferiority, m = n(a) is the number of errors of classifier
is an upper bound on the probability to learn the classifier a,
The weight Pa decreases exponentially as connectivity q(a) and inferiority r(a) increase. This fact has two important consequences.
First, connected sets of classifiers are less subjected to overfitting. Not only the fact of connectedness but better the number of connections is important.
Second, only lower layers contribute significantly to the probability of overfit-ting. This fact encourages effective procedures for SC-bound computation.
SC-bound (3) is much more tight than the VC-bound (2). It transforms to the VC-bound by substituting q = r = 0, i. e. by disregarding the SC-graph.
SC-Bound for Threshold Conjunctive Rules
Consider a classification problem with labels
assigned to each object
respectively. Consider a parametric set R of conjunctive rules
where
is a vector of numerical features of object
is a subset of features,
is a threshold parameter for j-th feature. An object x is said to be covered by the rule
A rule induction system learns a rule set
for each class
from a training set X. Two criteria are optimized simultaneously to select useful rules — the number of positive and negative examples covered by r, respectively:
In practice the two-criteria optimization task is reduced to one-criterion task by means of heuristic function H(p, n). Examples of H are Fisher’s exact test [5], entropy, Gini index, x2- and w2-tests, and many others [4].
Rule based classifier. After learning the rule sets Ry for all y G Y the classifier can be buildup as a composition of rules, e.g. as a weighted voting:
where weights
are learned from the training set X. So, there are three things to learn: (1) thresholds
for each subset J; (2) feature subset J for each rule r; (3) weight wr for each rule r. Respectively, there are three reasons for overfitting. In this work we use SC-bound to estimate overfitting resulting from thresholds learning and build a criterion for feature subset selection, with motivation that a good classifier can be hardly build up from overfitted rules.
The idea of heuristic modification is to obtain the SC-bound on p and n for a fixed J; then to get inverted estimates that hold with probability at least 1 — r/:
and to use them instead of p, n in a heuristic
The modified heuristic H’ gives a more accurate features selection criterion that takes into account the overfitting resulting from thresholds learning.
Specialization of SC-bound for conjunctive rules. Define the binary loss function as
for any rule r of class y. For the sake of simplicity suppose that all values
are pairwise different for each feature j, features take integers 1,…,L and the thresholds take integers 0,…,L.
For any pair of vectors
define an order relation
Define
A boundary point of the subset
is a vector
Note that
for any
A boundary object of the subset
is any object
A boundary subset is a subset
such that all objects
are its boundary objects. Each boundary subset is unambiguously defined by its boundary point. Empty set is a boundary subset with boundary point
The following theorem states that the sum over all rules in SC-bound (3) can be calculated by running over all boundary subsets.
Theorem 4. The set of rules
where S runs over all boundary subsets coincide with the set of all rules
having pairwise different error vectors.
Then our idea is to iterate all rules (really, boundary subsets) from bottom to upper levels of SC-graph and use early stopping to bypass rules from higher levels that make no significant contribution to the SC-bound. To do this effectively we first consider an algorithm for the neighbor search of boundary subsets.
Searching the set of neighbor rules. Consider a rule
defined by a threshold vector
Its neighborhood
is defined as a set of all rules
that differ from
on single object. Algorithm 4.1 iterates all neighbor rules 
such that
is a boundary point of a boundary subset.
At first stage (steps 1-5) neighbor rules
are produced from 0 by de creasing thresholds
For each boundary object thresholds 0 decrease until another object becomes boundary.
At second stage (steps 6-11) neighbor rules
are produced from 0 by increasing thresholds
This is a more involved case that requires a recursive procedure. The preliminary work at steps 6, 7 helps to reduce further search by determining the maximal boundary 0 that neighbor rules may fall in.
Each object
can have one of three states: x.checked
, what enables to avoid the repeated processing of objects at second stage.
Initially all objects are not checked. Then for each object
covered by the rule
but not covered by the rule
the recursive procedure Check(x) is invoked. If the rule
covers only one object x in addition to objects covered by
then x is good. Otherwise the rule
covers two objects
not covered by the rule
in such case x is bad and the procedure
Check(X) is invoked recursively with the object x. Each good object x induces the neighbor rule
which is added to the set
Algorithm 4.1 guarantee that all neighbor rules will be found. Besides it calculates all characteristics of the rule needed to calculate SC-bound:
Algorithm 4.1. Seek the neighborhood
of the rule
Require: features subset J, thresholds
class label
, general set X.
Ensure:
1:
2: for all
such that
and
for some
do
3: for all
such that
do
4:
5: AddNeighbor
6: for all
do
7:
8: for all
do
9: for all x such that
do
10: if
and x.checked = false then
11: CheckO
12: Procedure Check(x) 13: for all
such that
do
14: for all
such that
do
15: if
then
16: x.checked := bad;
17: if
checked = false then Check
18: exit;
19: x.checked := good; 20:
21: AddNeighbor
22: Procedure AddNeighbor
23: add the rule 6′ into the set of neighbors
24: if
then
25:
26: else 27:
and n(0). To avoid the exhaustive search of all objects at steps 4, 7, 9, 14 the sorting index is to be built in advance for each coordinate
Level-wise bottom-up calculation of SC-bound. Algorithm 4.2 starts from a lowest layer of classifiers. At each step it process a layer O consisting of all rules 0 that makes m = n(0) errors on general set. For each rule 0 Algorithm 4.2 calculates its contribution to the SC-bound, builds its neighborhood, and forms the (m + 1)-th layer O’ joining upper parts of all neighborhoods. The steps are repeated until layer contribution becomes sufficiently small. Note that early stopping gives a lower estimate for (3), witch is upper bound on probability of overfitting.
Experiment. We used following state-of-the art algorithms as baseline rule learners: C4.5 [7], C5.0 [6], RIPPER [2], and SLIPPER [3]. Our rule learning engine was based on breadth-first search as feature selection strategy and Fisher’s exact test (FET) as heuristic H. To build compositions of rules three algorithms has been implemented. Logistic Regression (LR) is a linear classifier that aggregates rules learned independently. Weighted Voting (WV) is a boosting-like ensemble of rules similar to SLIPPER which learns each subsequent rule from reweighted training set. Decision List (DL) is a greedy algorithm which learns each subsequent rule from training objects not covered by all previous rules.
Algorithm 4.2. SC-bound calculation for the set of conjunction rules.
Require: features subset J, class label
, set of objects X.
Ensure:
on probability of overfitting (3).
9: until the contribution of the m-th layer
becomes small.
We implemented two modifications of heuristic H’(p, n). The SC modification uses SC-bound on the probability of overfitting Qe as described above. The MC modification uses the Monte-Carlo estimation of Qe via 100 random partitions 
For both modifications we set I = k.
Table 1. Experimental results on 6 real data sets from UCI Machine Learning Repository. For each pair (task, algorithm) an average testing error obtained from 10-fold cross validation is given, in percents. For each task three best results are bold-emphasized. Algorithms 1-7 are baseline rule learners. Our algorithms: WV — Weighted Voting, DL — Decision List, SC — using heuristic modified by SC-bound, MC — using heuristic modified by Monte-Carlo estimation of the probability of overfitting.
|
algorithms |
tasks |
||||||
|
australian |
echo-card |
heart dis. |
hepatitis |
labor |
liver |
||
|
1 |
RIPPER-opt |
15.5 |
2.9 |
19.7 |
20.7 |
18.0 |
32.7 |
|
2 |
RIPPER+opt |
15.2 |
5.5 |
20.1 |
23.2 |
18.0 |
31.3 |
|
3 |
C4.5 (Tree) |
14.2 |
5.5 |
20.8 |
18.8 |
14.7 |
37.7 |
|
4 |
C4.5 (Rules) |
15.5 |
6.8 |
20.0 |
18.8 |
14.7 |
37.5 |
|
5 |
C5.0 |
14.0 |
4.3 |
21.8 |
20.1 |
18.4 |
31.9 |
|
6 |
SLIPPER |
15.7 |
4.3 |
19.4 |
17.4 |
12.3 |
32.2 |
|
7 |
LR |
14.8 |
4.3 |
19.9 |
18.8 |
14.2 |
32.0 |
|
8 |
WV |
14.9 |
4.3 |
20.1 |
19.0 |
14.0 |
32.3 |
|
9 |
DL |
15.1 |
4.5 |
20.5 |
19.5 |
14.7 |
35.8 |
|
10 |
WV+MC |
13.9 |
3.0 |
19.5 |
18.3 |
13.2 |
30.7 |
|
11 |
DL+MC |
14.5 |
3.5 |
19.8 |
18.7 |
13.8 |
32.8 |
|
12 |
wv+sc |
14.1 |
3.2 |
19.3 |
18.1 |
13.4 |
30.2 |
|
13 |
DL+SC |
14.4 |
3.6 |
19.5 |
18.6 |
13.6 |
32.3 |
Results are presented in Table 1. Initial unmodified versions of our algorithms WV and DL with FET heuristic have a performance comparable to the baseline. WV outperforms DL, what corresponds to the results of other authors. Both SC and MC modifications of the FET heuristic reduce overfitting of rules and of classifier as a whole. Both modified classifiers outperform their respective initial versions for all 6 tasks. It must be emphasized that the only modification is the rule evaluation heuristic, all other things being equal. Thus, all difference in performance is due to generalization bound used in modified FET heuristic. The difference between SC and MC results is not significant, but MC estimation is much more time consuming. A moderate looseness of the SC-bound really takes place but does not reduce its practical usefulness as a rule selection criterion.
Conclusion
This work gives a new SC (splitting and connectivity) combinatorial bound on probability of overfitting. It takes into account a fine internal structure of the set of classifiers formalized in terms of the SC-graph. For a set of threshold conjunctive rules a level-wise bottom-up algorithm with early stopping is proposed for effective SC-bound computation. The inverted SC-bound is used to modify standard rule evaluation heuristic. This modification can be build in most known rule learners. It enables to take into account an amount of overfitting resulting from thresholds learning, and then to select features subset for each rule more accurately. Experiments on six real data sets show that the proposed modification reduces overfitting significantly.
