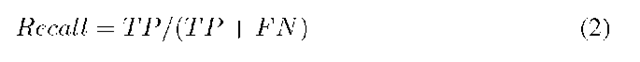N DoT: Nearest Neighbor Distance Based Outlier Detection Technique (Pattern Recognition and Machine Learning)

Abstract

In this paper, we propose a nearest neighbor based outlier detection algorithm, NDoT. We introduce a parameter termed as Nearest Neighbor Factor (NNF) to measure the degree of outlierness of a point with respect to its neighborhood. Unlike the previous outlier detection methods NDoT works by a voting mechanism. Voting mechanism binarizes the decision compared to the top-N style of algorithms. We evaluate our method experimentally and compare results of NDoT with a classical outlier detection method LOF and a recently proposed method LDOF. Experimental results demonstrate that NDoT outperforms LDOF and is comparable with LOF.

Introduction

Finding outliers in a collection of patterns is a very well known problem in the data mining field. An outlier is a pattern which is dissimilar with respect to the rest of the patterns in the dataset. Depending upon the application domain, outliers are of particular interest. In some cases presence of outliers adversely affect the conclusions drawn out of the analysis and hence need to be eliminated beforehand. In other cases outliers are the centre of interest as in the case of intrusion detection system, credit card fraud detection. There are varied reasons for outlier generation in the first place. For example outliers may be generated due to measurement impairments, rare normal events exhibiting entirely different characteristics, deliberate actions etc. Detecting outliers may lead to the discovery of truly unexpected behaviour and help avoid wrong conclusions etc. Thus irrespective of the underlying causes for outlier generation and insight inferred, these points need to be identified from a collection of patterns. There are number of methods proposed in the literature for detecting outliers [1] and are mainly of three types as distance based, density based and nearest neighbor based.

Distance based: These techniques count the number of patterns falling within a selected threshold distance R from a point x in the dataset. If the count is more than a preset number of patterns then x is considered as normal and otherwise outlier. Knorr. et. al. [2] define outlier as "an object o in a dataset D is a DB(p, T)-outlier if at least fraction p of the objects in D lies greater than distance T from o". DOLPHIN [3] is a recent work based on this definition of outlier given by Knorr.

Density based: These techniques measure density of a point x within a small region by counting number of points within a neighborhood region. Breunig et al. [4] introduced a concept of local outliers which are detected based on the local density of points. Local density of a point x depends on its k nearest neighbors points. A score known as Local Outlier Factor is assigned to every point based on this local density. All data points are sorted in decreasing order of LOF value. Points with high scores are detected as outliers. Tang et al. [5] proposed an improved version of LOF known as Connectivity Outlier Factor for sparse dataset. LOF is shown to be not effective in detecting outliers if the dataset is sparse [5,6].

Nearest neighbor based: These outlier detection techniques compare the distance of the point x with its k nearest neighbors. If x has a short distance to its k neighbors it is considered as normal otherwise it is considered as outlier. The distance measure used is largely domain and attribute dependent. Ramaswamy et al. [7] measure the distances of all the points to their kth nearest neighbors and sort the points according to the distance values. Top N number of points are declared as outliers.

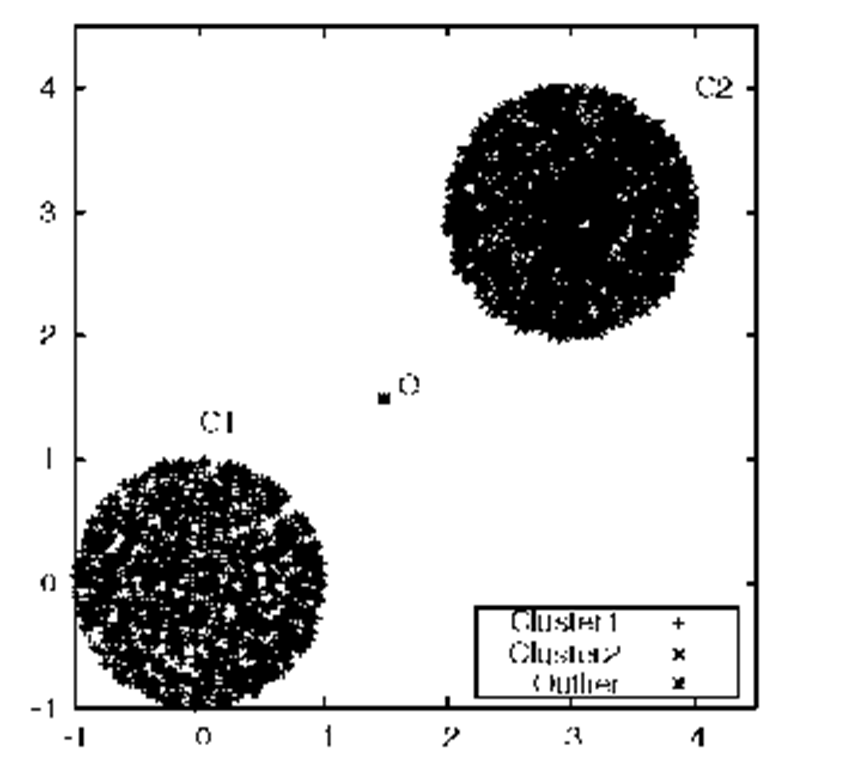
Zhang et al. [6] showed that LOF can generate high scores for cluster points if value of k is more than the cluster size and subsequently misses genuine outlier points. To overcome this problem, they proposed a distance based outlier factor called LDOF. LDOF is the ratio of k nearest neighbors average distance to k nearest neighbors inner distance. Inner distance is the average pair-wise distance of the k nearest neighbor set of a point x. A point x is declared as genuine outlier if the ratio is more than 1 else it is considered as normal. However, if an outlier point (say, O) is located between two dense clusters (Fig. 1) it fails to detect O as outlier. The LDOF of O is less than 1 as k nearest neighbors of O contain points from both the clusters. This observation can also be found in sparse data.

Fig. 1. Uniform Dataset

In this paper, we propose an outlier detection algorithm, NDoT (jVearest Neighbor .Distance Based outlier Detection Technique). We introduce a parameter termed as Nearest Neighbor Factor (NNF) to measure the degree of out-lierness of a point. Nearest Neighbor Factor (NNF) of a point with respect to one of its neighbors is the ratio of distance between the point and the neighbor, and average knn distance of the neighbor. NDoT measures NNF of a point with respect to all its neighbors individually. If NNF of the point w.r.t majority of its neighbors is more than a pre-defined threshold, then the point is declared as a potential outlier. We perform experiments on both synthetic and real world datasets to evaluate our outlier detection method.

The rest of the paper is organized as follows. Section 2 describes proposed method. Experimental results and conclusion are discussed in section 3 and section 3.2, respectively.

Fig. 2. The k nearest neighbor of x with k = 4

Proposed Outlier Detection Technique : N DoT

In this section, we develop a formal definition for Nearest Neighbor Factor (NNF) and describe the proposed outlier detection algorithm, NDoT.

Definition 1 (k Nearest Neighbor (knn) Set). Let D be a dataset and x be a point in D. For a natural number k and a distance function d, a set is called knn of x if the following two conditions hold.

1.is not unique inotherwise.

2., whereis the set of all q point(s).

Definition 2 (Average knn distance). Let NNk be the knn of a point.

Average knn distance of x is the average of distances between x and

Average knn distance

Average knn distance of a point x is the average of distances between x and its knn. If Average knn distance of x is less compared to other point y, it indicates that x’s neighborhood region is more densed compared to the region where y resides.

Definition 3 (Nearest Neighbor Factor (NNF)). Let x be a point in D and be the knn of x. The NNF of x with respect tois the ratio ofand Average knn distance of q.

The NNF of x with respect to one of its nearest neighbors is the ratio of distance between x and the neighbor, and Average knn distance of that neighbor. The proposed method NDoT calculates NNF of each point with respect to all of its knn and uses a voting mechanism to decide whether a point is outlier or not.

Algorithm 1 describes steps involved in NDoT. Given a dataset D, it calculates knn and Average knn distance for all points in D. In the next step, it computes Nearest Neighbor Factor for all points in the dataset using the previously calculated knn and Average knn distance. NDoT decides whether x is an outlier or not based on a voting mechanism. Votes are counted based on the generated NNF values with respect to all of its k nearest neighbors.

Algorithm 1. NDoT(D, k)

If is more than a threshold S (in experiments S =1.5 is considered), x is considered as outlier with respect to q. Subsequently, a vote is counted for x being an outlier point. If the number of votes are at least 2/3 of the number of nearest neighbors then x is declared as an outlier, otherwise x is a normal point.

Complexity Time and space requirements of NDoT are as follows.

1. Finding knn set and Average knn distance of all points takes time of, where n is the size of the dataset. The space requirement of the step is O(n).

2. Deciding a point x to be outlier or not takes timeFor whole dataset the step takes time of, as k is a small constant.

Thus the overall time and space requirements are, respectively.

Experimental Evaluations

In this section, we describe experimental results on different datasets. We used two synthetic and two real world datsets in our experiments. We also compared our results with classical LOF algorithm and also with one of its recent enhancement LDOF. Results demonstrate that NDoT outperforms both LOF and LDOF on synthetic datasets. We measure the Recall given by Equation 2 as an evaluation metric. Recall measures how many genuine outliers are there among the outliers detected by the algorithm. Both LDOF and LOF are of top N style algorithms. For a chosen value of N, LDOF and LOF consider N highest scored points as outliers. However, NDoT makes a binary decision about a point as either an outlier or normal. In order to compare our algorithm with LDOF and LOF we used different values of N.

where TP is number of true positive cases and FN is the number of false negative cases. It is to be noted that top N style algorithms select highest scored N points as outliers. Therefore, remaining N-TP are false positive (FP ) cases. As FP can be inferred based on the values of N and TP we do not explicitly report them for LDOF and LOF.

Synthetic Datasets

There are two synthetic datasets designed to evaluate the detection ability (Recall) of algorithms. These two experiments are briefed subsequently.

Uniform dataset. Uniform distribution dataset is a two dimensional synthetic dataset of size 3139. .It has two circular shaped clusters filled with highly densed points. There is a single outlier (say O) placed exactly in the middle of the two densed clusters as shown in the Figure 1. We ran our algorithm along with LOF and LDOF on this dataset and measured the Recall for all the three algorithms. Obtained results for different values of k are tabulated in Table 1. This table shows that, NDoT and LOF could detect the single outlier consistently while LDOF failed to detect it.

Fig. 3. Circular dataset

In case of LDOF the point O has knn set from both the clusters, thus the average inner distance is much higher than the average knn distance. This results in a LDOF value less than 1. However, NNF value of O is more than 1.5 with respect to all its neighbors q e C\ or C2. Because, q’s average knn distance is much smaller than the distance between O and q.

Table 1 shows the Recall for all the three algorithms and also the false positives for NDoT (while the number of false positives for LDOF and LOF are implicit). It can be noted that, for any dataset of this nature NDoT outperforms the other two algorithms in terms of number of false positive cases detected.

Circular dataset. This dataset has two hollow circular shaped clusters with 1000 points in each of the clusters. Four outliers are placed as shown in Figure 3. There are two outliers exactly at the centers of two circles and other two are outside.

The results on this dataset for the three algorithms are shown in the Table 2. Again we notice both NDoT and LOF consistently detect all the four outliers for all the k values while LDOF fails to detect them. Similar reasons raised for the previous experiments can be attributed to the poor performance of LDOF.

Table 1. Recall comparison for uniform dataset

k Value	NDoT		LDOF			LOF
	Recall	FP	Top 25	Top 50	Top 100	Top 25	Top 50	Top 100
5	100.00%	47	00.00%	00.00%	00.00%	100.00%	100.00%	100.00%
9	100.00%	21	00.00%	00.00%	00.00%	100.00%	100.00%	100.00%
21	100.00%	2	00.00%	00.00%	00.00%	100.00%	100.00%	100.00%
29	100.00%	0	00.00%	00.00%	00.00%	100.00%	100.00%	100.00%
35	100.00%	0	00.00%	00.00%	00.00%	100.00%	100.00%	100.00%
51	100.00%	0	00.00%	00.00%	00.00%	100.00%	100.00%	100.00%
65	100.00%	0	00.00%	00.00%	00.00%	100.00%	100.00%	100.00%

Table 2. Recall comparison for circular dataset with 4 outliers

k Value	NDoT		LDOF			LOF
	Recall	FP	Top 25	Top 50	Top 100	Top 25	Top 50	Top 100
5	100.00%	0	50.00%	100.00%	100.00%	100.00%	100.00%	100.00%
9	100.00%	0	25.00%	75.00%	100.00%	100.00%	100.00%	100.00%
15	100.00%	10	25.00%	75.00%	100.00%	100.00%	100.00%	100.00%
21	100.00%	10	25.00%	50.00%	100.00%	100.00%	100.00%	100.00%
29	100.00%	10	25.00%	50.00%	100.00%	100.00%	100.00%	100.00%

Real World Datasets

In this section, we describe experiments on two realworld datasets taken from UCI machine learning repository. Experimental results are elaborated subsequently.

Shuttle dataset. This dataset has 9 real valued attributes with 58000 instances distributed across 7 classes. In our experiments, we picked the test dataset and used class label 2 which has only 13 instances as outliers and remaining all instances as normal. In this experiment, we performed three-fold cross validation by injecting 5 out of 13 instances as outliers into randomly selected 1000 instances of the normal dataset. Results obtained by the three algorithms are shown in Table 3. It can be observed that NDoT’s performance is consistently better than LDOF and is comparable to LOF.

Table 3. Recall Comparison for Shuttle Dataset

k Value	NDoT	LDOF			LOF
		Top 25	Top 50	Top 100	Top 25	Top 50	Top 100
5	80.00%	20.00%	20.00%	26.66%	26.66%	53.33%	66.66%
9	93.33%	26.66%	33.33%	33.33%	06.66%	26.66%	93.33%
15	100.00%	20.00%	33.33%	53.33%	00.00%	26.66%	100.00%
21	100.00%	20.00%	33.33%	66.66%	00.00%	26.66%	80.00%
35	100.00%	40.00%	73.33%	73.33%	00.00%	20.00%	53.33%

Forest covertype dataset. This dataset is developed at the university of Colarado to help natural resource managers predict inventory information. This dataset has 54 attributes having a total of 581012 instances distributed across 7 cover types (classes). In our experiential, we selected the class label 6 (Douglas-fir) with 17367 instances and randomly picked 5 instances from the class 4 (Cottonwood/Willow) as outliers. Results obtained are shown in Table 4. We can notice that, NDoT outperforms both LDOF and LOF on this dataset.

Table 4. Recall Comparison for CoverType Dataset

k Value	NDoT	LDOF			LOF
		Top 25	Top 50	Top 100	Top 25	Top 50	Top 100
35	60.00%	40.00%	40.00%	40.00%	00.00%	10.00%	10.00%
51	80.00%	40.00%	40.00%	40.00%	00.00%	10.00%	10.00%

Conclusion

NDoT is a nearest neighbor based outlier detection algorithm, which works on a voting mechanism by measuring Nearest Neighbor Factor (NNF). The NNF of a point w.r. t one of its neighbor measures the degree of outlierness of the point. Experimental results demonstrated effectiveness of the NDoT on both synthetic and real world datasets.