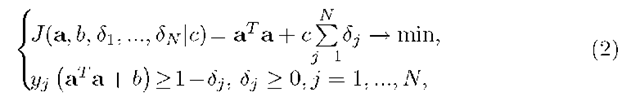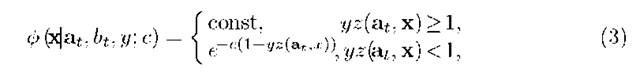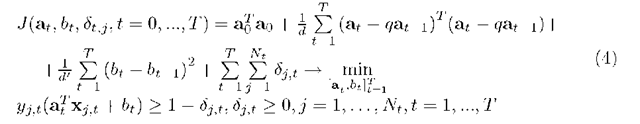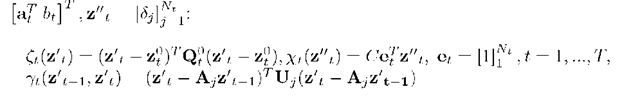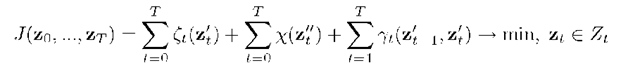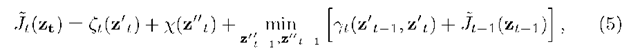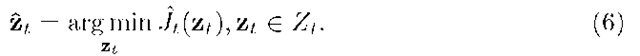Abstract
The classical learning problem of the pattern recognition in a finite-dimensional linear space of real-valued features is studied under the conditions of a non-stationary universe. The training criterion of non-stationary pattern recognition is formulated as a generalization of the classical Support Vector Machine. The respective numerical algorithm has the computation complexity proportional to the length of the training time series.
The majority of modern methods for pattern recognition works under the assumption that properties of the environment and consequently required decision rule doesn’t change in a process of data collection as well as during the exam. However, recently there have appeared many applications, in which samples of training set are entering the system over a long period of time, when the properties of the analyzed phenomenon may undergo considerable changes. The example of such problem is task of filtering irrelevant or publicity hyperlinks as a result of retrieval request. The behavior of internet advertising distributors constantly turns and it causes changes of publicity hyperlinks features that should result in the adequate correction of search mechanism. Often in this kind of tasks both the nature of changes in the environment and the fact of changes itself are hidden from direct observation and this makes learning even more difficult. In literature this problem is called concept drift [1].
At present there are three approaches to the construction of algorithms taking into account non-stationary character of decision rule: algorithms based on selecting instances, algorithms based on weighted instances and algorithms based on classifier selection and mergers. The goal of algorithms using selection of instances is the choice of prototypes which are relevant for decision rule at the present moment. As a rule, it is realized with the help of running window technology when decision rule at the present moment is made only on the basis of the instances obtained from previous time points. The examples of such algorithms can be FLORA family of algorithms [1] and TMF [2].
Algorithms based on weighting of instances [3] obtained from different time points use the ability of some learning algorithms such as Support Vector Machines (SVMs) method to assign weights to different instances. As a rule, weights are assigned to the instances according to their "age" (e.g. period of time from their obtaining).
By ensemble-based approach [5] for pattern recognition in non-stationary environment, required decision rule is made as voting or weighted voting of classifiers obtained for different conditions. For example, in the paper [4] it is proposed to cluster training samples and to construct its own classifier for each cluster.
In general, we can mark that all existing algorithms are more or less heuristic and a certain set of heuristics is determined by a specificity of the current task. In this paper we propose stochastic concept of the non-stationary environment based on Bayesian approach to the pattern recognition problem. The main instantaneous property of the non-stationary environment is understood as time-dependent separating hyperplane that in the best way describes the differences between feature vectors of samples of two classes. The proposed concept brings about the learning algorithm that is a generalization of the classical SVM for the case when the parameters of the separating hyperplane change with time.
Bayesian Definition of the Pattern Recognition Problem in Non-stationary Environment
Let every instance of the environment
is presented by a point in the linear feature space
, and its hidden membership in one of two classes is determined by an index value of the class
The paper [6] proposed a stochastic model of the universe. The main model assumption is a priori parametric distribution of the instances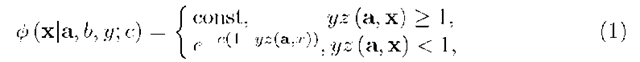 
And this distribution is defined by the objectively existing hyperplane
with an unknown directing vector of features
having a priori distribution
Using the maximum a posteriori probability principle for the directing vector parameters estimation (a, b) leads us to the widely-known support vector criterion
that was proposed by V. N. Vapnik from a strictly deterministic point of view. Of course, the concept of time is completely absent here.
The principal distinction of the
concept of non-stationary environment given in this paper consists in taking into consideration time factor t. We suppose that the main property of non-stationary environment is expressed by time-dependent separating hyperplane that characterizes primary difference of the feature vectors of instances of two classes. This separating hyperplane, in turn, is completely defined by its own direction vector and location parameter, which should be considered as time functions
In the terms of the improper probability distributions of two classes in the feature space such idea is formulated in the form of hypothesis that parameters of this pair of distributions are time varying:
where
We will suppose that at the zero time moment a priori distribution of the separating hyperplane is improper and has the appearance:
. In turn we will regard directing vector aj as a stochastic stationary process:
Dynamic Support Vector Machine Criterion
Now every instance
is considered only together with the indication of time point when this instance was presented
. As a result the training set represents as the set of triplet
a subset of instances, entered in time point t.
We obtain the sought-for sequence
as maximum point of joint a priori distribution of separating hyperplane’s parameters and training sample. The maximum a posteriori probability principle lets to the criterion
The criterion (4) realizes the conception of the rather smooth sequence of optimal separating hyperplanes as opposed to the conception of the single optimal hyperplane in (2).
As the classic learning problem, the dynamical problem (4) is a quadratic programming problem but contains T(n +1) + N variables in contrast to (n + 1)+N variables in (2). It is known that a computational complexity of the general quadratic programming problem is proportional to the cube of the number of variables, i.e. a dynamic problem ex facte is more complex than the classical problem.
But the objective function in a dynamic problem (4) is pair-wise separable, i.e. representing a sum of private functions every of which depends on the variables connected with one or two time points in their increasing order. The algorithm of the pair-wise separable criterion optimization suggested in this paper consists in an approximate implementation of the dynamic programming procedure and permits to solve the problem mentioned above within the number of iterations proportional to the length of the training sequence.
Quickly Optimization Procedure for a Dynamic SVM Criterion
The algorithm for the optimization of the obtained pair-wise separable criterion proposed in this paper is based on the using a general principle of the dynamic programming. Let us to introduce the following notation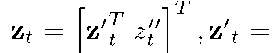
and rewrite the criterion (4) in a more convenient form
where the areas of acceptable values for variables are determined by the conditions
The central idea of the dynamical programming method uses the concept of a sequence of Bellman functions
con
The central idea of the dynamical programming method uses the concept of a sequence of Bellman functions
connected with partial criteria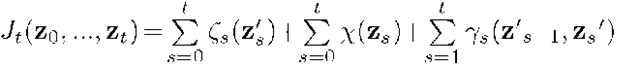
having the same structure as the full objective function but defined on the set of variables
In order to obtain the filtering estimations of the separating hyperplane’s parameters we will use the fundamental property of Bellman function
which is called the direct recurrence relation. The procedure begins with the first Bellman function
Then Bellman functions are recurrently evaluated for the following observation. And the minimum of Bellman function on every step determines the filtering value of the parameters of the optimal separating hyperplane
The optimization procedure is based on the hypothesis that there exists an appropriate compact form for Bellman functions representation, allowed to store this functions in the memory. But in the case then inequality constraints are imposed upon the sought-for variables and the Bellman functions are piecewise quadratic and consequently the dynamic programming procedure cannot be applied immediately. In order to save the computation advantages of the dynamic programming procedure we use here the following trick.
We heuristically replace the non quadratic functions
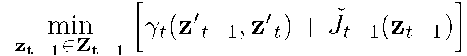by the some appropriate quadratic approximation
Then the following approximations of Bellman functions will be quadratic too and a numerical implementation of the dynamic programming procedure will be possible. Thus, the quadratic approximation of the Bellman function comes to the selection of appropriate values of the parameters
of the quadratic function
which would ensure invariance conservation of the main features of, generally speaking, non-quadratic function and consequently the initial Bellman function. Such features are the minimum point position
, minimum point value
, and also the matrix of the second derivatives at the minimum point
Case Study: Spam-Filtering Problem
The object of the experimental study in this paper is the problem of filtering spam-addresses in a result of retrieval request. The behavior of distributors of network advertising constantly improves and as a result a classifier of advertising links used by a search engine should adapt to the behavior of spammers. Consequently we come to problem of construction the time-dependent decision rule.
As the training data we took an anonymous set of hyperlinks URL Reputation Data Set from the repository UCI, first described in the paper [7]. This set consists of the addresses of Web resources for 121 days grouped according to the observation days and contains both advertising and relevant hyperlinks. Every instance in the data base is characterized by 3.2 million features which may be divided into two groups: lexical (hostname, primary domain, TLD and etc.) and host-based (WHOIS info, IP prefix, geographic and etc.). The values of features are normalized from 0 to 1, and the features themselves are anonymous. For carrying out the experiments from this data base in different ways there have been randomly selected 10 instances for each of 11 days taken from the 1st to the 110th day with the step of 10 days. The testing set was comprised by accidentally selected 4000 instances of the 120th day. We deleted the features with the values that are equal on all instances of the training set out of feature descriptions of the instances participating in the experiment, the number of the rest was 326. The experiment was repeated for different sets of training instances. Two algorithms were compared in the course of the experiment: normal support vector machine with the hyperplane, constructed on all instances of the training set and the algorithm of successive refinement of the decision rule, suggested in the paper. In the proposed algorithm of dynamic pattern recognition the parameters of the required decision rule d and d’ were chosen by cross-validation procedure, on each iteration of which non-stationary decision rule was constructed without taking into account the instances entered over one of the days. The general per cent of erroneously classified links e was calculated for each algorithm: the percent of malicious URLs erroneously classified as benign ones, and the per cent of benign URLs, erroneously classified as malicious ones e+. As the results given in the table show, the incremental learning algorithm of the pattern recognition allows to improve significantly the quality of recognition that indirectly confirms non-stationary character of the data used for the experiments.
|
Algorithm |
 |
 |
 |
|
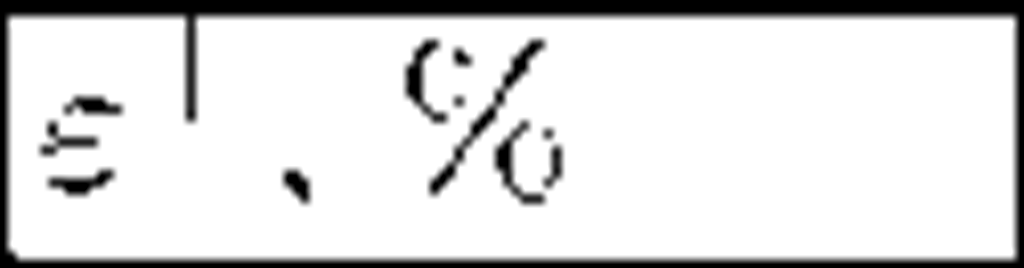SVM |
32.32 |
5.94 |
16.0 |
|
Incremental Algorithm |
14.96 |
4.49 |
8.49 |
Conclusions
In the paper the adaptation of the general definition of the pattern recognition learning problem with two classes of instances in the finite-dimensional space of real features is made under the conditions of non-stationary environment. The non-stationary property of environment is considered as time-changing decision rule. Under this assumption the learning criterion appeared a dynamic modification of SVM criterion. Also we have suggested optimization algorithm for Dynamic SVM having the linear computational complexity relative to the length of the training time series. Our algorithm was applied to the problem of filtering irrelevant or publicity hyperlinks as a result of retrieval request and its application achieved a good enough result as compared with classical SVM.
