Abstract
We exhibit an intimate connection between the concept of an annotated, ordered set and that of a pattern structure. This enables an exchange of ideas and techniques between both domains.
Introduction
Pattern structures were introduced in [KG01] to model information. The usefulness of annotated ordered sets for similar purposes was studied in [KSJ08]. Here, we compare and relate the two approaches. To keep the article rationably self-contained we recapitulate both concepts. We see how theorems can be moved between both domains and fix a theorem from [KG01].
In the first section we will introduce annotated ordered sets. In the second section we will outline pattern structures. In the third section we will argue that pattern structures can be understood as a certain sub-class of annotated ordered sets and review basic constructions and theorems. In the fourth section we will correct a theorem about pattern structures and their projections.
The reader is assumed to be knowledgeable about the basics of order theory and formal concept analysis as can be found in [DP90] and [GW99].
Annotated Ordered Sets
Annotated ordered sets were introduced to model taxonomies, e.g. appearing in the realm of the Gene Ontology.
Definition 1 ((elementary) annotated ordered set). Let
be a finite ordered set (poset), let X be a finite set of labels, and let
be an annotation function. Then we call
an annotated ordered set and refer to (X,F) as an annotation of P. In case P is a (complete) lattice we call
an annotated (complete) lattice denoted
. for convenience, we regard F as a map from X to P and say that
is elementary.
It is interesting to note that an annotated ordered set (P, X, F) can be regarded as a formal context with ordered attributes (X, P,Fr ) since every mapping 
can be interpreted as a relation
where xTRy if and only if
. But the concept lattice of this formal context would not yield the intended concept lattice representation of the annotated ordered set, since it does not express the semantics of annotation in a taxonomy, that is, if we annotate an example to a class in a taxonomy we implicitly mean that it belongs to all the super-classes of the class it was annotated to. Additionally, modelling the annotated taxonomy as formal context would be rather counter-intuitive.
We describe how an appropriate formal context can be derived from an annotated ordered set to produce its concept lattice representation. For an ordered set 
and node
we denote by
the principal filter of q and dually by
the principal ideal. Also, for later use, for
let
and dually
Given an annotated ordered set
we can construct a formal context
(X, P, I) where we define the relation
This means that I equals
. Note that in the case of an elementary annotated ordered set the definition of I can be written as
since F is regarded as mapping to P (instead of 2P).
The concept lattice of
will be denoted by
, where
is the set of formal concepts of the formal context
is called the concept lattice representation of the annotated ordered set
In case
forms an annotated complete lattice and
is a formal concept in
, we observe that
is the set of all
such that
is an upper bound of F(x). Also, for convenience, for a node
denote 
Pattern Structures
In [KG01] pattern structures are introduced to model information in the realm of pharmaceutical research. How pattern structures serve to analyze many-valued data contexts is described in [Ku09].
Definition 2 (pattern structure). Let G be a set, let
be a meet-semilattice, and let
Then
is called pattern structure 
generates a complete subsemilattice
The elements of G are called objects and the elements of D are called descriptions or patterns. The operation n models a similarity operation on the descriptions.
Pattern structures can be represented by the concept lattices of so called representation contexts. In the following we sketch the construction of representation contexts as given in [KG01]. First it is important to note that
is complete and therefore, there exists a (unique) operation U to make
into a complete lattice. This operation (on D) is given by
Furthermore, a subset M of D is called U-dense for
if any element
can be recaptured as join of elements
that is
Now (G, M, I) is a representation context for
if M is U-dense for (Dg, n) and
is defined as
Basic Connections
On the one hand, given an elementary annotated ordered set
we get a pattern structure
allows for (finite) meets and F (X) generates a complete subsemilattice of
On the other hand, given a pattern structure
we always get an elementary annotated ordered set
when considering the meet-semilattice as ordered set via the usual definition
Therefore, we see that pattern structures are special cases of annotated ordered sets and we can immediately transfer all results on annotated ordered sets to pattern structures. When we consider the other direction we must be more careful. But let us first compare the constructions of formal contexts for representation in both cases.
For the time being, let us consider a pattern structure
as elementary annotated ordered set and let us build its associated context via the annotated ordered sets method. We get
where
is given by
. It is obvious that D is
If we had dualized the order
upfront the above construction would have yielded a representation context for P. Therefore, we can conclude that the method for representation context construction for pattern structures generalizes the method for concept lattice representation for annotated ordered sets in this case. It is important to note that Theorem 1 in [KG01] implies that the concept lattices of (different) representation contexts for a given pattern structure are isomorphic.
In [KG01], it follows directly from Theorem 1 that
and the concept lattice of a representation context of the underlying pattern structure are anti-isomorphic. In the following, we exhibit a connection between the concept lattice of a representation context and D, the ordered set of all patterns. For elementary annotated complete lattices, Theorem 1 in [KSJ08] makes obvious that their concept lattice representations are tied to the underlying complete lattices via adjunctions. We need to generalize this result to pattern structures, since (D, C) is not necessarily a complete lattice.
Theorem 1. Let
be a pattern structure, let
be a representation context, let
be a mapping, and let
be a mapping. Then
forms a dual adjunction (or Galois connection) between the ordered set of patterns D and the concept lattice
. In particular, y is injective and is surjective.
Proof. We show that y is injective (the surjectivity of ^ follows from the injectivity of
). Assume we have two concepts (A, B) and (C, D) which are mapped to the same element, that is,
We will show that
from which it follows that
We have that
if and only if 
if and only if
for all
if and only if
The pair
forms a Galois connection since
From the above theorem it follows that the concept lattice of a representation context is embedded as a closure system into D.
In [KSJ08], it is investigated what can happen if we fix an ordered set and then vary the annotations. It turns out that the annotations are in one-to-one correspondence with the closure systems in the filter lattice of the ordered set. Clearly, this implies that in the case of pattern structures if a set of patterns or descriptions together with a similarity operation is given and we vary the annotation function 6 freely, we can only get a one-to-one correspondence between (elementary) annotations and a certain subset of the closure systems in the ideal lattice (the dual of the filter lattice of the ordered set). In the following we will single out this subset.
Theorem 2. Let G be a set of objects, and let
be a semi-lattice.
The elementary annotations are, up to annotational equivalence, in one-to-one correspondence to the principally generated closure systems in the ideal lattice of D.
Proof. Given an elementary annotation
every
is a principal ideal in
and an object intent of a formal concept of
Since, in general, the intents of all concepts of a formal context are exactly the meets of the object intents the annotation induces a principally generated closure system in the ideal lattice of D.
Given a closure system
in the ideal lattice of
generated by the principal ideals
we can define a corresponding elementary annotation 
where
Projections
For pattern structures so called projections where introduced in [KG01] to model the process of simplification of the underlying subsumption order. Projections are defined as kernel operators1 on the ordered set of patterns or descriptions. The existence of projections can be characterized by the existence of certain representation contexts. We quote Theorem 2 from [KG01]:
For pattern structures
the following two conditions are equivalent.
(1) There exists a projection
with
(2) There exist representation contexts (G, M, I) of
and
of
with
In the proof of the theorem it is claimed that
is a kernel operator on D if (G,N,I) is a representation context of (G, D,6). Examples 1 shows that condition (2) in Theorem 2 needs to be boosted 2 and Example 2 shows that the above operator used in the proof is not a kernel operator as claimed.
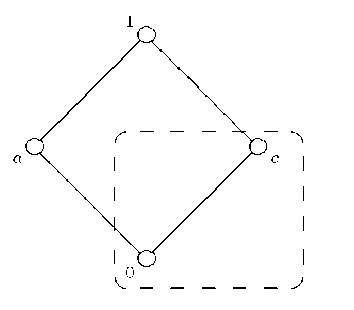
Example 1. Let D be given by the structure depicted in Figure 1 and let
(visualized by the dotted compartment in Figure 1) for i = 1, 2. Note that the carrier set
of the complete sub-semilattice generated by
is given by
for i =1, 2. It is immediate that
dense regarding
and that
, but obviously there exists no projection
with
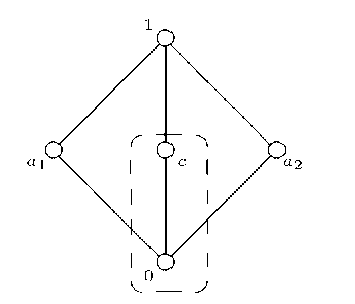
Fig. 1. (2) implies (1) does not hold in Theorem 2
Fig. 2. Operator from the proof is not a kernel operator
Example 2. Let D be given by the structure depicted in Figure 2 and let
and
(visualized by the dotted compartment in Figure 2). Note that the carrier set
of the complete sub-semilattice generated by 
is given by
It is immediate that M is U-dense regarding
but
is not contractive since
, thus
is not a kernel operator.
To repair Theorem 2 we additionally require that
is point-wise contained in 61 in condition (2) and to repair the proof we make the above operator into a kernel operator.
Theorem 3. For pattern structures
the following two conditions are equivalent.
(1) There exists a projection
with
(2) We have
and there exist representation contexts (G,M,I) of Pi and
Proof.
: Since there exists a projection
with
we have for
that
which implies
since
is contractive. We construct the two representation contexts. Let M := D and let
. Obviously, we have
. Since
we get
It remains to show that arbitrary meets of elements from
can be recovered from N.
