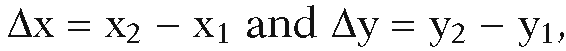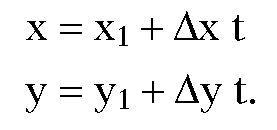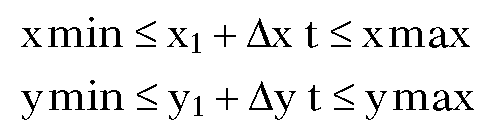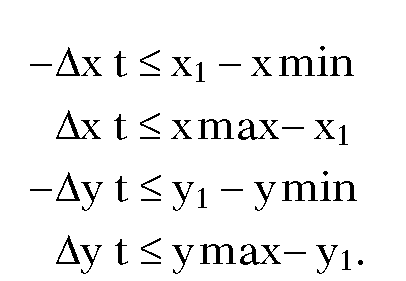Clipping (Basic Computer Graphics) Part 2

Liang-Barsky Line Clipping

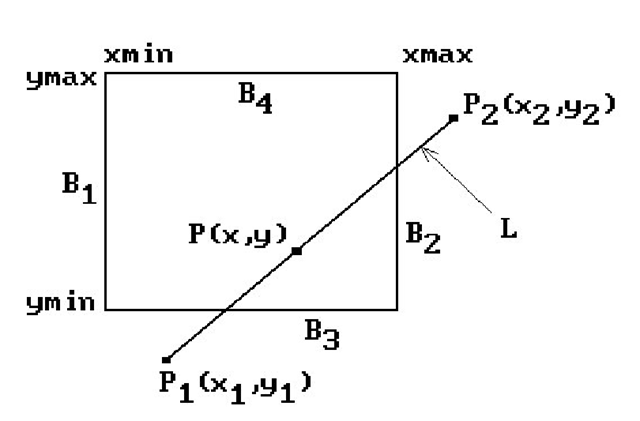
The Liang-Barsky line-clipping algorithm ([LiaB84]) optimizes the Cyrus-Beck line-clipping algorithm in the case where we are clipping against a rectangle. It starts by treating a segment as a parameterized set. LetA typical pointon    the oriented line L determined by P1 and P2 then has the form

See Figure 3.5. If we letthen

If the window W we are clipping against is the rectangle [xmin,xmax] x [ymin,ymax], then P belongs to W if and only if

that is,

 

 

Figure 3.5. Liang-Barsky line clipping.

To simplify the notation, we introduce variables ck and qk and rewrite these equations as

Set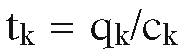whenever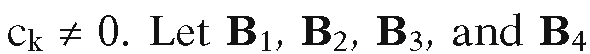denote the left, right, bottom, and top boundary lines of the window, respectively. With this notation we can make the following observations:

(1)    If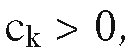then  L goes from the “inside” to the “outside” of the boundary line Bk as t increases and we shall call tk an exit value.

(2)    Ifthen  L goes from the “outside” to the “inside” of the boundary line Bk as t increases and we shall call tk an entry value.

(3)    Ifthe L is parallel to Bk, which is outside the window if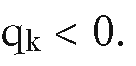

The clipping algorithm now proceeds by analyzing the three quantities qk, ck, and tk. Algorithm 3.2.3.1 is a high-level version of the Liang-Barsky algorithm. Algorithm 3.2.3.2 gives the code for the actual Liang-Barsky algorithm.

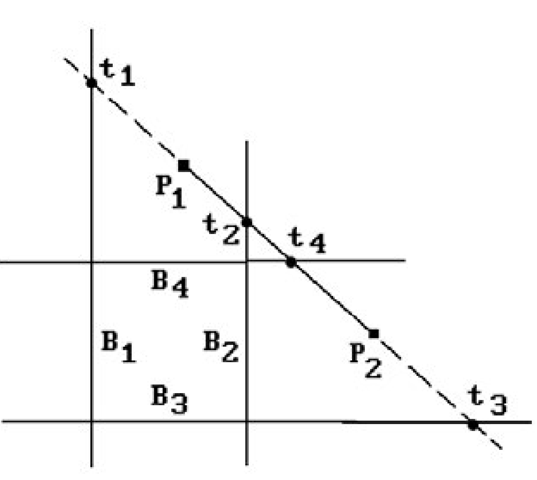
Example. Consider the segmentin    Figure 3.6. We  see that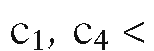 0 andIn    other    words,    t1 and t4 are entry values and t2 and t3 are exit values.

The picture bears this out. One can also easily see thatTherefore, there is an entry value (t4) that is larger than an exit value (t2). Using the algorithm we conclude that the segment lies entirely outside the window, which is correct.

Algorithm 3.2.3.1. High-level Liang-Barsky line-clipping algorithm.

Algorithm 3.2.3.2. The Liang-Barsky line-clipping algorithm.

Algorithm 3.2.3.2. The Liang-Barsky line-clipping algorithm.

Figure 3.6. Liang-Barsky line-clipping example.

Example. Consider the segment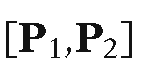in    Figure    3.7.    In    this    example, c1,

so that t1 and t3 are entry values and t2 and t4 are exit values. Furthermore,Thistime we cannot reject the segment and must compute t0 = maxThe    algorithm    tells us that we must clip the segment at the P1 end to get Q but do not need to clip at    the    P2 end. Again this is clearly what had to be done.

In conclusion, the advantage of the Liang-Barsky algorithm over the Cohen-Sutherland algorithm is that it involves less arithmetic and is therefore    faster.    It    needs only two subtractions to get qk and ck and then one division.

Figure 3.7. Liang-Barsky line-clipping example.