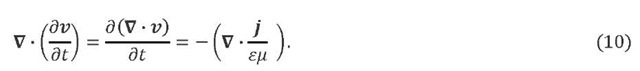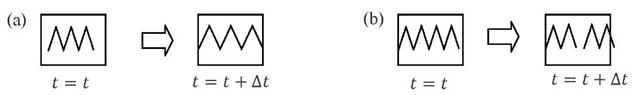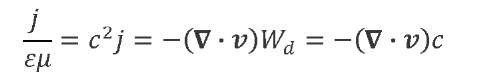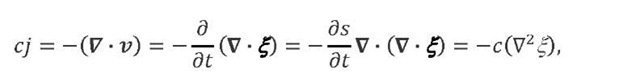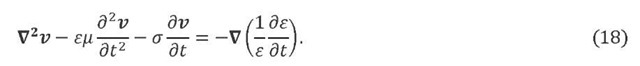ABSTRACT
Dynamics of deformation and fracture is considered based on a field theoretical approach. The basic postulate of this approach is that deformation is always locally linear elastic, and that the nonlinear behavior in the plastic regime can be formulated by considering the interaction of these local dynamics. By requesting that the transformation matrix representing the local elastic deformation is coordinate dependent so that it describes nonlinearity, and that the law of elasticity be invariant under the coordinate dependent transformation, this formalism introduces a compensating field known as the gauge field. By applying the Lagrangian formalism to the gauge field, the theory derives field equations that describe interaction between the translational and rotational modes of displacement. The plasticity is viewed as energy dissipating dynamics of the deformation charge, a quantity derived from the symmetry charge associated with the invariance of the elastic law. Recent analysis indicates that transition from plastic deformation to fracture is governed by the behavior of the deformation charge, and that an optical interfermetric technique known as the electronic speckle-pattern interferometry can be used to visualize the deformation charge.
Introduction
Deformation and fracture behavior observed in nano- and microscopic systems are substantially different from that observed in macroscopic systems. At the nanoscale, basic properties of material strength such as yield stress and flow stress of metals show strong size dependence. Fracture is initiated at the atomic scale, and develops to the final, macroscopic failure of the object. Understanding of deformation and fracture at the nanoscale is essential for full understanding of fracture at any scale level. Conventional theories of plastic deformation rely on experimentally determined constitutive relations and mathematical techniques for calculating non-uniform distributions of stress and strain [1, 2]; they are by nature phenomenological and dependent on the scale level that the experiment is conducted. It is extremely important to develop a scale independent theory.
Our approach is to describe the process of deformation and facture based on a fundamental physical principle known as local symmetry [3]. This approach is not only scale independent but also capable of describing all stages of deformation, from elastic deformation through fracture, on a common theoretical basis. The original idea to use local symmetry in the deformation dynamics was proposed by Panin et al [4] in the frame work of the general theory of deformation and fracture known as physical mesomechanics [5]. Essentially, the physical-mesomechanical formalism describes deformation by a linear transformation similar to that used by conventional continuum mechanics [6]. The nonlinearity in the plastic regime is described by allowing the transformation matrix to be coordinate-dependent, and requesting that the law of elasticity is invariant under the transformation. The aim of this paper is to focus on the physics aspect of the physical-mesomechanical formalism with some connection with dislocation dynamics. Supporting experimental data obtained with optical interferometry is also presented and discussed.
Formalism
Postulate
The basic postulate of the mesomechanical-approach is that when a material enters the plastic regime under the influence of external load, the deformation is still locally linear-elastic. This is reasonable because microscopically the internal force is proportional to displacement. In fact, most theories use inter-atomic potentials in the form of a quadratic function of the interatomic distance; basically they assume that the force is proportional to the displacement from the equilibrium. It is natural to assume that the conventional transformation matrix of elastic theory is locally applicable. The nonlinearity in the plastic regime is described through consideration of interaction among these local dynamics. As part of the same continuum material, all these local regions "know" how other regions are being deformed elastically at each moment. This interaction is conveniently integrated to the theory as a vector potential associated with a field [7, 8]. Mathematically, this field connects local regions and is called the connection field. In physics, it is called the gauge field, because it makes the local (gauge) dynamics invariant under the coordinate dependent transformation.
Field equation
Once the gauge field is identified, the so-called field equations can be derived by applying the least action principle. Detailed derivation is described in [7]. The field equations of the present dynamics can be given as follows.
Here the meaning of quantities appearing in eqs. (1) and (2) are as follows. v and o are the field variables of the gauge field, and are related to the temporal and spatial derivatives of the vector potential A as shown below1.
j0and j0 appearing on the right-hand side of eqs. (1) and (2) are the temporal and spatial components of the so-called charge of symmetry. c is the phase velocity of the spatiotemporal variation of the field [7]. From eqs. (3) and (4), it is found that v and o are related as follows.
Eq. (5) leads to the interpretation that v represents the average velocity of the unit volume at the coordinate point and o represents the rotation of the unit volume.
Substitution of eq. (5) to (2) leads a wave equation of the following form.
The general solution to eq. (6) represents decaying transverse waves. The phase velocity of a mechanical transverse wave is in general expressed as the square root of the ratio of shear modulus to the density. From this, e and 1 / n can be interpreted as the density and shear modulus of the material, and the phase velocity can be expressed as follows2.
Deformation charge and plasticity
The charge of symmetry appearing on the right-hand side of eq. (1) has a significant role in the deformation dynamics. From the law of mass conservation applied to a unit volume, the divergence of velocity field is equal to the temporal change in the density.
With the use of eq. (7), eq. (2) can be written in the following form.
Application of divergence to eq. (2) with the use of eq. (7) and the mathematical identity
leads to the following relation between charge
Eq. (10) can be viewed as an equation of continuity regarding
where
is the flow of
. This allows us to call 
the deformation charge, and j /n the current of the deformation charge putting it in the following form.
With eq. (8), j/n can further be written as
Here de /d t is the change in density over time. The current j / \i has a dimension of momentum change over time, or force, per unit volume.
Eq. (12) tells us that when the velocity field is diverging, the density of a unit volume affixed on the coordinate axis changes over time, and that the temporal change can be viewed as a drift of . However, it does not tell whether the deformation is elastic or plastic; whether a given deformation is elastic or plastic depends on how the density changes over time. Fig. 1 illustrates it schematically where the left picture represents the elastic case and the right the plastic case [8].
Fig. 1 Schematic illustration of one-dimensional V ■ v; (a) elastic case and (b) plastic case
When the deformation is elastic, the displacement field has longitudinal wave character; when a trough of the longitudinal wave (a peak of rarefaction) passes through a unit volume, the density of the volume increases at the next moment. From this viewpoint, it is natural to interpret that in the elastic case, the drift velocity represents the phase velocity of the longitudinal wave
(E: Young’s modulus). Substitution of
into eq. (11) leads to
hence,
and
Here % is the displacement,
Multiplication of
to the left-hand side and
to the right-hand side of eq. (13) leads to
With j / \i being the net force acting on the unit volume, the EV% appearing on the rightmost-hand side of eq. (15) can be interpreted as the field force at the boundary of the unit volume. Note that it is proportional to the Young’s modulus. When the displacement is characterized as a longitudinal wave of linear elasticity, the left-hand side of eq. (2) is zero [7, 9]. Under this condition, with eqs. (13) and (14), eq. (2) becomes
Eq. (16) is the well-known wave equation representing longitudinal elastic waves.
When the deformation is plastic, the temporal change in density associated with the divergence of the velocity field is due to dislocations, as Fig 1 illustrates; hence j /n represents a flow of dislocation. Since the change in density is due to the net flow into the unit volume, j /n is in the same direction as the total velocity of the point i.e., v, or Wd o v. So,
Being proportional to velocity, the longitudinal force j / n is by nature energy dissipating. With the use of eq. (17), eq. (6) can be written in the following form.
If the dislocation density rate is uniform and therefore the right-hand side of eq. (18) is small, the general solution to eq. (18) represents a decaying transverse wave. In a previous experimental study [10], clear decaying transverse wave characteristics have been observed in the displacement field of an aluminum alloy specimen under plastic deformation.
Ductility and fracture
With eq. (7) and rearrangement of the terms, eq. (2) can be rewritten as follows, which can be viewed as an equation of motion [11].
The left-hand side represents the change in momentum of the unit volume over time, equaling the net external force on the volume. The first term on the right-hand side represents the transverse restoring force due to the rotational deformation in proportion to the shear modulus . The second term on the right-hand side represents the longitudinal force acting on the unit volume. In the elastic regime, it represents the differential elastic force and in the plastic regime energy dissipating force as discussed above. Being the recovery force proportional to the rotational displacement, the first terms is the source of transverse wave characteristics in the plastic regime. As deformation develops, this term becomes less effective and instead the second term becomes more effective, causing decay of the wave. This idea can be naturally extended to fracture as the final stage where even the force due to the second term becomes zero.
According to eqs. (11) and (12), there are two ways to make j/n = 0; the first is V • v = 0 or de/dt = 0 , and the second is . The former represents the situation where the material cannot create dislocation anymore via divergence in the velocity field. The second is the situation where the location where divergence in velocity cannot move, and consequently the material keeps increasing strain concentration at the same spot, or in other words, the same spot keeps losing the density. Naturally, this leads to discontinuity of the material or fracture.
Experimental
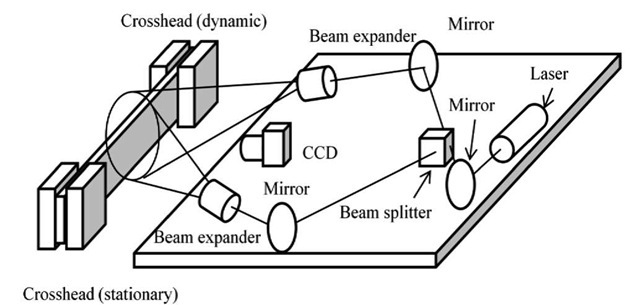
A number of experiments [9-12] have been conducted with the use of an optical interferometric technique known as the ESPI (Electronic Speckle-pattern Intrerferometry). Fig. 2 illustrates a typical ESPI setup. The laser beam (helium-neon laser oscillating at 632.8 nm) is split into two horizontal interferometric paths that are recombined on the specimen’s surface aft er being expanded by beam expanders. The interferometric image of the specimen is captured by the CCD (charge coup-led device) camera at a constant frame rate (typically 30 frames/s), and the digital images are transferred to computer memory. Fringe patterns containing the in-plane displacement are generated via subtraction of a frame taken at a certain time step from a frame taken another time step.
Fig. 2 Typical ESPI optical setup for deformation study
Fig. 3 shows typical subtraction fringe patterns obtained in a tensile experiment on a 0.5 mm-thick aluminum alloy specimen (25 mm x 4 mm in gauge length) under constant pulling speed of 20 |im/s. The left three patterns [(a-1)-(a-3)] are formed in an early stage of plastic regime and the right three [(b-1)-(b-3)] are in the final stage of deformation. Bright band patterns are seen at various locations. Detailed studies [8, 11, 13] on this pattern indicate that it represents concentrated normal strain and considered to be representing the deformation charge defined in conjunction with its current given by eq. (11). Notice that Fig. 3 indicates that in the early stage, the deformation charge is dynamic (it changes the locations to appear), but in the late stage it tends to be stationary at a spot where the specimen eventually fractures. This observation clearly supports the above argument on the final stage of deformation where the drift velocity Wd becoming null.
Fig. 3 Fringe patterns showing bright patterns presumably representing deformation charges
Also interesting to note in Fig. 3 is that the bright band appearing near the upper end of the specimen in Fig. 3 (a-3) has curvature whose radial direction seems to be parallel to the change in the width of the specimen toward the upper end. This indicates that the bright band representing the deformation charge is drifting in the direction of the local displacement whose pattern of stream lines diverge upward as the specimen becomes wider. A similar observation that the pattern considered to be representing the deformation charge seemingly drift in the direction of displacement in an tensile experiment of a notched specimen3.
Summary
Dynamics of deformation has been discussed from the viewpoint of a field theoretical approach based on gauge invariance. The deformation charge has identified as a quantity that causes energy dissipation and hence irreversible deformation in the plastic regime. It also plays a significant role in the transition from late plastic deformation to fracture. The ESPI technique has been described as a powerful experimental method to investigate deformation and fracture based on the theoretical approach discussed in this paper.
