ABSTRACT
The double cleavage drilled compression (DCDC) fracture test uses axial compression to drive stable cracks in glasses and brittle polymers. The cracks are generated by regions of tension in a rectangular column of material containing a central hole. The observed relationship between crack length and the applied axial stress is fitted with a two-dimensional finite element model to estimate fracture toughness. The model is applied to previous DCDC experimental results for poly(methyl methacrylate) (PMMA) samples of varying thicknesses. Both plane stress and plane strain cases are considered. Three dimensional finite element models of the DCDC test indicate plane stress analysis is the most applicable condition and suggest explanations for the effect of sample thickness.
Keywords: DCDC, PMMA, fracture, healing, toughness, finite element
INTRODUCTION
The double cleavage drilled compression (DCDC) fracture test uses uniaxial compression to generate large cracks in a brittle material [1]. The DCDC sample is a tall, rectangular column with a central, through-thickness hole (Figure 1a). Under compression, regions of tension at the apex and base of the hole create and propagate symmetric mode I cracks. The length of the cracks is controlled by the axial compression. Several models have been proposed to correlate the relationship between applied stress and crack length with fracture toughness, a quantitative measure of the material’s resistance to fracture.
The influence of DCDC sample height, width, and hole size on the observed fracture behavior has been previously studied and factored into proposed fracture toughness models [2]. Here, we examine our DCDC experiments on samples with different thicknesses, noting the thicker samples require more stress to propagate long cracks. We use two- and three-dimensional finite element calculations to investigate this thickness effect.
EXPERIMENTAL
DCDC tests were conducted on poly(methyl methacrylate) (PMMA) samples with thicknesses of 3, 4, 5, 8, and 11 mm [3]. The samples were 50 mm tall and 12 mm wide with a 3 mm diameter central hole. The thinnest samples (3, 4, and 5 mm) were loosely fitted with a brace to prevent out-of-plane buckling. After initiating the cracks, uniaxial compression was applied under displacement control at 0.5 ^m/sec. The crack length was measured every 30 seconds and correlated with the applied load. Increasing sample thickness was found to increase the axial stress required to propagate long cracks (cracks longer than the diameter of the hole).
COMPUTATIONAL
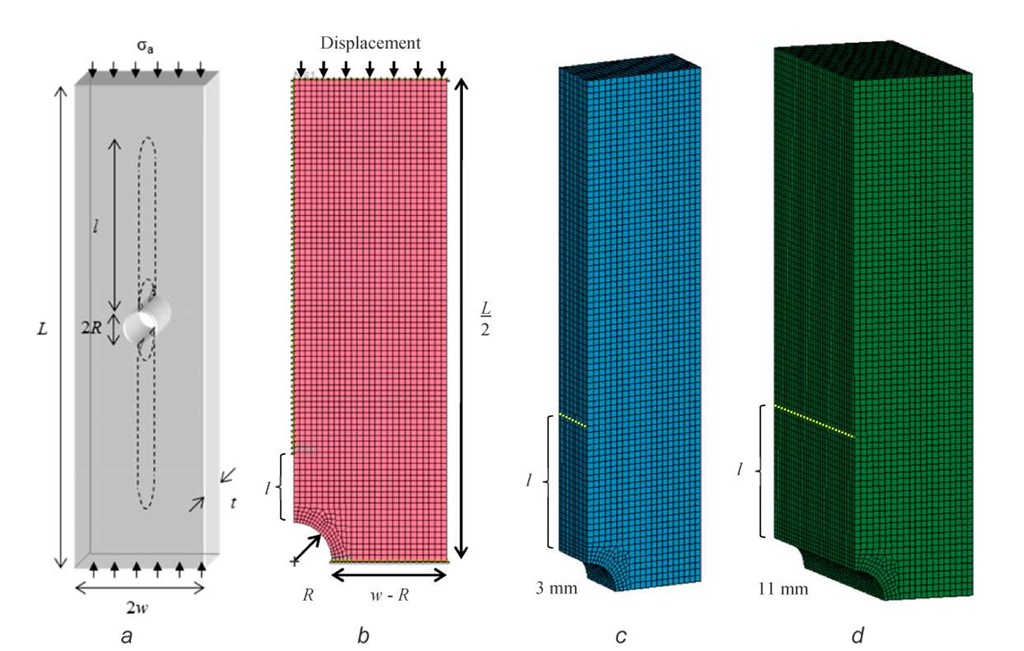
A two-dimensional finite element calculation was developed [3] to estimate PMMA fracture toughness using the DCDC experimental data. One quarter of the DCDC geometry was modeled with shell elements and a linear elastic material model (Figure 1b). The boundary conditions were correlated with experimental observations (applied force and crack length). Extending the crack in the calculation yielded a change in internal energy, an energy release rate, and a critical stress intensity factor.
Figure 1. (a) DCDC geometry. (b) 2D finite element model. (c) 3D 3 mm thick finite element model. (d) 3D 11 mm thick finite element model.
Plane stress and plane strain conditions in this 2D calculation were compared as an approximation of the effect of thickness. The pronounced thumbnail shape of the cracks in the thicker samples suggested an internal stress state closer to plane strain. It was initially assumed that plane strain and plane stress represent the extreme cases of thick and thin DCDC geometries. The calculations, however, do not indicate a significant difference in axial stress at the same crack opening stress between plane stress and plane strain cases.
New, three-dimensional finite element models were developed to better study the influence of sample thickness on the DCDC test. The 3 and 11 mm geometries were modeled (Figures 1c and 1d) following a similar approach to the 2D case, although the crack lengths were fixed at twice the hole diameter. The results show that the samples are generally in plane stress in both cases, and the thumbnail crack tip shape is due to localized variations in the stress state. Out-of-plane tensile stresses were observed in both geometries, an effect not captured by the 2D calculations. At the same average crack opening stress along the crack tip, the 11 mm thick geometry required more axial stress than the 3 mm thick geometry. The increase in axial stress is less than half of the difference observed experimentally, but the discrepancy can be attributed to simplifying assumptions, including a linear elastic material model, straight crack tip, and unconcentrated mesh at the crack tip.
CONCLUSIONS
Double cleavage drilled compression (DCDC) fracture tests of PMMA show thicker samples require more axial stress to propagate long cracks. Two-dimensional finite element calculations using plane strain and plane stress assumptions do not identify the reason. Three-dimensional finite element calculations yield out-of-plane tensile stresses and higher axial stresses for thicker samples. These results indicate that increasing DCDC sample thickness increases the overall constraint on the deformation of the sample. This constraint necessitates more axial stress to propagate the cracks.