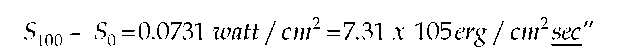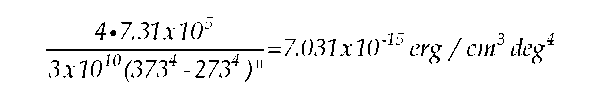Introduction
A new foundational physics is emerging which radically changes our concepts of electromagnetic waves. The original quantum ideas of Max Planck and Albert Einstein from the turn of the twentieth century, are undergoing an impressive renaissance now at the turn of the twenty-first century. The result is a fundamental physics of electromagnetic waves that is both new and classical. Einstein’s insistence that quantum mechanics was incomplete – that "hidden variables" were yet to be discovered – was correct. The recent discovery of those variables is the driving force behind this rebirth of the foundations of quantum mechanics and the fundamental physics of electromagnetic ("EM") waves. The new quantum variables have led to the discovery of new universal constants for EM waves. The new constants have revealed an elegant simplicity in quantum concepts, that requires no paradoxical explanations and imposes no uncertainties or limits. Instead, the new physics provides a more realistic understanding of physical concepts related to EM waves. The old paradigm is disappearing, and yielding to a new paradigm which is both more understandable and more powerful.
Background
It is often said that to successfully navigate the future one must understand the past. The fundamental physics of electromagnetic waves are no exception to this wisdom. In fact, an understanding of the origins of 20th century physics regarding electromagnetic waves is of vital importance to understanding the scientific revolution that is currently taking place.
Physics in the ages of reason and enlightenment
Galileo Galilei (1564 – 1642) was one of the most influential scientists of the millennium, however he lived during a time when the protestant reformation was gaining momentum and Europe was in turmoil. The Catholic Church was losing its hold on much of northern Europe and the Thirty Years’ War raged. Galileo resided on the Italian peninsula, where the Church maintained a strong hold, and he could not rely on the protection of reformers in other parts of Europe. None-the-less, even though "pagan" beliefs associated with frequency and resonance-related phenomena had been banned by the Church for centuries, Galileo performed research on natural resonant frequencies in a pendulum system. (Mortenson, 2010b).
In 1632, Galileo published his "Dialogue" and in a daring move described the mechanics of natural resonant frequencies writing, "the Pendulum makes its vibrations with one and the same frequency" and "every Pendulum hath the Time of its Vibrations…pre-fixed…[and] it is impossible to make it move under any other Period, than that …which is natural unto it." (Galilei, 1632) He described the resonant accelerating forces produced by precisely time puffs of his breath stating, "by blowing upon [the Pendulum one may] confer a Motion, and a Motion considerably great by reiterating the blasts, but only under the Time properly belonging to its Vibrations". Galileo thus provided one of the first documented descriptions of resonance, namely the increase in amplitude and energy of a system’s vibrations when an applied vibration, motion or energy matches the natural frequency of the system. Unfortunately, the Church was less accommodating than Galileo had anticipated. He was convicted of heresy and placed under house arrest for the rest of his life.
Pierre de Fermat (1601 – 1665) was a French attorney who was in his mid-thirties when Galileo was accused of heresy. Although Fermat’s personal passion was mathematics, he was well aware that pursuit of certain mathematical subjects could be very dangerous. Thus Fermat engaged in his passion in secret, scribbling notes in the margins of topics in his private library. One set of notes was a resonance equation, demonstrating that as the rate of a mechanical vibration (e.g., a puff of breath) neared the natural vibratory rate of a body (e.g., the swing of a pendulum), the amplitude of vibrations in the body increased (also see Figure 1., below):
Fig. 1. Fermat’s resonance curve showing an increase in vibration amplitude when forces are applied at natural resonant frequencies ("vr").
The brilliant young Isaac Newton (1643 – 1727) wrote his famous Principia, describing his three (3) laws of motion around the time of Fermat’s death. (Newton, 1898) The religious climate in England was quite chaotic at the time, and Newton waited another twenty (20) years to actually publish his Principia. His second law (force equals mass times acceleration) provided the basis for yet another resonance equation:
where "A" is the amplitude of the system’s oscillations, "a" is the acceleration in the system’s oscillation (caused in Galileo’s case by the force of his small puffs of breath), "vr" is the resonant or natural frequency of the system, and "vo" is the frequency of the outside force applied to the system. As this second resonance equation shows, an outside force applied at a frequency which is either much higher or much lower than the natural resonant frequency of the system, produces a large denominator and hence a small amplitude. Conversely, the closer the frequency of the outside force is to the resonant natural frequency, the smaller the denominator becomes. Very large amplitudes are produced. When the outside frequency exactly matches the resonant frequency of the system the amplitude is theoretically infinite (Figure 2.).
Fig. 2. Graphical representation of resonant amplitude equation (Eq. 2). The resonant frequency "vr" is at the origin, and input frequency of the outside force "vo" varies. As the input frequency approaches the resonant frequency, amplitude approaches infinity.
Newton distinguished the force exerted by an accelerating body, from the energy of a body simply in motion (which he referred to as vis viva) the product of mass and velocity:
where "m" is mass and "v" is velocity. This led to the great vis viva controversy several decades later (see below). By 1704 Newton had published his treatise "Opticks" in which he proposed the corpuscular theory of light, namely that light is composed of tiny particles that travel in straight lines. In a foreshadowing of Einstein’s later work, Newton stated, "Are not gross Bodies and Light convertible into one another, …and may not Bodies receive much of their Activity from the Particles of Light which enter their Composition?"
A few decades later the great vis viva controversy erupted with Giovanni Poleni’s (16831761) proposal that vis viva energy was proportional to the product of mass and velocity squared, putting him at odds with Newton. The debate was soon joined by Leibnitz, Huygens, and others. Dutch physicist Willem Gravesande (1688 -1742) performed meticulous experiments and concluded that energy of motion, "follow[s] the Ratio compounded of the Masses, and the Squares of the Velocities" (underline added).
Nineteenth century physics
By the nineteenth century, the brilliant Joseph Louis Lagrange (1736 – 1813) had organized the works of nearly every known scientist on matters of velocity, inertia, force, energy, and dynamics into his "Mechanique Analytique". (Lagrange, 1811) Lagrange declared that for a body at constant velocity, its energy (vis viva) was equal to "mv2", resulting "solely from the inertia forces of the bodies". Conversely, the energy required to accelerate a body was a function of the distance over which a force acted "F 8s". Lagrange explained that all systems exhibited a dynamic equilibrium between the vis viva of constant velocity and the forces of acceleration, "The sum of these two quantities, when equated to zero, constitutes the general formula of dynamics… when the equilibrium does not hold, the bodies must necessarily move due to all or some of the forces which act on them." For purposes of systematically explaining analytic mechanics Lagrange stated that he had assumed that an acceleration always occurs in a time period at least as long as the unit time for velocity. His assumption effectively fixed the acceleration time interval at "one second" and excluded accelerations taking place in less than one second.
Lagrange also addressed resonance dynamics using a mathematical function: "in the case where the same function is a maximum, the equilibrium will not be stable and once disturbed the system will begin by performing fairly small oscillations but the amplitude of the [resonant] oscillation will continually grow larger." He included additional sections on "harmonics [at the] nodes of vibration", "the resonance of a sonorous body", and the resonance dynamics of pendulum oscillations.
Forty years later, Gaspard-Gustave de Coriolis (1792-1843) borrowed heavily from Lagrange’s work in his popular engineering textbook. (Coriolis, 1829) Coriolis adopted Lagrange’s assumption regarding the acceleration time interval for simplicity’s sake, and explicitly explained that this assumption excluded consideration of "instantaneous" effects. Without the assumption, separate time variables for velocity and acceleration would have been required. Coriolis also introduced the concept of kinetic energy as a convenience in engineering applications involving gravitational effects: "the mass times one-half the square of the speed [Vimv2].. .will introduce more simplicity.since the factor nh(v2/g)’ is nothing more than the height from which a heavy body.must fall so that it may acquire the speed ‘v’". Acutely aware that his kinetic energy formula did not apply to objects moving at constant velocity, Coriolis wrote that when "the speeds have become the same… [the kinetic energy] becom[es] zero". Coriolis’ caveats were soon forgotten, however. By the time James Clerk Maxwell (18311879) later wrote his basic physics textbook, he errantly summarized, "The kinetic energy of a body is the energy it has in virtue of being in motion…"
Meanwhile, the interdisciplinary scientist Thomas Young, M.D., (1773 – 1829) began publishing physics articles anonymously (to protect the reputation of his medical practice). He eventually went public, and according to Young his greatest scientific achievement was establishment of the wave theory of light, based on his double slit experiment. Published exactly 100 years after Newton’s Opticks, Young’s reports on the wave-like interference of light eventually resulted in abandonment of Newton’s light corpuscle theory. This led to development of the belief that matter was composed of small particles, and light composed of continuous waves.
Another interdisciplinary scientist – Hermann von Helmholtz, M.D., (1821 – 1894) – was an army surgeon who set up energy-related experiments on frogs in his army barracks. Those same biomechanical experiments led to his great treatise on the transformation and conservation of energy. (Helmholtz, 1889) Helmholtz’s work on conservation of energy became the first law of thermodynamics, namely that energy is neither created nor destroyed, but is instead conserved and transformed from one form to another, "…heat, electricity, magnetism, light, and chemical affinity … from each of these different manifestations of [energy] we can set every other [manifestation] in motion". Helmholtz carefully differentiated between orderly work energy and disorderly thermal energy, and taught that the total energy of a system was their sum:
where "U" is the internal energy of a system, "A" the work (Helmholtz) energy, "T" temperature, "S" entropy, and the product "TS" thermal energy.
Helmholtz also wrote extensively about resonance which is, "always found in those bodies which when once set in motion by any impulse, continue to perform a long series of vibrations before they come to rest… provided the periodic time of the gentle blows is precisely the same as the periodic time of the body’s own vibrations, very large and powerful oscillations may result. But if the periodic time of the regular blows is different from the periodic time of the oscillations, the resulting motion will be weak or quite insensible." (Helmholtz, 1862) He also described resonant coupling as "sympathetic resonance". Helmholtz eventually rose to the highest physics position in Germany at the University of Berlin, where he influenced many young students including Max Planck (1858 – 1947) and Heinrich Hertz (1857 – 1894). (Helmholtz, 1896 and 1904) After Helmholtz challenged Hertz to prove the existence of Maxwell’s theoretical EM waves, Hertz succeeded brilliantly. The new EM waves were called "resonant Hertzian waves", based on the resonant electrical processes Hertz used to transmit and receive them.
The quantum revolution
By the late 1800′s, the young Max Planck was himself a professor at the University of Berlin and was doing theoretical work on Hertz’s electromagnetic waves. (Planck 1896 and 1897) Planck modeled the EM waves on the one hand as resonant waves capable of producing orderly work energy "A", and on the other hand as EM waves produced by random chaotic motions based solely on temperature "TS" (blackbody radiation). (Planck, 1900) Late in 1900 Planck met with success regarding the random thermal EM waves when he empirically determined the correct formula for blackbody radiation. A proper derivation of that empirical equation, however, was another matter altogether and according to Planck was the hardest work of his life. (Planck, 1901 and 1920)
Planck started with the Helmholtz equation (U = A + TS) and then introduced his non-controversial resonance hypothesis: EM "resonant Hertzian waves" are orderly and are thus completely free to be converted into work, and thereby constitute work energy, "A". Planck next explained that, because the blackbody apparatus used in the laboratory had been specifically designed to exclude all resonant EM waves, he could assume there was no work energy in the blackbody device. According to Planck, "A" equaled zero, and thus "the entire problem is reduced to determining S as a function of U". He borrowed Wilhelm Wien’s method of solving for energy density (which eliminated a time variable) and also eventually resorted to the statistical methods of his arch nemesis, Ludwig Boltzmann (1844 – 1906). Boltzmann’s kinetic mechanics were based on the limiting assumption that all the elements (e.g., molecules or atoms) in a system were moving randomly, in a completely disordered manner. Boltzmann’s mechanics were restricted to the thermal energy portion, "TS", of Helmholtz’s energy equation and could not be applied to orderly work energy, "A". The blackbody device and experiments were deliberately designed to exclude work energy and measure only disorderly, chaotic thermal energy, however. This fact allowed Planck to use Boltzmann’s statistical methods in his blackbody derivation, and "determin[e] S [solely] as a function of U". It also required however, that Planck introduce his quantum hypothesis -namely, that energy is quantized in small uniform amounts. Significantly, Planck assumed that those small uniform amounts of energy were different for each frequency, creating an a priori limitation which excluded consideration of a unit of energy for EM waves, analogous to the unit of charge for electrons. Mathematically Planck’s quantum hypothesis took the form of the quantum formula which Planck assumed as a given:
where "h" is Planck’s action constant, 6.626 X 10-34 Joule seconds.
Planck also calculated a thermodynamic constant, now called the Boltzmann constant:
where "E" is the energy of a single element (e.g., a single atom or molecule) based solely on its temperature "T", and "kB" is the Boltzmann constant, 1.38 x10-23 Joules per degree K per element. Just as Helmholtz’s equation provided the energy of a macroscale system based on its temperature ("TS"), Planck’s thermodynamic equation provided the energy of an individual microscale element based on its temperature ("kBT"). Thus, the Boltzmann constant is the microscale equivalent of entropy. Planck never introduced a microscale equivalent of the work energy "A", however: the blackbody experiments excluded work energy. This resulted in a microscale energy formula which was necessarily incomplete for any system in which work energy was present.
While some scientists used Planck’s blackbody equation for practical applications, his revolutionary quantum hypothesis received little attention – until, that is, Albert Einstein’s (1879 – 1955) own revolutionary papers were published in 1905. (Einstein, 1905) Einstein had seized on Planck’s quantum hypothesis and used it to provide explanations for a number of unexplained phenomena such as the photoelectric effect and ionization of gases. The interactions of EM waves and matter, he proposed, "appear more readily understood if one assumes that the energy of light is discontinuously distributed in space", e.g., in small particles or packets along the lines of Newton’s "light corpuscles", and is absorbed in "complete units" or "quanta".
Although highly controversial, Einstein’s papers brought attention to Planck’s quantum hypothesis and formula. A few years later, Niels Bohr (1885 – 1962) adopted Planck’s quantum formula in his theory of the hydrogen atom. (Bohr, 1913) Controversy still raged however, and Robert Millikan (1858 – 1963) undertook a series of meticulous experiments testing the validity of Planck’s constant and what he described as Einstein’s "reckless" theories regarding energy quanta and photoelectric phenomena. (Millikan, 1916) Millikan, well familiar with Planck’s accepted resonance hypothesis distinguished the photoelectric effect as an ordered work function and not a thermal effect: "photoelectrons do not share in the energies of thermal agitation.. .absorption [of EM waves] is due to resonance (and we know of no other way in which to conceive it.)". Echoing Galileo, Millikan stated, "the phenomena of absorption and of emission show that.. .oscillators possess natural frequencies.and the characteristic waves which they emit are of these frequencies.. .if any particular frequency is incident upon such a substance the oscillators in it which are in tune with the impressed waves may be assumed to absorb the incident waves". Regarding the resonant work nature of the photoelectric effect he stated, "emission of [electrons] from the atom.takes place especially copiously when the impressed frequency coincides with a ‘natural frequency’… [It] furnishes a proof which is quite independent of the facts of black-body [thermal] radiation, of the correctness of the fundamental assumption of the quantum theory, namely, the assumption of a discontinuous.. .energy absorbed by the electronic constituents of atoms from [EM] waves". (Underline added) The quantum revolution begun by Planck and Einstein was taking hold.
The quantum paradox
As the quantum revolution began to gain momentum, paradoxes and puzzles began cropping up. The simple model of light waves and matter particles had been disrupted. Louis de Broglie (1892 – 1987) added to the confusion in the early 1920′s when he proposed that if light could be both a wave and a particle, then so could matter. (de Broglie, 1924) Pursuing that line of reasoning, de Broglie found the lack of a unit of energy for EM waves, i.e., "an isolated quantity of energy" particularly troublesome. Without an energy constant for light (i.e., an isolated quantity of energy), de Broglie was unable to determine the fundamental mass of light using Einstein’s energy-mass equivalence equation, "E = mc2". Instead, the energy of light paradoxically depended on its frequency. De Broglie made the best of a conceptually difficult situation, and instead set Einstein’s mass equivalence equation equal to Planck’s quantum formula and solved for the rest mass of light at a particular frequency:
where "m0" is the rest mass of light, and "c" the speed of light in vacuo. Since the number of different frequencies of EM waves are theoretically infinite, this approach produced a paradoxically infinite number of values for the rest mass of light. Unlike other particles such as the electron or proton, de Broglie could find no constant rest mass associated with light particles.
The lack of any energy or mass constants for light was quite puzzling indeed. Unbeknownst to de Broglie, Planck’s limiting assumption about different quanta for each frequency excluded the very unit quantity of energy de Broglie sought. De Broglie could at least conclude however, that the rest mass of light in the visible region was quite small and in his Nobel prize speech explained, "The general formulae. may be applied to corpuscles of [visible] light on the assumption that here the rest mass m0 is infinitely small… the upper limit of m0 … is approximately 10-24 gram. (de Broglie, 1929)
De Broglie also used Planck’s quantum formula to derive the momentum for light:
finding that the momentum of light appeared to be directly proportional to its frequency, and thus inversely proportional to its wavelength "A". Once again, De Broglie obtained a zoo of values – this time for momentum since the range of frequencies and wavelengths in the EM spectrum is infinite.
In the meantime, Neils Bohr undertook his ambitious project modeling the hydrogen atom based on Planck’s quantum formula and constant. Bohr found that he could not calculate time intervals in regard to the interactions between EM waves and electrons. He was forced to model instantaneously "jumping electrons" instead. (Bohr, 1913 and 1920) Few (including Bohr) were satisfied with the jumping electrons however, and in the mid-1920′s two new approaches to quantum mechanics were introduced. In 1925, Werner Heisenberg, introduced matrix mechanics. (Heisenberg, 1925) A year later Erwin Schrodinger began publishing a series of papers on wave equations, intended to represent the real electron waves suggested by de Broglie. (Schrodinger, 1982)
Even with these two new approaches quantum mechanics still did not make sense to many early quantum pioneers. It lacked the certainty and definiteness of classical mechanics. Efforts to compensate for the many paradoxes included additional principles such as Heisenberg’s uncertainty principle, and Bohr’s complementarity principle. (Heisenberg, 1920 and Bohr, 1928) Additional variables and constants of inexplicable origin were discovered, such as the dimensionless fine structure constant. Discussion and debates continued. The Bohr-Heisenberg school of probabilities and uncertainty battled the Einstein – Schrodinger school of realism and certainty. Without answers for such simple matters as an energy constant or rest mass for light, the Bohr-Heisenberg school eventually prevailed. Scientists concluded (over Schrodinger’s strenuous objections) that his wave equations represented only probabilities, and not real physical waves. The consensus that finally emerged was that the classical mechanics of our macroscale world simply could not be applied to the kaleidoscopic microscale world of the quantum. According to Bohr, a classical limit existed at the very highest electron energy levels in atoms, and below that limit classical mechanics simply could not be applied.
The iconoclastic brilliance which initially led Einstein to make his "reckless" quantum proposals, would not allow him to join the quantum crowd and he insisted that something had been missed. He simply could not believe that God and the universe were so perversely paradoxical. In 1935, Einstein published his "EPR" paper loudly proclaiming that quantum mechanics was incomplete due to the existence of "hidden" quantum variables. (Einstein, 1935) Einstein and others such as Bohm and Bell tried to describe the hidden variables, but such a task was difficult, if not impossible. (Bohm, 1952) How does one describe a quantum variable mathematically, when the very nature of the variable is unknown? Small groups of scientists have attempted to keep Einstein’s quest alive, but the scientific community as a whole abandoned efforts to find any "hidden variables". Instead, it was generally agreed that the paradoxical nature of quantum mechanics was an undeniable reality of life. Incredible efforts then went into developing more quantum models incorporating the paradoxes, such as theories of strings, super-symmetry, membranes, and the like.
Einstein’s stubborn insistence that something had been missed was correct, however. The first of his "hidden variables" was discovered nearly a century later, the result of a small mathematical thread. (Brooks, 2009,a) Tracing that thread through the historical record, it led to the discovery that a minor mathematical inadvertence in Planck’s brilliant blackbody work had induced him to assume an incomplete and abbreviated version of the full quantum formula. All of quantum physics was based on Planck’s simple quantum formula, and that assumed formula was incomplete: it was missing a time variable. After restoring the time variable, Planck’s constant took on new fundamental meaning. The rich quantum tapestry that emerged, revealed beautifully symmetric quantum principles grounded in reality and certainty, using the complete quantum formula and a more inclusive or complete "thermo"dynamic formula. (Brooks, 2009,b)
The complete quantum formula
The complete quantum formula is:
where "h" is the energy constant for light (6.626 X 10-34 Joules/oscillation) and "tm" is the measurement time variable.
The time variable
The complete quantum formula is quite similar to an energy relationship found in Planck’s early theoretical electromagnetic work from the late 1890′s. He converted time-based power measurements, "E/1", to total energy values by multiplying by the measurement time, "tm". Planck’s EM theory used that simple conversion in a generic relationship in which the oscillation energy of a system was proportional to the product of a generic constant "a", the measurement time variable, and frequency:
A few years later, the time variable was lost in Planck’s complicated blackbody derivation. Instead of multiplying time-based energy measurements by the measurement time, Planck adopted Wien’s mathematical methods which converted the power measurements into energy density values by dividing by the speed of light. This caused the measurement time variable "8tm" to be simultaneously fixed at a value of "one second", and then "hidden". Proof of these facts are found in Planck’s 1901 blackbody paper, in which he described the experimental data and mathematical methods he used:
"§11. The values of both universal constants h and k may be calculated rather precisely with the aid of available measurement. F. Kurlbaum, designating the total energy radiating into air from 1 sq cm of a black body at temperature t° C in 1 sec, by St found that:
Instead of multiplying Kurlbaum’s time-based power measurement by the measurement time to obtain total energy (as Planck had done in his earlier work), he converted the power measurement to energy density by dividing by the speed of light "c" (3 X 1010 cm/ sec), according to Wien’s method:
"From this one can obtain the energy density of the total radiation energy in air at the absolute temperature
The time variables in the numerator and denominator cancelled out and Planck was seemingly able to address energy independent of time. Dividing by the constant speed of light however, is the same as multiplying by time:
where "s" is distance. In this case the time value by which the power measurement was multiplied was the constant "one second" unit time of the constant speed of light. Planck seems to have been unaware that by using Wien’s energy density calculation he was actually causing the infinitely variable measurement time to be fixed at a constant value of one second. He also seems to have been unaware that the fixed time variable was subsequently hidden in the final calculations of his action constant "h":
His action constant is actually the product of a true universal constant – " h " – and the fixed, hidden measurement time variable, "tm".
The energy constant
When the missing time variable is restored to the quantum formula, the identity of Planck’s real universal constant becomes apparent. The hidden constant is, in fact, a universal energy constant, namely the energy of a single oscillation or EM wave. This universal energy constant for light is that same "isolated quantity of energy" de Broglie searched for, i.e., the fundamental small quantum of light’s energy:
This fact is easily verified by solving Planck’s incomplete formula for the energy of a single oscillation of light (see Brooks, 2009a for derivations). The numerical value Planck calculated for his action constant "h" is actually the numerical value of the mean oscillation energy of individual EM waves. The "isolated quantity of energy" hoped for by de Broglie, has been found.
The universal nature of this constant is made clear by consideration of the energy constant over a wide range of wavelengths, time periods and frequencies. The mean energy of a single EM wave remains constant regardless of whether it is a radio wave, microwave, infrared, visible or ultraviolet wave. For low frequency and long wavelength EM waves such as radio waves, the constant mean oscillation energy is spread out diffusely over a large volume of space. At higher frequencies and shorter wavelengths, the energy becomes more concentrated in a smaller volume of space. In the ultraviolet region, the energy of an oscillation becomes extremely dense, being confined to a very small region of space, around 100 nanometers or so in dimension. The amount of energy in a single oscillation is the same, however, regardless of the volume or time period it occupies.
The constancy of the energy of a single EM wave over a variety of wavelengths and time periods means that the elementary quantum of light is constant over a shift in time or space. When a property is constant over a shift in time or space, that property is conserved and represents a universal property. The fundamental relationships are now clear. Just as the electron has a fundamental unit of charge which is conserved and represents a universal constant for electrons, light has a fundamental unit of energy, "h", which is conserved and represents a universal constant for EM waves.