The Fundamental Physics of Electromagnetic Waves Part 3

Virtual thermal effects of resonant EM waves

When resonant EM waves perform work on a system and increase one or more oscillation amplitudes within the system, that increased oscillation energy is free to be transformed into work within the system. In the case of the aqueous solvent system described in the experimental example above, the vibrational oscillations of the solvent water molecules were excited. This in turn led to a change in the behavior of the water as a solvent. The resonant water dissolved 26.0 g/100 ml of NaCl, while the thermal water dissolved only 23.8 g/100 ml. To what temperature would the thermal system need to be raised, in order to dissolve the same amount of NaCl that the resonant system dissolved, all else being equal? This is readily calculated by setting the total element energy in the resonant system equal to the thermal energy, and solving for temperature "T":

In order to dissolve the same amount of NaCl in the thermal system, that the resonant system had dissolved, the thermal system would have had to be heated to 46 ° C. The water in the resonant system behaved as though it had been heated to 46 ° C, even though it had not. The EM waves provided a virtual thermal effect in the resonant solvent system.

Energy efficiency of resonant EM waves

As Helmholtz described many decades ago, energy can be transformed and converted from one form to another, "…heat, electricity, magnetism, light, and chemical affinity ". The efficiencies with which these transformations take place is not uniform across all conversions of energy. Depending on the process and desired end-result or product, the energy transformation efficiency can vary widely. For example, in the water solvent example given above, one would need to heat the water to 46 ° C, in order to dissolve the same amount of salt that the resonant water system had dissolved. Heating 500 ml of water to that higher temperature would require at least 52 kJ of energy.

On the other hand, the light source which provided the resonant vibrational EM waves to the resonant system consumed only 2.1 kJ of energy. (Mortenson & George, 2011). The total additional energy required to achieve the desired end-result or product (i.e., dissolve more salt), is far less with the resonant EM waves: ninety-six percent (96%) less, in fact. The total extra heat of dissolution work performed by the resonant water on the solute was 1.4 kJ. The energy transformation efficiency for the resonant system was 67%. If one were to heat the thermal water to increase its temperature by 25°, using the 52 kJ of energy, the efficiency of the thermal energy conversion into heat of dissolution would be only 3%. There is more than an order of magnitude difference between the energy conversion efficiency of the resonant EM system and the thermal system.

Boltzmann weighting

Under Boltzmann mechanics for purely random and chaotic thermal systems, the elements (e.g., molecules) in a system adhere to a thermal distribution curve (Figure 3.a., below). In general terms, at low temperatures, most of the elements or molecules are at the lowest possible energy level or ground state. As the temperature in the system increases, the elements begin to leave the lower energy levels and populate the upper energy levels. At very high temperatures, several of the upper energy levels may be populated, leaving few molecules in the lowest ground state. The distribution of elements in the energy levels is determined with the Boltzmann factor:

This is a weighting factor that determines the probability that an element will be in the "nth" energy state when the system is in thermodynamic equilibrium. The Boltzmann factor excludes consideration of resonant work energies (which are orderly), and assumes completely random motions in the system. Helmholtz energies are thus typically assumed to be at a minimum when Boltzmann mechanics are applied.

Fig. 3. Comparison of energy level population states under thermal conditions and resonant EM conditions. Upper energy level populations are increased as temperature increases. Absorption of resonant EM waves produces an irregular resonant energy distribution curve. This can result in system behavior equivalent to a "virtual" thermal distribution curve.

When a system is exposed to resonant EM waves, a "virtual" thermal effect can be produced, as in the aqueous solvent example above. In such a case, the "virtual" thermal distribution may be determined using a modification to the Boltzmann weighting factor:

in which the resonance factor, "rf" is included. The resulting thermal distribution curve reveals the energy state distribution curve of the thermodynamic system that would result in the same desired product or behavior that is produced by the system absorbing resonant energy. The assumptions of randomness in the Boltzmann mechanics do not apply to resonant EM systems, with their uniform work energies, and systems exposed to resonant EM waves do not follow the smooth thermal distributions curves, however. Individual energy levels in the system may be selectively populated, changing the shape of the traditional smooth curve, to a bulging or "lumpy" energy distribution curve. (Figure 3b., above). Absorption of resonant EM waves initially results in increased population of an upper energy level. As the energy is converted to work in the system, the energy state devolves and relaxes. When all of the work energy has been spent, a thermal distribution is once again exhibited. Depending on which energy level(s) are selectively populated, the work performed will vary and can include speeding the rate of a reaction in a catalytic manner, e.g., virtual thermal effects can replace chemical activation energies. (Fukushima J. et al, 2010)

Equilibrium constant

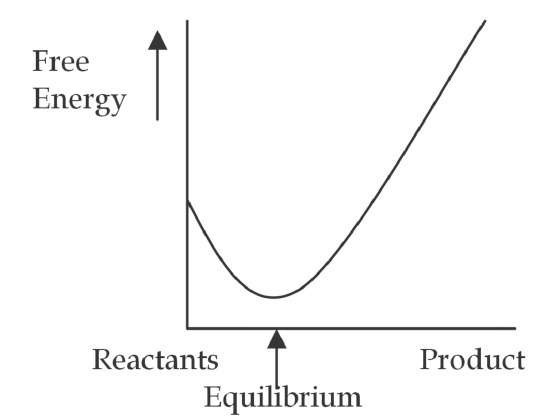
In chemical and materials systems the work performed by the resonant EM waves can also shift the equilibrium of the system and produce dramatic changes in its chemical and material dynamics. In the dynamic equilibrium of chemical and material systems, in which reactants are transformed into products at the same rate products are transformed back into reactants, the equilibrium constant "K" indicates the point of dynamic equilibrium (product-to-reactant concentration ratio). Systems with a large equilibrium constant contain mostly product, while a low "K" indicates mainly reactants.

Fig. 4. a. Thermal system

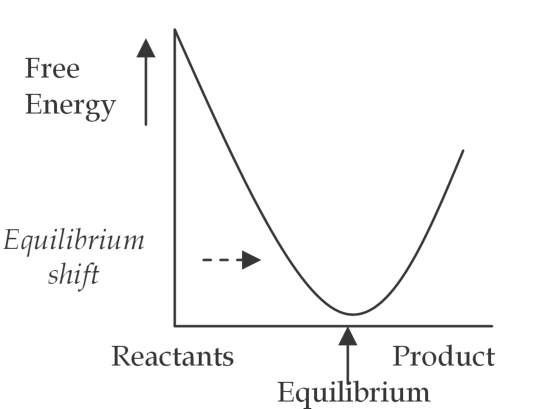
Fig. 4. b. Resonant system

In statistical thermodynamics the equilibrium constant is proportional to another natural log, K « e-AE/RT" (where AE is chemical free energy). When resonant EM waves are present in a system, the resonance factor properly appears in the denominator of the power notation, i.e., "rfRT" to reflect the total increase in system energy. If the resonant EM waves increase chemical free energy, "AE", the ratio of chemical free energy to system energy remains the same. The equilibrium constant does not change, however the EM waves act as a catalyst and increase the rate of the reaction. (If the chemical free energy decreases, i.e., the resonance factor is less than "one", the EM waves will act as a negative catalyst and slow the rate of reaction.) When resonant EM waves are absorbed and transformed to something other than chemical free energy, then AE/rfRT < AE/RT , and the equilibrium constant will increase. Resonant EM waves that perform useful work on a system can thus increase the equilibrium constant, "K", and increase the actual concentration of desired products. Resonant EM waves can cause a shift of the equilibrium curve. (Figure 4.b., above) In other words, resonant EM waves can achieve results not obtainable with classical catalysis or thermodynamics. (Brooks and Abel, 2007, Blum et al, 2003, Fukushima H., 2010, and Roy et al, 2002)

Conclusion

The two fundamental formulae which formed the foundations of quantum mechanics and 20th century physics were both incomplete in regard to electromagnetic waves. The quantum formula was missing a time variable and energy constant, due to a minor inadvertence in Max Planck’s derivation of the blackbody equation. Unforeseen consequences occurred as a result. The identity of the true elementary particle of light – the single EM oscillation – was obscured. Mathematical nomenclature for frequency became incomplete. Calculations of the mass, momentum, and force of EM waves were made impossible. Paradoxical principles including the classical limit, the uncertainty principle, and the complementarity principle were made necessary. Dimensionality of the fine structure constant was hidden, and great confusion arose over the wave vs. particle nature of light. Use of the complete quantum formula remedies these difficulties and provides a sound foundation for a certain and realistic quantum mechanics.

Likewise, the thermodynamic formula derived in Planck’s blackbody work was not an inclusive or complete formula for energy dynamics. The complete energy dynamics formulae allow the resonant EM work energies in systems to be accounted for mathematically, both at the macroscale and microscale. Traditional Boltzmann mechanics cannot be strictly applied to EM waves, because Boltzmann mechanics assume completely random motions. Absorption of uniform EM waves requires modifications of Boltzmann weighting. Resonant EM waves can provide virtual thermal effects, decreased energy requirements, and increased energy efficiencies. Depending on how their energy is converted to work, resonant EM waves can act as catalysts – changing chemical or materials reaction rates – or they can shift reaction equilibria altogether, producing effects and products not seen or obtainable under typical thermodynamic conditions. A new and powerful scientific paradigm is being revealed in the fundamental physics of electromagnetic waves.