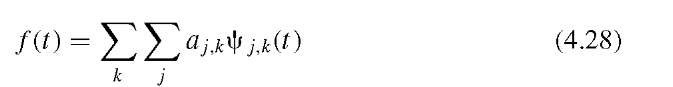Comparison of Frequency-Domain Analysis To Wavelet Analysis (Biomedical Image Analysis)

Both the Fourier transform and the wavelet transform provide linear decompositions of a signal f (t) into coefficients ak such that

andare the basis functions. In the case of the Fourier transform, theare complex oscillationsThese oscillations are continuous from which implies that the function f (t) is aperiodic signal that stretches fromThe wavelet transform, on the other hand, uses basis functions with compact support. Furthermore, the wavelet transform relies on a two-dimensional set of coefficientsso that

and the set of basis functionsreflects the scaled and shifted mother wavelet. As a consequence of the compact support of the wavelets, f (t) itself may be nonperiodic or have compact support itself. The assumption of a periodic f(t) is often violated in the discrete Fourier transform and leads to techniques such as multiplication with a window function to eliminate the discontinuity between the start and the end of a discretely sampled signal or image. These considerations do not apply to the wavelet transform.

The most crucial difference between the Fourier transform and the wavelet transform is the latter’s ability to retain spatial information. A Fourier-transformed image contains the summed-up contributions of all image areas toward a spatial frequency irrespective of their location. A wavelet-transformed image, on the other hand, separates the image by frequency bands while it retains the spatial information in each band. For this reason, nonlinear and adaptive filter techniques can be designed that would not be possible with the Fourier transform. Examples of nonlinear techniques are the filter functions shown in Figures 4.10 and 4.15. Examples of adaptive filters include a locally variable threshold in Figure 4.10, determined from the local noise variance. Furthermore, wavelet-based filters can include a priori spatial knowledge: for example, a restriction to segmented areas of the image.

A second fundamental difference between the Fourier transform and the wavelet transform is the ability of the wavelet transform to control the level of detail with the scaling variable, s in Equation (4.4). The Fourier transform, in comparison (see Figure 4.18), merely provides the global contribution of the frequency components toward the signal. The Fourier transform can be restricted in time, leading to the windowed Fourier transform, but as the window size decreases, less information about high frequencies will be provided. Whereas the Fourier transform is restricted to periodic sinusoidal oscillations, the wavelet transform allows the flexibility of choice of a suitable wavelet basis function for optimized smoothness and frequency response of the filter bank.

Another important property of the wavelet transform cannot readily be quantified. The application of filters to multiple scales retains self-similar properties. Many objects have some self-similar properties that are perceived as natural. Therefore, the results of wavelet-based filters often appear more natural than those of Fourier-or convolution-based filters. The most prominent example is wavelet-based image compression. Lossy image compression implies that the original image cannot be reconstructed—a price to be paid for very high compression rates. A very common method of lossy compression is based on the discrete cosine transform (Section 3.3), whereby small square areas of the image are transformed and high-frequency coefficients are discarded. This compression method leads to typical block artifacts. Wavelet-based compression does not show these artifacts, and the perceived image quality of images highly compressed with a wavelet algorithm is much higher than that of images compressed with the discrete cosine transform. The advantages of wavelet-based compression are so high that this new compression method became part of the JPEG-2000 standard. Wavelet-based image compression is covered in detail in Section 12.3. The key differences between the Fourier transform and the wavelet transform, with its implication on filters, are summarized in Table 4.2.

FIGURE 4.18 Comparison of the Fourier transform to the wavelet transform. The Fourier transform of a signal (A) provides the global frequency components without respect to their location in time. A windowed Fourier transform (B) allows some localization with respect to time, but as the windows become smaller in time, so does their ability to provide high-frequency information. The wavelet transform (C), by merit of the scalability of the basis functions, provides localized high-frequency information.

TABLE 4.2 Comparison of the Wavelet Transform to the Fourier Transform