Abstract
The analysis of partially-observable discrete stochastic systems reconstructs the unobserved behavior of real-world systems. An example for such a system is a production facility where indistinguishable items are produced by two machines in stochastically distributed time intervals and are then tested by a single quality tester. Here, the source of each defective item can be reconstructed later based solely on the time-stamped test protocol.
While existing algorithms can reconstruct various characteristics of the unobserved behavior, a fully specified discrete stochastic model needs to exist. So far, model parameters themselves cannot be reconstructed.
In this paper, we present two new approaches that enable the reconstruction of some unknown parameter values in the model specification, namely constant probabilities. Both approaches are shown to work correctly and with acceptable computational effort. They are a first step towards general model parameter inference for partially-observable discrete stochastic systems.
Keywords: partially-observable discrete stochastic system, Hidden non-Markovian Model, incomplete model, parameter inference.
Introduction
Many real-world systems can be regarded as partially-observable discrete stochastic (PODS) systems: their stochastic internal behavior can be modeled as a discrete stochastic model such as a non-Markovian stochastic Petri net [1,3]. And this internal behavior is of interest, but not directly observable; it can only be inferred through externally observable signals that are linked to the internal processes.
Analysis of these systems is the process of inferring the unobserved behavior of the real system using a time-stamped protocol of its signal emissions and the discrete stochastic model. It allows for additional insights into the inner workings of the real system.
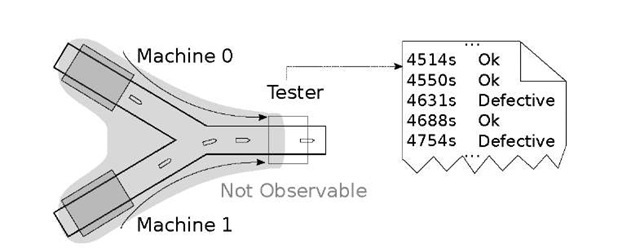
A simple example of such a system is a small section of a production facility with two machines that produce indistinguishable items, and a quality tester to test items coming from both machines (see Figure 1). At the quality tester, the source of each item is no longer determinable (and thus unobserved), but the test protocol containing the time-stamped individual test results is a trace of the corresponding externally observable signals. Here, reconstructing the source of defective items can be of interest for purposes of quality assurance.
Fig. 1. Schematic representation of the partially-observable Tester system
So far, existing analysis algorithms only attempt to reconstruct the specific system behavior in time intervals for which signal protocols exist [7,11]. The model specification itself, which describes all possible behaviors has to exist beforehand. For the "Tester" system in Figure 1, one would like to determine the individual probabilities of the two machines to produce defective items, but these parameters are part of the model specification and therefore cannot be reconstructed using the existing approaches. This severely limits the applicability of the analysis of PODS systems, since it assumes that the unobservable system must have been be completely observable after all at some point in time, in order to derive the specification.
In this paper, we present two approaches that enable the reconstruction of some parameters of the model specification: We reconstruct the most likely values for unknown constant probabilities in incomplete model specifications with the help of a signal protocol. The first approach is an iterative algorithm that relies on an arbitrary initial estimate for unknown parameter values and itera-tively improves that estimate. The second approach is based on computationally expensive symbolic computations in order to determine the most likely values directly.
The remaining paper is structured as follows: Section 2 classifies this work with respect to existing contributions. Section 3 introduces the current state-of-the-art in the analysis of PODS systems. Sections 4 and 5 describe the two new approaches. These are then evaluated in Section 6. The paper is concluded in Section 7.
Related Work
To our knowledge, the inference of model parameters for discrete stochastic systems from time-stamped stochastic signal emissions that represent partial observations of the real system has not been attempted before. However, similar problems have been solved before successfully.
Deriving the parameters of a linear dynamical system description from time series is a widely used tool in econometrics [2]. Here, a time series consists of vectors of continuous-valued quantities sampled at discrete time intervals, where each sample describes the complete system state. More recent advances in that area were made by Malyarenko et al. [14]. These analyses assume, however, that the observations are not the result of a completely stochastic process. Rather, they are assumed to be based on a combination of deterministic processes and interference from noise. The parameters to be determined are thus the coefficients for the influence of each component. Our focus on the other hand, is to derive parameters of a truly stochastic system with a discrete number of system states. Additionally, our samples are consequences of internal system state changes, which may occur at any real-valued point in time.
The inference of model parameters for truly stochastic discrete processes has been performed by many researchers: Hidden Markov Models are routinely used in speech recognition and other fields to learn all parameters of a hidden model from observed data alone [15]. However, in HMMs, all model parameters are constant probabilities and the models are discrete in time, limiting the expressiveness of the models. Thus, HMMs are not directly applicable to most real systems.
For some application fields, specialized analysis algorithms have been developed: Gibson et al. derived parameter values of a compartmental epidemiological model from partial observations of the number of specimens in some of the compartments [9]. Boys et al. [5] and Wang et al. [16] applied different algorithms to the problem of finding the rates at which chemical and biochemical reactions occur in stochastic settings where the number of chemical reactants is so low that the effects of randomness become important. In both cases, the observed data consisted of time series of the number of molecules for each type of reactant.
All of these approaches, however, impose the same two limitations: the stochastic model itself has to be Markovian, restricting the classes of discrete stochastic systems that can be modeled and analyzed. And the observations from the real system are sampled at discrete points in time. Thus, the approaches are only applicable to systems where (partial) observations of the system state can be made regularly "on demand" at regular intervals.
We, on the other hand, focus on discrete stochastic systems whose state changes can follow arbitrary probability distributions. And our approach relies only on "incidental" observations of signals that the real system emits on some of its state changes. Thus, our approach works even if the observations are made irregularly and if they are only stochastically linked to the system state changes (i.e. a signal can have multiple possible causes, and a state change can cause one of many different signals to be emitted). Consequently, our approach is computationally more expensive and thus cannot analyze models as big as the other approaches.
Background
In this section, we present background information relevant to the understanding of the new algorithms. We introduce Hidden non-Markovian Models (HnMMs) as a way of modelling PODS systems, and the Event-Driven Proxel algorithm as a means to analyze these models.
PODS Models
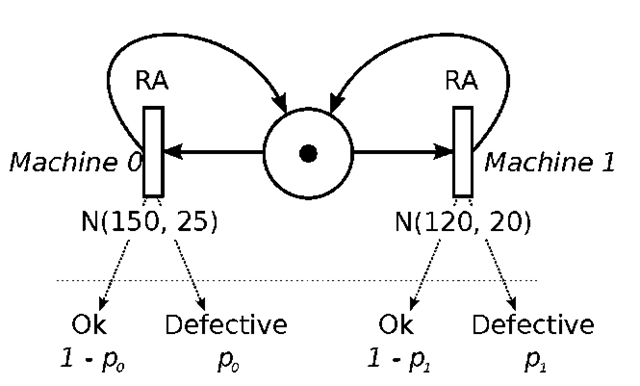
Hidden non-Markovian Models (HnMMs) were introduced as a paradigm to model arbitrary PODS systems [12]. They can be represented compactly by extending non-Markovian stochastic Petri nets [1,3]: In non-Markovian SPNs, the system is modeled through places (hollow circles) that contain a number of markings (small black circles), whose distribution represent the current system state. The system state can only change through the firing of transitions (hollow rectangles), which destroy markings in places leading to the transition through arcs (arrows) and create markings in places lead to by the transition. To represent HnMMs, this specification is extended by adding probabilities for the transitions to emit certain externally-observable symbols when they fire.
The representation of the Tester system from Figure 1 as an HnMM is given in Figure 2: The system has only a single state, so the only place always contains a single token. The two machines produce items in N(150, 25) and N(120, 20) distributed time intervals, respectively. Every production of an item emits a symbol "Ok" or "Defective" (as determined by the system’s quality tester). Machine 0 produces defectives with probability p0, Machine 1 with pi. In our application scenario, these two probabilities are unknown and thus the model specification is incomplete.
This model is slightly simplified since item production is the only possible event and each production event yields the item’s test predicate right away. This simplification in the model can be made when the time span between item production and testing is approximately constant. Then, each time of production can trivially be derived from the time of testing (by subtracting that constant time span from the test time stamps) and be recorded in the trace along with test results.
If those symbol emission probabilities were known, existing analysis algorithms could reconstruct the unobserved behavior for a system specified in this manner. The most efficient known algorithm for this task is detailed in the next section.
Analyzing PODS Systems
Several algorithms exist for the analysis of different classes of PODS systems. In this paper, we will only detail the analysis algorithm for the class Eau [12], to which the Tester model belongs. The algorithmic modifications presented in this paper to derive parts of the system specification can, however, be applied to all other classes of PODS systems and their analysis algorithms as well.
Fig. 2. The Tester system modeled as a Hidden non-Markovian Model
For models of class Eaii, all internal state changes result in an externally observable symbol emission. In the HnMM representation, this means that all transitions emit symbols in all cases. Yet, since the type of the symbol is allowed to vary stochastically, and multiple transitions are allowed to emit the same symbol, the system state cannot be inferred unambiguously from the emitted symbol.
The consequence of this limitation is that all points in time where the system changes its state are known to the outside observer. Hence, it is certain that no event occurred between the emission of two symbols. This restriction allows Eall models to be analyzed using the efficient event-driven analysis algorithm described in the next section.
The Event-Driven Analysis Algorithm. The event-driven analysis algorithm for HnMMs [6] is derived from the state space-based Proxel simulation method [10,13]. It is a simplified version of the former algorithm, based on the observation that for Eall models no events occur in between two symbol emissions and thus possible system behaviors need only be studied at the times of symbol emissions.
The algorithm therefore divides the time domain into time steps corresponding to the time between two signal emissions. For each time step, it follows all possible single system state changes (i.e. those that can occur exactly at the end of the time step and are consistent with the trace) in parallel and computes the likelihood for each of them. The analysis result is then the set of all states that the system can be in after it has emitted the last signal recorded in the trace, along with the probability of being in each state.
In effect, the algorithm dynamically builds and solves the underlying inhomo-geneous Markov chain for each time step, where the set of Markov chain states is the combination of the set of reachable system states from the HnMM with supplementary variables that store the age of non-Markovian transitions in each state.
For a given point in time, the possible system evolutions are stored as so-called Proxels, tuples of type (m,T,p). Here, m is the marking of the system state in the HnMM’s underlying Petri net. The vector t contains the supplementary variables, the ages of all relevant transitions (i.e. the duration for which each of these transitions is already active); p is a measure of probability for the marking-age combination.
The analysis starts by creating Proxels for the known initial system state (or states) at t = 0. Then, successor Proxels are created iteratively for each time step, one for each possible single state transition of each Proxel. Thus, these new Proxels represent all states that are reachable from Proxels of the previous emission time. The probability of a Proxel representing a state change through transition i is hereby computed as the product of:
— the probability of the predecessor Proxel.
— the probability that no event happened in between the two symbol emissions. This is computed by numerically solving an ordinary differential equation based on the hazard rate of all active transitions over the time interval between both symbol emissions [10].
— the hazard rate ^(t+At) of transition i, which is the likelihood of transition i to fire in exactly than instant. Here, At is the time between the previous and current symbol emissions.
— the probability that the transition in question emits the observed symbol, as recorded in the HnMM specification.
The algorithm so far would result in an exponential growth in the number of Proxels over time, since each Proxel of a given time step causes the creation of multiple Proxels (one for each possible state transition) at the next time step. This effect is countered by Proxel-merging: If two Proxels with identical marking and age vector (m,T,p\) and (m,T,p2) exist for the same time step, they are merged to form a single Proxel (m,T,p\ + p2). Proxel merging mitigates the exponential growth of the number of Proxels and for most models even creates an upper bound for the number of Proxels per time step.
The algorithm in pseudocode is detailed in Algorithm 1.
Encoding Additional Information. The algorithm as detailed above computes the probability measures for all reachable states, but does not retain any information on the history of how a state was reached. Thus, the set of Proxels output by the algorithm only contains information on which states the system could be in after emitting the last element of the protocol, and with what probability.
In order to be able to reconstruct other characteristics of the unobserved behavior, the Proxel definition needs to be extended with further supplementary variables that store information on those characteristics. This can for example be the number of past occurrences of a particular event. In the case of the Tester model, one would encode the number of times that machine 0 has produced defective items so far. This way, the set of Proxels at the final time step contains detailed information about how often the relevant event may have occurred with what probability. This information can then be used to compute a likelihood histogram, the expected value or the most likely value for the quantity in question.
Algorithm 1. Pseudocode for the event-driven Proxel solver.
The downside of this approach is that the number of reachable Proxel markings increases by a constant factor depending on the range of the new supplementary variable. Thus, computation time and memory consumption increase by at least the same factor. While this often has a heavy impact (the computation time for the Tester model increases about 50-fold), it does not in principle affect the feasibility of the analysis.
With this modification, the algorithm is able to reconstruct the likely system behavior during the time interval for which the trace was recorded. However, for reasons detailed in the next section, it does not allow for the reconstruction of model parameter values.
Obstacles for the Reconstruction of Model Parameters. By encoding additional information using supplementary variables, one could theoretically also reconstruct parts of the system specification. In the example of the Tester model, the unknown defect probability of each machine is simply the number of produced defective items divided by the total number of produced items. The latter can be estimated from the expected value of the probability distributions associated with the production process. And the former could be derived from a model analysis for which the number of produced defective items from one of the machines is encoded into each Proxel as a supplementary variable1.
However, the parameters that are to be computed by this algorithm are also required as inputs to it: The unknown defect probabilities are the symbol emission probabilities of the model. Thus, the algorithm could only be used to confirm a known set of parameters, but not to compute them in the first place. The main contribution of this work are therefore two new algorithms that resolve this contradiction. These are detailed in the following sections.
Iterative Analysis Algorithm
The iterative analysis approach was developed based on conclusions drawn from the nai’ve approach of simply guessing the unknown values and assuming that the guess will not impact the accuracy of the analysis. This naive approach was evaluated using the Tester system, where the symbol emission probabilities of both machines to produce defective or working items are unknown. For the Tester, the "real" system is actually a simulation model. Therefore, the usually unob-servable quantities can be observed here, and the quality of the reconstructed parameter values can be assessed through comparison with the actual system parameter values.
Without additional information, a suitable guess for the defect rates of the two machines is that both are equal and together account for all defects actually occurred, i.e. p0 = p1 = 0.07. Using these estimates, the reconstructed defect probabilities are 0.081 and 0.060, respectively, while the actual defect probabilities are 0.100 and 0.046. The data shows that the initial assumption was wrong and that there is a big discrepancy between the reconstructed parameter values and the actual ones. However, it also shows that in this case the result of the reconstruction is closer to the (usually unknown) actual system behavior than the initial guess.
This observation that an event-driven analysis "refines" estimates of unknown parameter values lead to the following iterative analysis algorithm: initially, one guesses arbitrary initial values for the unknown parameters. Then, the most recently estimated set of parameter values is iteratively used to perform an event-driven Proxel analysis in order to obtain more accurate estimates for the parameters. The iteration process terminates, if the difference in the parameter values between two iterations falls below a given threshold. This is shown in Algorithm 2.
Algorithm 2. Iterative Algorithm for Parameter Reconstruction
Figure 3 shows the analysis result for the defect probability of Machine 0 of the first 14 iterations for the Tester model. With every new iteration, the results further approach the actual system behavior. And the results converge quickly to a value close to the actual system behavior. The difference between the value of convergence and the actual system behavior is tested and discussed further in the "Experiments" and "Conclusion" sections.
Fig. 3. Computed expected defect probability of Machine 0 using iterative analysis. Iteration 0 is the initial estimate. The dotted line represents the actual system behavior.
The size of the difference between the reconstructed parameter value of two iteration steps (and thus the rate of convergence) seems to correspond to the slope of the likelihood polynomial for that parameter (cf. figures 3 and 4). We therefore assume that this algorithm explores the parameter space in the same way that the gradient descent algorithm does. In this case, it will reliably find a parameter set that is a local likelihood maximum. It may, however, not necessarily find the global likelihood maximum (i.e. the most likely parameter set). All experiments conducted support this hypothesis, but no formal proof of this behavior exists as of yet.