Departure Process in Finite-Buffer Queue with Batch Arrivals (Queueing Theory) (Analytical and Stochastic Modeling) Part 2

Numerical Results

In this section we present sample numerical results for conditional mean of departures before fixed t i.e. for the expression Enh(t), where the symbol En stands for the mean on condition £(0) = n. In computations we use firstly the following obvious identity:

and next the algorithm of approximate numerical Laplace transform inversion introduced in [1]. The base of the algorithm is the Bromwich inversion integral that finds value of the function g at fixed t > 0 from its transform g as

whereis located on the right to all singularities of g. Using trapezoidal method with step h to estimate the integral in (47) we obtain the approximation gh(t) of g(t) in the form

 

Setting series representation:

 

where

and

Let us take into consideration the following Euler formula for approximate summation of alternating series:

where parameter m is usually of order of dozen and parameter n – of order of several dozen ([3]). Applying (53) in (48) we finally obtain

where typical values of parameters are following (see [l]): m = 38,n = ll,A = l9, L = l.

A precise evaluation of the estimation error in (54) is not possible, first of all, due to the lack of such an estimation for the Euler summation formula (53). The practice has shown that a good evaluation of the error one can get by executing the calculation twice, and changing by l one of the parameters. Then the difference between the results, e.g. for A = l9 and A = 20 provides a good evaluation of the error estimation. More details can be found in [l] and [3].

Let us consider the system of size N = 4 in that individual service times have Erlang distributions with parameters n = 2 (shape) and ^ = l (rate) i.e.

thus the mean service time is 2. Let us take into consideration two different simple batch size distributions: p2 = l (each arriving batch consists of 2 packets) and pi = p2 = The system with the second possibility we denote by M1,2/G/l/N. Below we present a numerical comparison of values E0h(t) and ENh(t), computed for t = 20, 50, l00, 200, 500 and l000 for these two systems. Possibilities of underloaded (p < l) and overloaded system (p > l) are presented separately. Each time values of the arrival rate parameter A are selected in such a way to fix the same value of p for both systems.

In the table below (Table l) we present results obtained for A1 = 0.l5 (for M2/G/l/N queue) and A12 = 0.20 (for M1’2/G/l/N queue) that gives q = 0.6 < l in both systems.

Table 1. Conditional means of departures before t for p = 0.6 (underloaded systems)

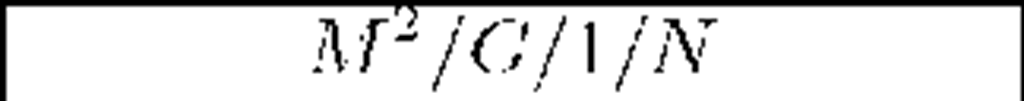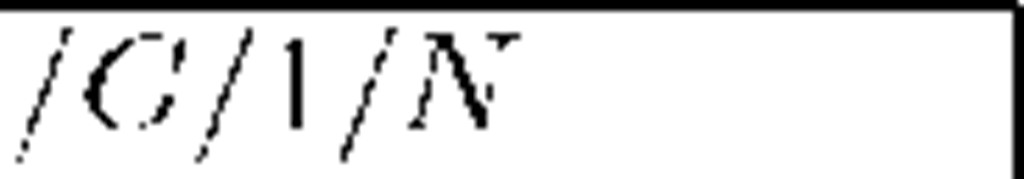t
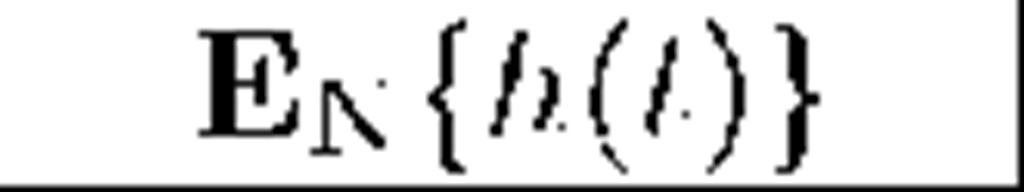20	4.299	7.133	4.479	7.334
50	12.204	15.059	12.632	15.523
100	25.384	28.240	26.231	29.121
200	51.745	54.600	53.427	56.318
500	130.827	133.682	135.016	137.907
1000	262.630	265.486	270.998	273.889

Table 2. Conditional means of departures before t for p = 2.4 (overloaded systems)

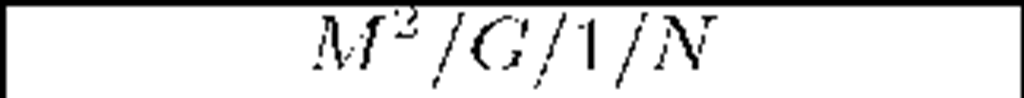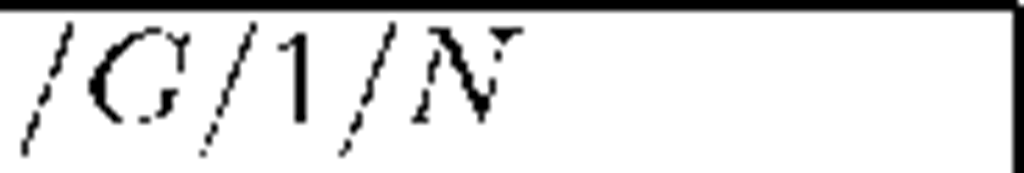t
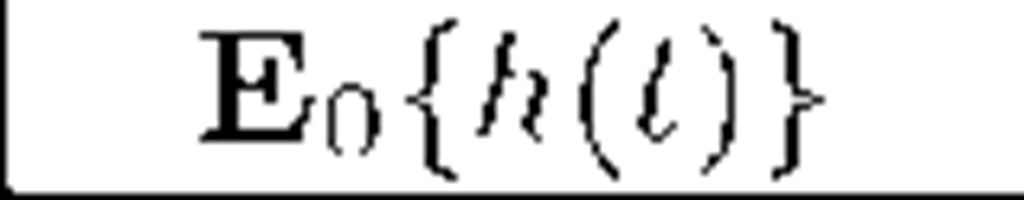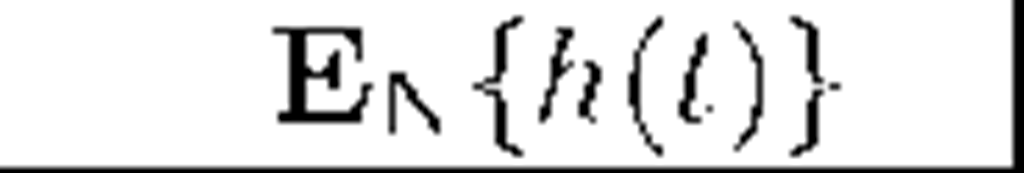20	8.559	9.495	8.798	9.601
50	22.997	23.933	23.470	24.273
100	47.061	47.996	47.922	48.726
200	95.187	96.123	96.828	97.631
500	239.568	240.503	243.545	244.348
1000	480.202	481.138	488.073	488.876

The next table present similar results for Ai = 0.6 and A1,2 = 0.8 (so for p = 2.4 > 1 in both systems).

Considering the above results one can observe that the average number of departures is greater for the M1,2/G/1/N system (for the same p). But the difference is the smaller, the greater is traffic load p. Similarly, of course, the mean of h(t) is greater in the case of the opening with maximum number of customers present than in the case of the system empty at t = 0. The difference decreases as t increases.