Special Purpose Elements (Finite Element Method) Part 2

Coupling of FEM and BEM

Another effective method of dealing with infinite domains is to use the FEM coupled with the Boundary Element Method (BEM). The FEM is used in the interior portions of the problem domain where the problem is very complex (nonlinear, inhomogeneous, etc.), and the BEM is used for the exterior portion that can extend to infinity. Much research work has been done in this area.

Coupling of FEM and SEM

Coupling of the FEM with the Strip Element Method (SEM; see Section 10.5) can also effectively handle infinite domains. In such a combination, the FEM is used in the interior portions of the problem domain where the problem is very complex (anisotropy, nonlinear, inhomogeneous, complex geometry, etc.), and the SEM is used for the exterior portion that can extend to infinity. This combination is applicable for domains of anisotropic materials.

Finite Strip Elements

Using finite strip elements instead of the conventional finite elements can be a very effective method for solving structural problems involving regular geometry and simple boundary conditions. This method was developed by Y. K. Cheung in 1968. In his method, the structure is divided into 2D strip or 3D prism or layer sub-domains. This method usually requires the geometry of the structure to be constant along one or two coordinate axes so that the width of the strip or the cross-section of the prism or layer will not change from one end to the other.

Figure 10.9. Finite strip elements used in a plate.

Consider the plate modelled with finite strip elements shown in Figure 10.9. It is assumed that the strips are connected to each other along a discrete number of nodal lines that coincide with the longitudinal boundaries of the strip. The finite strip method can be considered as a special form of the finite element procedure using the displacement approach. The standard finite element approach normally uses polynomial shape functions in all directions, but the finite strip method only uses simple polynomials in some directions, and continuously differentiable smooth series in the other directions. The general form of the displacement function for the finite strip method is thus given as a product of polynomials and series. Hence, for each strip shown in Figure 10.9, the displacement function is given as

where fm(x) is the polynomial shape function and Ym is the continuous series that is able to satisfy the boundary conditions at the structure boundary.

The choice of fm (x) and Ym in Eq. (10.31) is very important, as it affects the convergence to the correct results. As a rule, the series part, Ym, should satisfy the end conditions of the strip. For example, for a simply supported plate strip in bending, the displacement function should be able to satisfy the conditions of both deflection, w, and curvature, d2w/dx2, being equal to zero at the two ends. The polynomial part, on the other hand, must also be able to represent a state of constant strain in the x direction, to ensure that the strain will converge towards the true strain distribution as the mesh is further refined. As a whole, the displacement function or shape function must also satisfy the compatibility of displacements along boundaries with neighbouring strips.

As an example, let us consider the plate shown in Figure 10.9 to be simply supported at both ends in the y direction. To satisfy the conditions at the ends would mean satisfying Y(0) = 0, Y”(0) = 0,Y(a) = 0 and Y”(a) = 0, where a is the length of the strip. A suitable series function would thus be

 

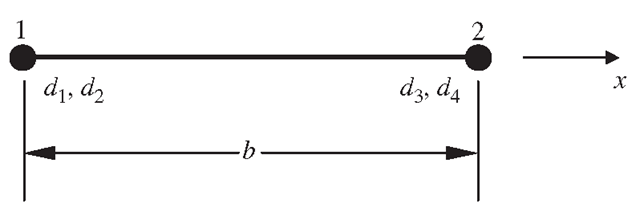
Figure 10.10. A strip element cross-section with two nodes.

As in the finite element method, the choice of shape functions depends upon the number of nodes in the x -direction for each strip element, and also on the nodal degrees of freedom. For example, in the case of a straight line with two nodes, as shown in Figure 10.10, and if the displacements and their first derivatives are the nodal parameters, then the polynomial part of the displacement function can be given as

where di to d4 are the nodal parameters, and the functions Ci are given as

Therefore, if Eq. (10.33) is substituted back into Eq. (10.31), the displacement function can be written as

or

where

are the shape functions for the stated example above. The shape functions would therefore vary from problem to problem with different choices of both the polynomial part and the continuous series part. Once the shape function has been formulated, the remaining procedure is actually similar to that of using the finite element method. Based on the constitutive equations and the variational principles discussed when formulating the finite element equations, the corresponding stiffness matrices and load vectors can be similarly obtained. This is then followed by assembly of these matrices for different finite strip elements to form the global matrices. Finally, the matrix equation can then be solved using standard matrix solution techniques. The size of the matrices obtained is usually smaller as compared to that using the conventional finite element method, and this makes the solving of the equations a relatively easier task. The above procedures are applied to a 2D plate modelled with strip elements. A similar approach can also be used when formulating the shape functions, and hence the element matrices for 3D prisms or layers.

Strip Element Method (SEM)

The SEM is a semianalytic method for stress analysis of solids and structures. It has been mainly applied for solving wave propagating in composite laminates. The SEM is a semi-exact method that discretizes the problem domain in one or two directions. Polynomial shape functions are then used in these directions, together with the weak forms of the system equation, to produce a set of dimension-reduced special differential equations. These differential equations are then solved analytically.Due to the semianalytic nature of the SEM, it is applicable for problems of arbitrary boundary conditions, including the infinite boundary conditions.

In such a combination, the FEM is used for small domains of complex geometry, and the SEM is used for bulky domains of regular geometry.