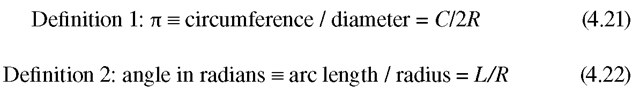Circular logic defines a curve as a line that is not straight and a straight line as one that is not curved. Separating circular geometry from circular logic, a circle is a curve that has completed one cycle, or, said differently, a curve is a portion of a circle. There are two fundamental definitions that relate a circle to the value of pi (π) and to the measure of an angle.
Definitions
Using the two definitions, it is quickly established that there are 2π radians in a complete circle (360°) and that any arc length is the product of the radius times the subtended angle in radians. One of the simplest, most powerful equations available to the spatial data user is
where
|
Degree of Curve |
Highway Definition |
Railroad Definition |
|
1° |
5,729.578’ |
5,729.651’ |
|
2° |
2,864.789’ |
2,864.934’ |
|
5° |
1,145.915’ |
1,146.279’ |
|
10° |
572.958’ |
573.686’ |
|
20° |
286.479’ |
287.939’ |
|
30° |
190.986’ |
193.185’ |
|
45° |
127.324’ |
130.656’ |
|
90° |
63.662’ |
70.711’ |
Elements and Equations
The degree-of-curve definitions are not compatible with the metric system (SI). For that and other reasons, modern practice tends to use the radius and another element to define a circular curve. As shown in Figure 4.7, there are five primary circular curve elements routinely encountered when working with spatial data involving circular curves. Of the ten possible combinations of five elements taken two at a time, the combinations of tangent/length and tangent/long chord are rarely used because of their weak geometry and computational complexity (see, for example, Thompson 1974). Given any other pair of primary circular curve elements, the solution can be found using some combination of equations 4.26 to 4.31.
FIGURE 4.7 Elements of a Circular Curve
Secondary curve elements also labeled in Figure 4.7 include the following:
With reference to Figure 4.7, note the following:
• The word “tangent” is used twice. The straight centerline segment between P/’s is called a tangent. And, one of the curve elements, the distance from the PC to the P/, is called the tangent (of the curve). Added to those two uses, the word “tangent” is also associated with the use of a trigonometric function. The context of usage generally dictates which meaning is intended.
• The radius of the curve meets the centerline (both tangents) at a right angle.
• The angle of intersection is the same as the central angle of the curve.
• The deflection angle is half the central angle.
• The diagram is symmetric. The distance PC to PI equals the distance PI to PT, and a radial line to the PI is perpendicular to the long chord. This right angle statement should not be accepted at face value, but each reader should prove it to him or herself.
Using L = RO, the definitions of trigonometric ratios, the labels assigned to the curve elements, and the diagram in Figure 4.7, it is possible to write the following relationships (^ means “implies that”):
Stationing
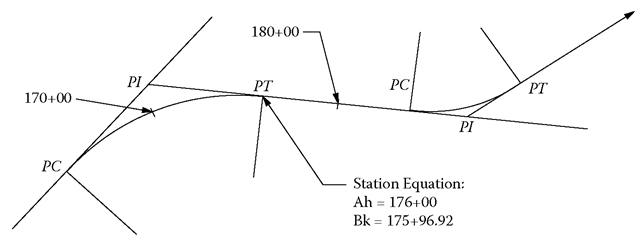
When designing and building a road (or other centerline-referenced project), horizontal distance along the centerline is the basis of stationing. An arbitrary value such as 0+00 or 100+00 is assigned to a point near the beginning of a project, and points on the centerline are stationed as xx+xx.xx (the value of xx+xx.xx being the accumulated centerline distance to the point). Difference in stationing is the horizontal distance along the centerline between stationing values—even along curved portions of the centerline. For example, the distance from station 132+16.58 to station 163+45.32 is 3,128.74 feet. Discontinuities in stationing (either gaps or overlaps) are handled with a station equation assigned to some centerline point. A common format for a station equation is “XXX+XX.XX Back = YYY+YY.YY Ahead.”
Station equation policies vary from one organization to another, but if changes are made to the centerline alignment or if curves are added after centerline stationing is assigned, stationing for the entire project might be reassigned. Since restation-ing is often not practical, a station equation is used to account for gaps and overlaps. In the case of adding a curve, a station equation is used at the end of the curve (PT). The “ahead” station is found by adding the curve tangent distance to the PI station, and the “back” station for the same point is found by adding the curve length to the PC station. Used in reverse, distance along centerline is the difference in station-ing—except when a station equation is encountered. Then, distance along centerline is computed separately on two sides of the station equation. For example, a station equation (175+48.92 BK = 175+50 AH) is used at the end of the curve shown in Figure 4.8. What is the centerline distance between station 170+00 on the curve and station 180+00 on the tangent?
Of course, other changes to the centerline alignment also require a station equation to accommodate the change in length along the revised route. Some changes will lengthen the centerline, causing an overlap at the station equation. Other changes will shorten the centerline and cause a gap between the “back” and “ahead” stations at a point.
FIGURE 4.8 Station Equation Example
Metric Considerations
Stationing is used to identify cross-section locations on road or similar projects. Cross-section spacing of each station or half-station is common. There appears to be no set standard when using stationing on metric-based projects. Some use a 100 meter station with cross-section intervals of 20 or 30 meters. Others use 1,000 meters (1 kilometer) as the station with cross-section intervals every 100 meters. Therefore, each user is encouraged to confirm and/or be specific about stationing policies on any metric project. Possible sources of information include any state department of transportation (DOT) office or the American Association of State Highway Transportation Officials (AASHTO).
Area Formed by Curves
The area of a rectangular-shaped figure is length times width. The area of a circle is developed using small rectangles and tools of calculus. As shown in Figure 4.9, a differential element of area is the length (circumference at that radius distance from the center) times an infinitesimally small width (dR). Written in calculus as a summation of an infinite number of small rings, the area of a circle with radius R is computed as
A sector of a curve is defined as the “pie-shaped portion” of a circle, and the segment of a curve is defined as that area between the arc and chord of the curve. Both are shown in Figure 4.10. Area of a curve sector is linearly proportional to the total curve area in the same manner as a central angle is proportional to a complete circle. If the central angle is 1/4 of 360°, then the area of the sector is 1/4 the area of the circle; or if the central angle is 0.4475 of 360°, then the area of the sector is 0.4475 π R2. For any sector, the area of the sector is
FIGURE 4.9 Area of a Circle
where Δ = central angle in decimal degrees.
FIGURE 4.10 Area of a Sector and Area of a Segment
The area of a segment is computed as the remainder left when the area of the inscribed triangle is subtracted from the area of the corresponding sector, as shown in Figure 4.10. The area of a triangle is 1/2 base times height. Using the radius as the base and the radius times sin of central angle as the height of the inscribed triangle, the segment area is computed as
And, with a bit of algebraic manipulation,
Note that the last expression in equation 4.36 is really Δ in radians minus the sin of Δ.
Area of Unit Circle
What is the area of a unit circle (R = 1)? The answer is π. If the area of a unit circle is computed as the sum of a large number of small triangles, the answer will be in error by the accumulated segment area between the arc and the chord. As a larger number of triangles is used, the error becomes very small. As illustrated in Figure 4.10, equation 4.37 approximates the area of a unit circle and permits the user to choose any large value of N, the number of triangles.
Table 4.2 shows a summary of answers for various values of N. The last two lines are the value of pi computed using a spreadsheet, π = 4 arctan(1.0), and the first twenty digits of π (Beckmann 1971).
TABLE 4.2
Approximations for π Based on Area of Unit Circle
|
Value of N |
Area of Corresponding Unit Circle (to 15 significant digits) |
|
100 |
3.13952597646567 |
|
1,000 |
3.14157198277948 |
|
10,000 |
3.14159244688129 |
|
100,000 |
3.14159265152271 |
|
1,000,000 |
3.14159265356913 |
|
10,000,000 |
3.14159265358959 |
Note: Spreadsheet computation: 4 * atan(1) = 3.14159265358979. First 20 digits of π: 3.1415926535897932385.
Comment: mathematicians have devised better ways of computing π, but this technique shows an interesting connection between the value of π and the area of a unit circle while illustrating the concept of limits.