Algorithm for Functional Model
A more complete set of equations and derivations is provided, but the following symbols are defined and used in this summary as follows:
X/Y/Z: Geocentric right-handed rectangular coordinates
AX/AY/AZ: Geocentric coordinate differences
Ae/An/Au: Local coordinate differences
φ/λ/h: Geodetic latitude/longitude (east) and ellipsoid height
a and b: Semimajor and semiminor axes of reference ellipsoid
f: Flattening of reference ellipsoid
e2: Eccentricity squared of reference ellipsoid; e2 = 2f – f2
N: Length of ellipsoid normal; also used for geoid height
S: Spatial slope distance between standpoint and forepoint
a: Geodetic azimuth at standpoint to forepoint
z or V: Zenith direction or vertical angle to forepoint
H: Orthometric height (elevation)
HD(I) or D: Ground-level horizontal distance
TABLE 1.1
Designations for Spatial Data Computations and Transformations
a BK5, BK6, and BK7 are quite similar, but having different designations will help avoid problems caused by the subtle differences.
Notes:
1. All distances are in units of meters.
2. Where two points are concerned, the standpoint is indicated by the subscript 1, while the forepoint is indicated by the subscript 2.
The BK1 equations are as follows:
The BK2 equations are more difficult to use because iteration is normally required to solve them. Equation 1.5 is quite straightforward, but equations 1.6 and 1.7 need to be iterated.An alternate (noniterative) method for performing the BK2 transformation is also given.
The BK3 and BK4 equations are also called the 3-D “forward” and “inverse” as shown here:
The BK5 computation handles any combination of orthometric height (H), ellipsoid height (h), and geoid height (N) as follows:
The BK6 computation is the same as BK5 except that differences are used as follows:
Differences are important because geoid modeling provides better answers when using relative geoid height differences rather than absolute geoid heights.
The BK7 computation relies on the combined curvature and refraction (c+r) correction for the difference between a level surface and tangent plane surface. For modest precision over short distances, the c+r correction can be used beneficially as follows (Davis et al. 1981, equation 5.7):
The BK8 and BK9 transformations involve using a rotation matrix to convert geocentric differences to local differences and local differences to geocentric differences.
The BK8 transformation of geocentric differences to local differences is:
The BK9 transformation of local differences to geocentric differences is as follows:
Equations 1.23 and 1.24 are not BKX transformations, but they are used to obtain the local tangent plane horizontal distance and the true direction from the standpoint (PTj) to the forepoint (PT2):
The BK10 and BK11 transformations are used to handle state plane coordinate transformations and are discussed.
BK12 computations are used to develop local tangent plane coordinates with respect to any P.O.B. selected by the user.
BK13 transformations are used to convert terrestrial observations into local coordinate differences that can then be converted to geocentric differences using the BK9 transformation. Such observations may need to be corrected for instrument calibration, atmospheric conditions, polar motion, and local deflection-of-the-vertical.
There is no one correct set of equations for BK14 and BK15 computations. The primary force behind the use of project datum (or surface) coordinates is that an inverse between grid coordinates (grid distance) is not the same as the horizontal ground distance.More recently, the concept of a low distortion projection (LDP) has been proposed, and the advantages of central
Σγγ = covariance matrix of computed result,
Σχχ = tcovariance matrix of variables used in computation, and
JYX = Jacobian matrix of partial derivatives of the result with respect to the variables.
The GSDM uses two covariance matrices for each point—the geocentric covariance matrix and the local covariance matrix. The geocentric covariance matrix is stored and the local covariance matrix is computed on an “as needed” basis. In particular, the following symbols and matrices are used in the stochastic model:
Notes about the individual point covariance matrices:
1. Each covariance matrix is 3 x 3 and symmetric. Six numbers are required to store upper (or lower) triangular values.
2. The unit for each covariance matrix element is meters squared, the off-diagonal elements represent correlations, diagonal elements are called variances, and standard deviations are computed as the square root of the variances.
3. Each covariance matrix (with its unique orientation) represents the accuracy of a point with respect to a defined reference frame (or to whatever control is held fixed by the user) and is designated datum accuracy.
The local covariance matrix and the geocentric covariance matrix are related to each other mathematically by a rotation matrix for the latitude/longitude position of a point computed from its X/Y/Z coordinates.
The relationship between the covariance matrices is as follows:
With regard to the rotation matrix in equation 1.31, longitude is counted 0° to 360° east from the Greenwich meridian, west longitude is a negative value, and latitude is counted positive north of the equator and negative south of the equator.
The GSDM 3-D Inverse
Given that point 1 is defined by X1/Y1/Z1 and point 2 by X2/Y2/Z2, matrix formulations of the 3-D geocentric coordinate inverse and covariance error propagation are as follows:
The Jacobian matrix from equation 1.34 and the general covariance error propagation procedure (equation 1.35) are used to find the overall geocentric inverse covariance matrix as follows:
Correlation between points 1 and 2 is described by the off-diagonal submatrices. Various accuracies are defined by a choice with regard to the use of the covariance matrix in equation 1.36. The matrix operation in equation 1.36 can be used to compute the following:
1. Local accuracy if the full covariance matrix is employed (relative accuracy based upon the quality of measurements connecting adjacent points)
2. Network accuracy if the correlation between points 1 and 2 is zero (relative accuracy based upon the combined quality of each point with respect to the network)
3. P.O.B. accuracy if the covariance matrix of point 2 is the only one used (relative accuracy based solely on the network quality of point 2)
Equation 1.36 is really the heart of the stochastic model portion of the GSDM. Yes, equations 1.32 and 1.33 can be used to convert absolute datum accuracy from one reference frame to another (geocentric and local), but, when looking at one point with respect to another, equation 1.36 offers important choices in answering the question “Accuracy with respect to what?” If a connecting measurement between two points has a smaller standard deviation than would be computed given no correlation between them, then the local accuracy of one point with respect to the other can be computed with statistical reliability. These tools give the spatial data user a number of choices and the option of computing the standard deviation of all subsequently derived quantities such as distance, direction, height, volume, and area.
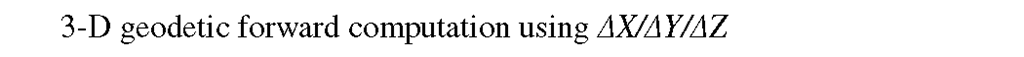
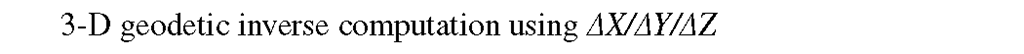
![tmp7f94-7_thumb[2] tmp7f94-7_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f947_thumb2_thumb.png)
![tmp7f94-8_thumb[2] tmp7f94-8_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f948_thumb2_thumb.png)
![tmp7f94-9_thumb[2] tmp7f94-9_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f949_thumb2_thumb.png)
![tmp7f94-10_thumb[2] tmp7f94-10_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9410_thumb2_thumb.png)
![tmp7f94-11_thumb[2] tmp7f94-11_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9411_thumb2_thumb.png)
![tmp7f94-12_thumb[2] tmp7f94-12_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9412_thumb2_thumb.png)
![tmp7f94-13_thumb[2] tmp7f94-13_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9413_thumb2_thumb.png)
![tmp7f94-14_thumb[2] tmp7f94-14_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9414_thumb2_thumb.png)
![tmp7f94-15_thumb[2] tmp7f94-15_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9415_thumb2_thumb.png)
![tmp7f94-16_thumb[2] tmp7f94-16_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9416_thumb2_thumb.png)
![tmp7f94-17_thumb[2] tmp7f94-17_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9417_thumb2_thumb.png)
![tmp7f94-18_thumb[2] tmp7f94-18_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9418_thumb2_thumb.png)
![tmp7f94-19_thumb[2] tmp7f94-19_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9419_thumb2_thumb.png)
![tmp7f94-20_thumb[2] tmp7f94-20_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9420_thumb2_thumb.png)
![tmp7f94-21_thumb[2] tmp7f94-21_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9421_thumb2_thumb.png)
![tmp7f94-22_thumb[2] tmp7f94-22_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9422_thumb2_thumb.png)
![tmp7f94-24_thumb[2] tmp7f94-24_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/07/tmp7f9424_thumb2_thumb.png)

