Sphingolipid Models and Their Potential Uses
Over a span of several years, we have been developing a series of increasingly more sophisticated models of sphingolipid metabolism.13,14,24,25 The models were formulated as systems of nonlinear ordinary differential equations in the format of power-law functions, as suggested in BST.18 Choosing this framework, it was straightforward to set up symbolic equations that reflect the known or assumed connectivity and regulatory signals of the pathway system. While this part of the model design phase was manageable with reasonable effort, the estimation of suitable parameter values was very challenging. Indeed, our case study confirmed common experience that parameter estimation is the bottleneck of biological modeling. In our case, the estimation was based on literature information, de novo experiments and some default assumptions based on experience with BST.14 The resulting model was subsequently tested in the typical fashion, namely with stability, sensitivity and robustness analyses, through comparisons with experimental data that had not been used in the estimation phase and through qualitative reality checks based on biological experience. After many iterations and revisions, the model appeared reasonable and was semi-quantitatively validated with additional wet experiments.13
It would be counterproductive to use the limited space of this topic to review the steps of a typical modeling process in general or even within the context of sphingolipid metabolism, because both have been described in recent years and at various levels of sophistication and detail (for example see refs. 10, 14, 18, 24). Instead, it seems more beneficial to ask what we may do with such models, once they are validated. Again, many typical uses of models have been described in the literature and we will simply mention some of them. However, other uses are less typical and will receive more attention in the following.
The first and foremost role of a mathematical model is the integration of diverse data and other pieces of information, such as kinetic characteristics of enzymes, expression profiles of genes, protein abundances and maybe even semi-qualitative clinical observations. This integration often shows very clearly whether we have a good grasp of the functionality of the pathway, because most initial efforts of merging all information into one mathematical construct fail. Typical failures become apparent in lacking stability or robustness of the model that is accompanied by unduly high sensitivities. In the former case, small variations in input or in some variable may cause the model to "crash" in a sense that one or more variables vanish. In the latter case, the system "overreacts" to small changes in parameters. For instance, a 5% increase in some enzyme activity could lead to a 220% increase in some metabolite, which is unreasonable in most cases. Relatively straightforward diagnostic tools weed out such systems (for example, see ref. 18).
If a model appears reasonable, we can further test our intuitive grasp of the system through simulation studies that represent What-If scenarios, as we employed them before. For example, the reduction in an enzyme activity is easily implemented in the model and simulation results can possibly be validated with wet experiments. An integrated model of sphingolipid metabolism also allows us to follow the fate of metabolites of interest, many of which are recycled or involved in several reactions. A good model, with slight adaptations, even permits the tracking of labeled substrates, from input to their ultimate fates.10,14 As a variation on this theme, a reliable model may be used to study the relative contributions of different pathways to a common goal, such as the formation of rafts that become structural elements of membranes.
In a study of a slightly different nature, we asked the question whether a yeast cell mounts a response to stress by up-regulating a small number of enzymes (genes) a lot or whether it changes the activities of many enzymes a little bit. Intuitively one could easily find rationale for either strategy. On one hand, up- or down-regulating only one or two genes or enzymes appears to be the simpler strategy. On the other hand, drastic changes in some part of the pathway could lead to concomitant and undesired side effects. In our test case of the diauxic shift, the modeling analysis suggested that many enzymes are involved in the response.24
Sphingolipid metabolism has been analyzed experimentally in different organisms, some of which are phylogenetically close. This similarity permits the cautious extrapolation and use of the model in an untested organism. This type of model transfer was demonstrated by using the original S. cerevisiae model with some adaptations to study sphingolipid metabolism in Cryptococcus neoformans (Cn), an airborne fungal pathogen that may cause life-threatening infections.25 The main challenge this organism faces is the distinct difference in pH between alkaline or neutral extracellular environments.The model results together with subsequent validation studies led to the very specific proposition that inositol phosphoryl ceramide synthase (Ipc1) and inositol sphingolipid phospholipase C (Isc1) affect the function of the plasma membrane H+-ATPase pump (Pma1) through modulation of the level of phytoceramides and complex sphingolipids.25
The successful use of the yeast model in the investigation of a fungal pathogen suggests that it might even be possible to study the evolution of design principles governing sphingolipid function, based on comparative model analyses of sphingolipid metabolism in closely related and more distant species. Along the same lines, a major future project should convert and test the yeast model for analyses of the mammalian analogues. This "extrapolation" is much more complicated, because mammalian sphingolipids are often bound to carbohydrates, which leads to a multiplication in the number of potentially relevant compounds, as discussed before.28 This explosion in number may appear overwhelming for a model analysis. However, trying to understand the mammalian systems without computational approaches seems to be incomparably more complicated. It is clear that a mammalian model could be very useful for the exploration of pathways leading from health to diseases such as cancer, where we have strong indication that sphingolipids are involved (for example see ref. 29).
As a first step toward comparative studies, the sphingolipid system of the same organism may be studied at different grades of granularity. For instance, our present yeast model accounts only partially for compartmentalization. As a next step, it might be fruitful to distinguish sphingolipids and precursors with different fatty acid chain lengths. Accounting for this detail will require a substantial increase in model size and require additional biological information about the relevant compounds of different sizes and their respective roles.
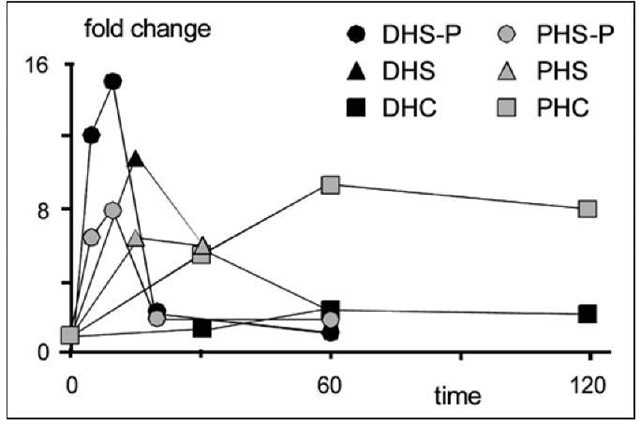
As a more detailed example of an atypical model investigation, consider the immediate sphingolipid response in yeast to heat stress. Genome studies have strongly supported the involvement of several genes, such as MSN2/4 and YAP1.30 However, preliminary concentration measurements of key sphingolipids indicate that the heat stress response is much faster than any gene-regulatory mechanism could accomplish, exhibiting metabolic changes within a few minutes (Fig. 331; and Y.A. Hannun, pers. comm.; see also ref. 32). Within about 8 minutes, dihydrosphingosine-phosphate (DHS-P) and phytosphingosine-phosphate (PHS-P) increase to 8- and 15-fold levels, respectively, before resuming almost normal values after about 20 minutes. DSH and PSH respond more slowly, peaking after about 15 minutes at 6- and 11-fold levels. Phytoceramide accumulates gradually over a period of about an hour, peaking at a level that is about 8 times higher than baseline. Dihydroceramide shows the same pattern, but with a peak accumulation of only about two-fold.
Figure 3. Fold changes in sphingolipids following heat stress at time t = 0. Abbreviations: DHS: dihydrosphingosine; PHS: phytoshpingosine; DHC: dihydro-ceramide; PHC: phyroceramide; -P: -phosphate.
This fast change in metabolic profile is intriguing and not explainable with gene regulatory actions. We have seen a similarly quick response to heat stress in the trehalose cycle in yeast, which, according to careful in vivo NMR measurements, begins producing trehalose within two minutes.30 Again, a gene regulatory response is too slow for such a response. As it turned out in the trehalose case, three key enzymes of the trehalose pathway are heat sensitive. The two enzymes controlling trehalose production are more active at higher temperatures, while trehalase is less active.33 A preliminary mathematical model analysis suggests that the relatively slight changes in activity are sufficient to mount the fast, observed response.30
Given the similarity of the heat response task in the case of trehalose and sphingolipids it is reasonable to ask whether there are heat-sensitive enzymes within the sphingolipid pathway as well. If so, would a single enzyme be sufficient to mount the observed sphingolipid response ? Would combinations of two or more enzymes be sufficient?
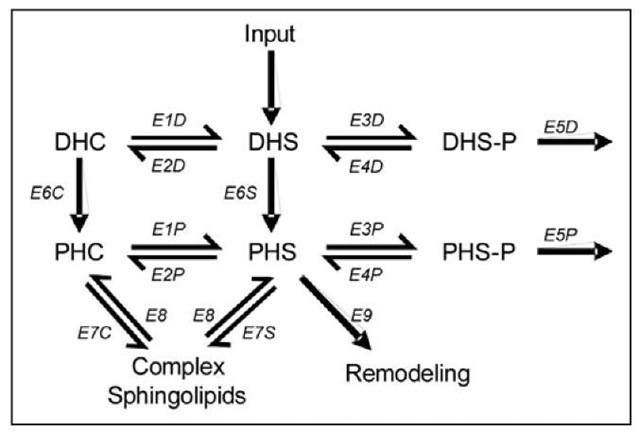
A mathematical model might help us identify such enzymes. First, it would of course be possible to launch a major simulation study, changing one or a few enzymes at a time and then testing whether metabolic concentration patterns like the one observed can be generated. However, some prudence might help us prescreen some possibilities and favor or disfavor particular hypothetical scenarios. To permit an objective, yet lucid exploration, we reduced the sphingolipid system to a minimum and converted it into a much simplified mathematical model. Thus, consider the reduced core of sphingolipid metabolism that contains only those components that appear most important (Fig. 4).
Looking at once at Figures 3 and 4, we can formulate the following as a framework for preliminary hypotheses. The concentration of phytoceramide at one to two hours exhibits a sustained level at eight times its baseline. This increased level requires that: (1) more material is produced per biosynthesis or recycling of complex sphingolipids (cf); (2) material is simply reorganized within the pathway system; (3) the loss of sphingolipids is reduced; or (4) several of the previous options are combined.
Figure 4. Reduced and simplified diagram of parts of the sphingolipid pathway involved in heat stress response. Abbreviations of metabolites are presented in Figure 3. Names of enzymes are not of relevance, but can be found in.14 E7C, E7S and E8 are collective representations for the interactions between the simple and complex sphingolipids.
The second option may be discarded off-hand: A simple reorganization or shift of fluxes in the neighborhood of DSH and PSH would require decreased levels of the substrates of these reactions, but decreases in concentrations are not observed. Although some of the biosyn-thetic genes are affected by heat, the first option alone also seems questionable, because DSH-P and PSH-P respond most quickly, whereas one would expect a response through increased biosynthesis to cause increases in DHS and PHS first. Besides, if PHC is the target and biosynthesis was the mechanism, why should DSH-P and PSH-P be increased at all? Similar arguments seem to hold for the recycling of complex sphingolipids. One could surmise that a direct change in E7C and/ or E8 could be a good strategy toward an increased level of PHC. However, this is apparently not a strategy pursued by the cell. Pursuing the third (or fourth) option, the observed metabolite profile could possibly be achieved through a reduction in the lyase reaction (E5D, E5P), which would lead to an accumulation of the phosphorylated forms. This change would have to be followed by increased sphingoid base PPase (E4D, E4P) and hydroxylase (E4D, E4P) activity, which would gradually shift the increasing amounts of DSH-P and PSH-P toward the dephosphorylated forms and from there to ceramide (E6C, E6S). It is interesting to note that the dihydro- and the phyto-forms of sphingolipids essentially form parallel pathways, but that the target profile after heat stress is distinctly different between the two pathways. This observation suggests that the involved enzymes might have different affinities for the dihydro- and the phyto-forms, at least under heat stress conditions.
Complex systems have a way of tricking our intuition and our hand waving arguments could simply turn out to be wrong. Nevertheless, it is possible to test these scenarios with a model. In order to keep our exploration as simple as possible, we created a reduced model reflecting the simplified pathway shown in Figure 4; it is shown in Eq. (3). Because the only purpose of this model is a proof of concept showing whether or not changes in enzyme activities could lead to something like the observed metabolite profile, we set the model up in a minimalistic fashion, again using (almost arbitrary) default parameter values and enzyme activities set to a nominal value of 1, so that the steady state consists of unity values. These intentional simplifications may show us the consequences of introduced changes more clearly than a model that is parameterized from actual data, but of course we cannot expect to obtain numerically valid simulation results.
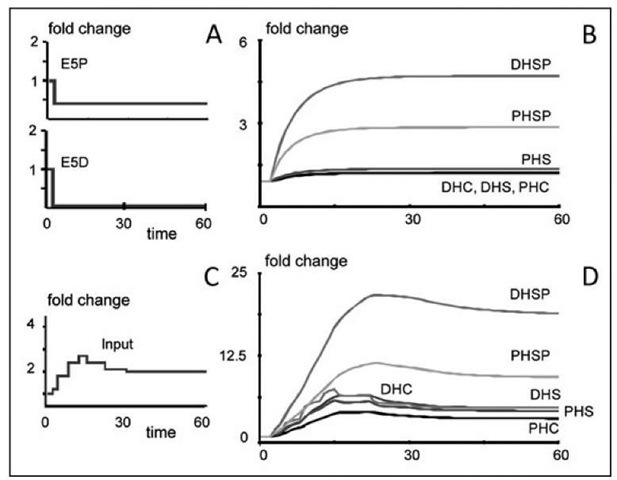
As a first simulation, we start the model at the steady state (1, …, 1). Because all values are 1, all later results automatically represent "fold" changes. At time t = 2, we reduce the lyase activity (E5D, E5P) (Fig. 5A). Even with different magnitudes and different changes for the lyases with respect to DHS-P and PHS-P, the resulting sphingolipid profiles are not even close to the observations in Figure 3; instead, they primarily lead to accumulation of DHS-P and PHS-P (Fig. 5B).
For a second exploration, we double the (biosynthetic) input starting at t = 2. The result is increased mass in the system, but the resultant profile is similar to that in Figure 5B (results not shown). As a variation on the same theme, we increase the input more gradually and assume that after a while the substrates for biosynthesis become limiting, thereby reducing the input flux (Fig. 5C). The model now yields a peaking profile, but all metabolites respond in parallel (Fig. 5D).
Figure 5. Two simulation scenarios with Equation (3) exploring the feasibility of simple changes in enzyme activities. A) The two lyases are reduced two minutes after initiation of heat stress. As a consequence (B), the phosphorylated sphingolipids accumulate. If in addition the input to the system changes in direct response to heat, the same metabolites increase more. Assuming that increased biosynthesis leads to substrate deprivation, the sphingolipid profiles begin to decrease.
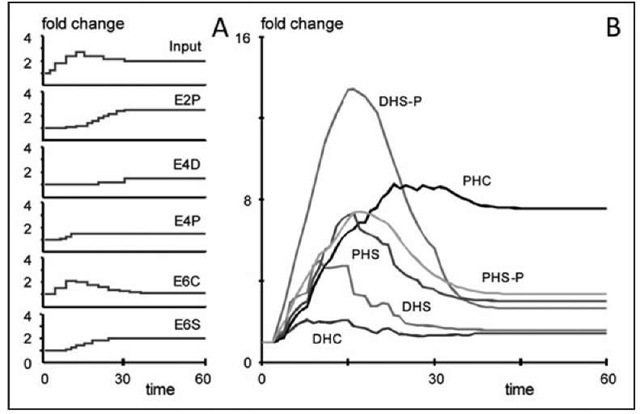
Figure 6. Simulation scenario with Equation (3) in which several enzymes have temperature dependent activities. Profiles of changes in enzymes and input are given in (A); see Figure 3 for abbreviations. The corresponding sphingolipid profiles show a qualitatively similar pattern as it was observed (Fig. 4). The "jagged" appearance of the simulated profiles is due to discrete changes in enzyme activities.
Uncounted simulations of this type may be executed and in the end it would be wise to formulate an optimization program that would guide the progression of simulations. Through manual exploration, we developed a more complex heat stress response pattern in enzyme activities (Fig. 6A) that actually produces a metabolic profile that qualitatively resembles the observations (Fig. 6B). This profile is clearly not unique and not refined or optimized, because it is based on the simplified model with "invented" parameter values, rather than a fully parameterized model. Nonetheless, the simulation constitutes proof of concept that temperature dependent enzymes could be the drivers of the very fast sphingolipid response to heat, as it is the case in the trehalose cycle. Interestingly, "successful" profiles like the ones in Figure 6A seem to require different affinities of the enzymes to the dihydro- and phyto-forms of the metabolites.
In addition to simulation studies, the model format of an S-system within BST could be used to exhaust all possible means of achieving a desired profile at steady state. We have shown in a completely different context how such an analysis could be pursued10 (see also ref.19). In a nutshell, the mathematical features of the S-system model allow an elegant algebraic analysis of the entire space of steady-state solutions in terms of enzyme activities that are consistent with a desired metabolic concentration profile. Among these consistent solutions, optimal transient solutions could be determined through dynamic analyses or nonlinear optimization studies.
Conclusion
The pathways of sphingolipid biosynthesis, utilization and recycling form an intriguingly complex system whose dynamics is difficult to predict with intuition alone. Mathematical modeling provides an aid in this regard, because it permits the integration of many pieces of information into computational structures that are very easy to diagnose, interrogate and analyze through What-If simulations. The bottleneck of setting up such models is the determination of parameter values, which may be based on literature information characterizing genes, enzymes and metabolites in a steady-state situation, or on dynamic time trends, which can be measured with modern methods of mass spectrometry or nuclear magnetic resonance. Parameter estimation is the bridge between wet experimentation and modeling and the need for improved parameter values, which are valid in vivo and under relevant physiological conditions, gives clear indication that mathematical modeling is crucially dependent on solid experimental work. At the same time, once reliable models are established, they become incomparably rich tools for analyses that are often unattainable with wet experimentation. For instance, it is at least theoretically feasible to determine all possible combinations of enzyme activities that lead to an observed metabolite profile at steady state. As we indicated here with an intentionally simplified analysis, it is also possible in principle to determine mathematically which enzymes would have to altered and in what manner, to obtain dynamic metabolite profiles as they are observed in responses to perturbations such as heat stress.
Ultimately, reliable mathematical models will be used as valuable tools for exhaustive prescreening studies for all kinds of scenarios and for creating novel and optimally discerning hypotheses that are then to be tested in the laboratory. If the history of physics is an indication of the future of biology, we might one day execute experiments only once the theory describing the underlying system is sufficiently worked out and understood. Even if this procedure will become the norm in the future, one must expect that it will take many years and dedicated effort, both experimentally and methodologically, to establish models of sufficient scope and reliability. Thus, the rise of mathematical modeling as a biological technique should not be seen as threatening to experimentation, but simply as an additional tool that is able to elucidate different aspects of a system. Modeling has improved tremendously over the past decades and successful collaborations between biological and computational scientists in the recent past have begun to show that their team efforts will be rewarding to both sides and reveal insights that neither side could have obtained without the other.
![tmp10-19_thumb[2] tmp10-19_thumb[2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp1019_thumb2_thumb.jpg)