ABSTRACT
In-situ tensile tests have been carried out during X-ray microtomography imaging of dual-phase steels. Void nucleation has been quantified as a function of strain and triaxiality using the obtained 3D images. The Argon’s criterion of decohesion has then been used in a model for nucleation in the case where martensite plays the role of inclusions. This criterion has been modified to include the local stress field and the effect of kinematic hardening present in such an heterogeneous material.
Introduction
Ductile damage is characterized by a three step process: cavities first nucleate, then grow, until coalescence leads to the ductile fracture. The first step of nucleation has been extensively studied and modeled. Void nucleation is usually associated to the presence of a second phase, like particles or inclusions. In the latter case, the cavities appear close to the inclusions, either inside the particle or at the interface [1-3]. Dual-Phase steels (DP steels) containing hard martensite islands embedded in a ductile ferritic matrix, are such kind of materials promoting inhomogeneous nucleation. In DP steels, the main nucleation mechanism is the interface decohesion as experimentally observed by [4, 5]. To model this interface debonding, an energy criterion [2,6,7] is necessary for the creation of new surfaces and a stress criterion [1,8] or a strain criterion [9,10] is required for breaking the bonds. To combine the two criteria, numerical models using cohesive zones have also been developed [1113].
In order to be validated, these models have to be compared with key experiments. X-ray absorption microtomography is currently one of the most reliable ways to obtain quantitative three-dimensional (3D) information on damage [14,15]. In the present paper, damage in a DP steel is studied by in-situ tensile tests during X-ray microtomography imaging. Quantitative data is then used to validate an analytical modeling of void nucleation based on the Argon’s criterion [1].
Experimental procedure
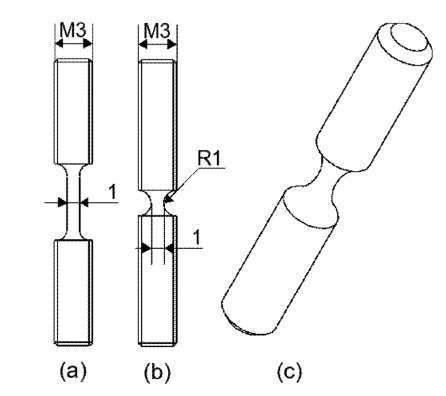
X-ray microtomography has been used in the present study to quantify damage during in-situ tensile tests. The method can be used for the imaging and the quantification of the microstructure of materials. Applications to study damage in ductile materials can be found in Refs. [14-16]. The tomography setup used is the one located at the ID15 beam line at the European Synchrotron Radiation Facility (ESRF) in Grenoble, France (more information is given in [17]). Tomography acquisition is carried out with a voxel size of (1.6^m)3. With such a resolution, the smallest observed voids have a diameter of almost 2^m. Smaller voids, not accounted in the quantification, do exist in the sample but may not play a major role in damage. The DP steel used for this study was cut from a 3 mm thick sheet obtained by hot rolling and thermal treatment. Its mechanical properties are given in Table 1. It has been checked by image analysis of optical micrographs of polished surfaces that the steel contains about 11% martensite. Axisymetric specimens were machined from the original sheet. Two kinds of specimen’s shapes inspired by [18] were cut: two smooth samples and two samples with a 1 mm notch radius. The specimen’s geometry is given in Fig.1. Each shape induces a different initial triaxiality. This allows us to study the effect of this important parameter on damage. Only the central part, 1.6 mm in height, is imaged during the present study.
Table 1 Mechanical properties in tension of the studied DP steel
|
Re (MPa) |
Rm (MPa) |
Ag (%) |
A (%) |
|
366 |
603 |
17.7 |
26.6 |
The fractured samples were polished after the in situ tensile test down to their central plane and etched with a 2 pct nital solution. The samples were dipped in a solution of ethanol and placed into a ultrasound cleaner for a duration of 30 minutes after the polishing to eliminate the possible fragments blunting the cavities. Light optical micrographs were then acquired in order to observe the nucleation sites.
Fig.1 Tensile samples used: smooth specimen (a), 1mm radius notched specimen (b), 3D view (c)
Results and discussion
Damage characterization
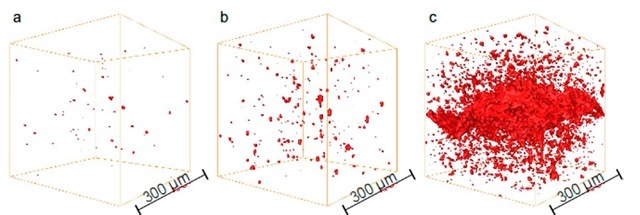
X-ray microtomography imaging has already been used in order to visualize and quantify damage in DP steel in [17]. The same procedure was used in this study: raw processing were performed with the ImageJ freeware [19]. Initial volumes were median filtered and simply thresholded to differentiate material from voids. Damage can be qualitatively observed in 2D using sections inside the volume as ones presented in Fig.2 or in 3D using a global view of the sample as ones showed in Fig.3. 3D visualization softwares allow one to have a transparent view of some of the voxels (for instance those located in the solid phase) and then lead to the possibility of seeing cavities inside the sample. Tomography volumes can also be employed to quantify damage appearing during the tensile test. As in [17], only the central part of the tensile specimen is used for this damage quantification. This sub-region was chosen to be a cubic volume of (300^m)3. Fig.4. shows this studied sub-region in a notched specimen of DP steel at several steps of deformation. This qualitative figure shows clearly that the number of cavities increases (nucleation) and that the size of the nucleated cavities also increases (growth) with the increase of strain. It is noticeable in this image that nucleation is a quantitatively important part of the damage progression in these materials, as evidenced already in [17]. Each pore of the volume is then subsequently labeled using a dedicated image processing plugin implemented in the ImageJ [19] freeware. The labeling plugin uses a binary image as input. It simply detects the 3D clusters of connected voxels and gives a label to each. The void density is calculated as the number of cavities per cubic millimeter in the sub-volume. The volume of each cavity is also measured as well as its dimensions permitting to quantitatively characterize the growth and the shape change of voids during the tensile deformation.
Fig.2 Sections at the center of a notched strained specimen at various steps of deformation:
Fig.3 3-D views of a notched strained specimen at various steps of deformation:![]() The outline of the specimen appears in gray and the cavities in red
The outline of the specimen appears in gray and the cavities in red
Fig.4 3-D views of damage at the center of a notched strained specimen at various steps of deformation:![]()
![]()
Some mechanical parameters were calculated using the outside shape of the specimen. The minimal section area S was measured in order to calculate the local strain etoc at each step using equation (1):
So being the initial section of the sample. This equation implies that the effect of porosity in the volume change of the sample is neglected in our analysis.
The curvature radius R„otch is also measured in order to determine the stress triaxiality T using equation (2), derived from the Bridgman analysis of notched bars [20].
a being the radius of the minimal section, easily tractable from the value of S.
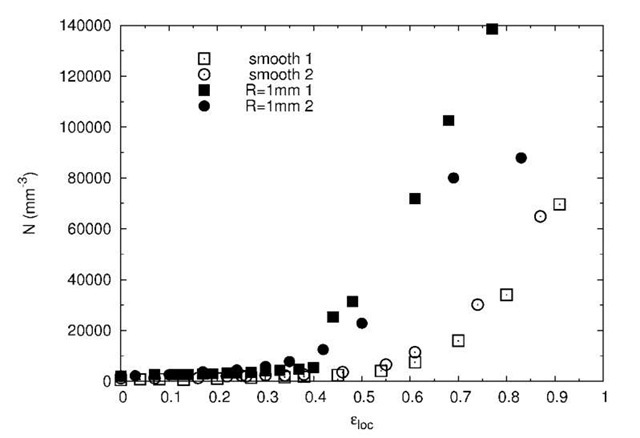
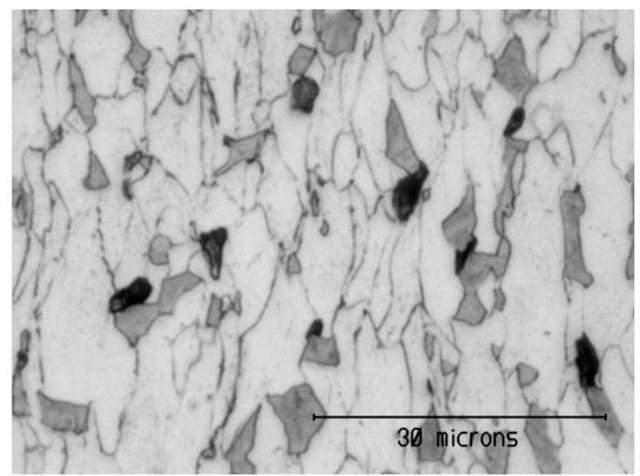
Fig.5. shows the evolution of N, the number of voids per unit volume (expressed per cubic mm) in several DP steel samples with smooth and notched geometries. A very small amount of porosity (0.03%) can be detected before the tensile test, may be due to the fabrication process. The experimental results show that the triaxiality has a straightforward impact on the nucleation kinetic: void nucleation occurs earlier in notched samples inducing higher triaxiality than in smooth samples. Optical micrographs performed on the fractured specimens and given in Fig.6. show that most cavities are localized between the ferritic matrix and martensite islands and thus nucleate by decohesion of the ferrite/martensite interface as previously observed in [4, 5].
Fig.5 Evolution of N, the number of cavities per cubic mm in the four studied samples measured during the in-situ tensile tests.
Fig.6 Micrograph of fractured specimen. Voids appear in black, ferrite in light gray and martensite in dark gray.
Void nucleation modeling
As demonstrated by [6], the energy criterion necessary for the creation of new surfaces at the inclusion/matrix interface is satisfied at the onset of plastic deformation in materials containing inclusions bigger than about 25 nm in diameter. Only a stress criterion will therefore be used to model the interface decohesion in DP steels as the observed inclusions are about 100 times larger than this. The Argon’s criterion [1] is a critical stress criterion stating that the void nucleation occurs when a critical stress state, necessary for the interface decohesion, is reached in the material. This stress state involves a contribution of the hydrostatic stress am and the equivalent stress aq
where ac is the interface strength, e.g. the maximum shear stress that the interface can support without breaking.
The interest in using the Argon’s criterion lies in the fact that it accounts for the triaxiality T (T being the ratio between aeq and am ).
Combining Eq. (3) and Eq. (4), the criterion can be expressed as:
In the original Argon’s criterion, the triaxiality used is the macroscopic triaxiality. However, decohesion is a local phenomenon which occurs at the interface of ferrite and martensite islands. In [22], it is demonstrated that the local triaxiality is higher at the interface because of the kinematic hardening X generated by the difference in mechanical behaviors of both phases. In DP steels, the difference between the mechanical behavior of the ferrite and martensite is quite high. Therefore it would be better to use the local triaxiality at the interface Thc. To$ can be estimated using the following expression coming from [22]:
The modified expression of the Argon’s criterion to get a local decohesion then becomes:
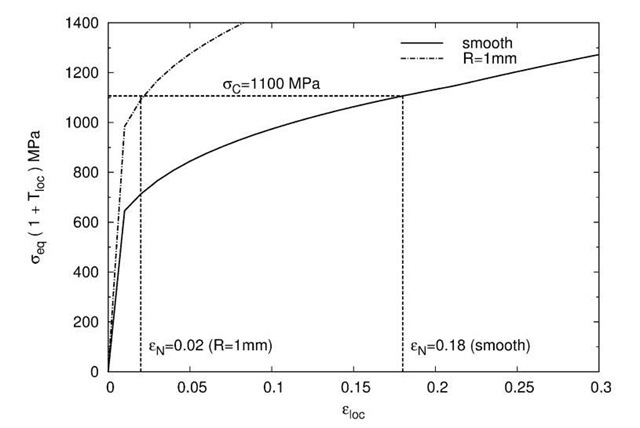
The left side of the equation of this local version of the Argon’s criterion is hereafter named % By calculating the value of % at the nucleation strain eN, an average value of oc can be estimated in the case of ferrite/martensite interface. £n is determined from the quantitative data obtained from the cavity measurements of the smooth samples. Its value is taken at the point when the void density starts to increase. Values of 0.18 and 0.02 are respectively found for the smooth samples and the notched samples. aeq is taken from the experimental true stress tensile curve and T is calculated with the Bridgman formula [20]. The value of the kinematic part of the hardening X is estimated from the formula given by [24] and modified to be expressed as a function of the respective hardness of ferrite HVf and martensite HVm:
where fm is the volume fraction of martensite. Assuming that all the carbon present in the studied DP steel is located in the martensitic phase, the carbon content of the martensite is 0.73 wt.%. Regarding the work done by Grange on the prediction of martensite hardness [24], the value of HVm is about 830 MPa. The hardness of the ferritic phase is taken as 150 MPa. The evolution of x in the smooth and in the notched specimen with the deformation is given in Fig.7. The value of the interface’s strength found here for this particular value of strain when nucleation starts to increase is equal to about 1100 MPa. A compilation of values for the strength of the interface between other particles and ferrite found by different authors is listed in Table 2. The order of magnitude is the same as the one calculated using our approach, the case of ferrite/martensite being situated in the lower range of these values. Note that our estimation is valid for the very beginning of the nucleation (i.e. when the number of voids starts to increase as seen in the tomography images). The other values being obtained with other methods and probably with other definitions, a direct comparison is not the aim of the presented table.
Fig.7 Calculation of the ferrite/martensite interface using %
Table 2 Value of ferrite particle interface strength
|
Particle |
Interface strength (MPa) |
Ref. |
|
Y2O3 |
1000-1600 |
[251 |
|
MnS |
1100-1400 |
[26] |
|
Fe’C |
1200-2000 |
[27,280 |
As pointed out in [5], void nucleation in DP steels occurs during the entire deformation process, i.e. each different single interface probably exhibits a different value of £N and each interface is possibly subjected to a scattered value of x Interface decohesion is thus a progressive phenomenon, starting for a strain of 0.18 (in smooth specimens) but continuing after this value of strain and the evolution of the cavity density has to be modeled as a function of the local strain. Fig.5 shows that the studied material exhibits two different nucleation regimes at low and at high strain. Firstly, the number of cavities increases slowly and linearly. In a second regime many voids appear exponentially. This experimental observation leads us to propose the following empirical equation based on the local criterion of decohesion and involving the parameters x and ac.
A and No being two constants (expressed in the same unit as N, for instance in mm-3).
The two extreme regimes are well described by this empirical expression. When N N0 the following approximation can be done:
The interface decohesion is then only linearly controlled by the local stress x which increases with the applied strain. In the second regime, when N ^ N0 the approximation becomes :
The evolution rate of N with strain is proposed to depend on N itself, transcribing a self catalytic effect and thus the exponential acceleration of the number of cavities.
We then now have a mean to integrate the value of N, by accounting for the local triaxiality at the interface. The assessment of the model is firstly done using experimental data from smooth specimens. The values of the two constants A and No giving the best fit between modeling and experimental data for the smooth sample are A=4500mm-3 and No= 1250mm-3. These values, when used in the framework of the notched samples, also show a satisfactory agreement as shown in Fig.8. This validates that using a local value of the triaxiality as a driving force in an interface fracture criterion is a reasonable procedure.
Fig.8 Comparison of the prediction of the nucleation model and experimental data [21]. The constants of the model are fitted to reproduce the experimental evolution in the case of the smooth sample and are then used "as-is" to calculate the evolution of the notched sample.
Conclusions and perspective
Using in-situ tensile tests during X-ray tomography, the present study has shown that it is possible to obtain quantitative information about damage. Concerning the sites of nucleation, optical micrographs of fractured samples have shown that most cavities appear by decohesion of the ferrite/martensite interface. A value of the critical interface strength (1100 MPa) has been estimated for the onset of nucleation. The evolution of the void density has then been modeled according to an analytical approach based on a local version of the Argon decohesion criterion and accounting for the triaxiality. The model has been fitted with the experimental data on the smooth samples. The identified parameters were then used for the notched sample and also lead to a satisfactory agreement of the predicted evolution of the number of nucleated cavities. Some improvements could be foreseen in the present approach, particularly concerning the value of the interface strength in DP steels. This strength probably depends on the carbon content in the martensite and on an eventual tempering. These effects have to be investigated in more details before being modeled.


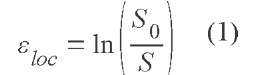
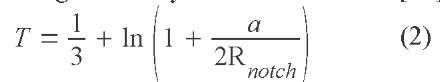
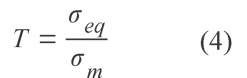
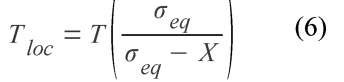
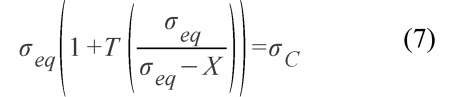
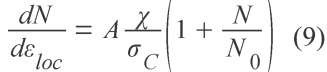
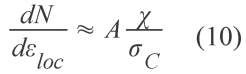
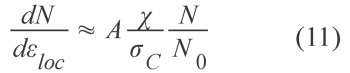
![Comparison of the prediction of the nucleation model and experimental data [21]. The constants of the model are fitted to reproduce the experimental evolution in the case of the smooth sample and are then used "as-is" to calculate the evolution of the notched sample. Comparison of the prediction of the nucleation model and experimental data [21]. The constants of the model are fitted to reproduce the experimental evolution in the case of the smooth sample and are then used "as-is" to calculate the evolution of the notched sample.](http://what-when-how.com/wp-content/uploads/2011/07/tmp1138_thumb_thumb.jpg)
