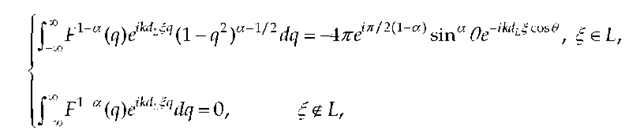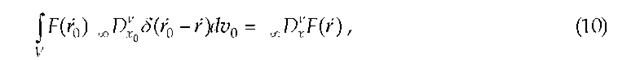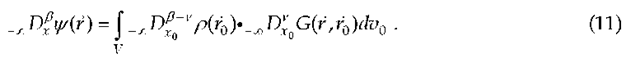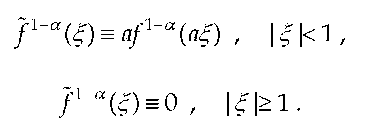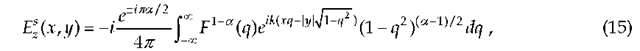Introduction
Tools of fractional calculus including fractional operators and transforms have been utilized in physics by many authors (Hilfer, 2000). Fractional operators defined as fractionalizations of some commonly used operators allow describing of intermediate states. For example, fractional derivatives and integrals (Oldham & Spanier, 1974; Samko et al., 1993) are generalizations of derivative and integral. Fractional curl operator defined in (Engheta, 1998) is a fractionalized analogue of conventional curl operator used in many equations of mathematical physics. A fractionalized operator generalizes the original operator. The idea to use fractional operators in electromagnetic problems was formulated by N. Engheta (Engheta, 2000) and named "fractional paradigm in electromagnetic theory". Our purpose is to find possible applications of the use of fractional operators in the problems of electromagnetic wave diffraction. In this paper two-dimensional problems of diffraction by infinitely thin surfaces are considered: a strip, a half-plane and a strip resonator (Fig.1). Assume that an incident field is an E-polarized plane wave, described by the function
where 0 is the incidence angle, 
is the wavenumber.
Fig. 1. Geometry of the diffraction problems: a) strip, b) half-plane, c) two parallel strips.
Here, the time dependence is assumed to be e-at and omitted throughout the paper. There are three structures considered in this paper:
- a strip located in the plane y = 0 (x e [-a, a]) infinite along the axis z (Fig. 1a);
- a half-plane (y = 0 , x > 0) (Fig. 1b);
- two parallel strips infinite along the axis z (a strip resonator). The first strip is located at y = l, x e [-a, a], and the second one is at y = -l, x e [-a, a] (Fig. 1c).
One may ask what new features are that the fractional operators can bring to the theory of diffraction. The concept of intermediate states, obtained with the aid of fractional derivatives and integrals, yields to various generalizations of commonly used models in electrodynamics such as:
• Intermediate waves. For instance, intermediate waves between plane and cylindrical waves (Engheta, 1996, 1999) can be obtained using fractional integral of scalar Green’s function:
where G2 is two-dimensional Green’s function of the free space. Ga describes an intermediate case between one- and two-dimensional Green’s functions and have the following behavior in the far-zone (Engheta, 1999):
This function consists of two waves: a cylindrical wave and a non-uniform plane wave propagating in the x direction and behaving with y as | y |a-1.
• Fractional Green’s function Ga defined as a fractional derivative (integral) of the ordinary Green’s function of the free space – Ga =-m DayG . a denotes the fractional order and varies from 0 to 1 (0<a< 1). In two-dimensional case Ga is expressed as
• Fractional Green’s theorem which involves fractional derivatives of ordinary Green’s function and fractional derivatives of the considered function on a boundary of a domain (Veliev & Engheta, 2003). The corresponding equations will be presented later in this paper.
• Fractional boundary conditions (FBC) defined via fractional derivatives of the tangential electric field components U(x, y). For an infinitely thin boundary S located in the plane y = d, FBC are defined as
The order of the fractional derivative a is assumed to be between 0 and 1. Fractional derivative Da is applied along the direction normal to the surface S . Fractional boundary conditions describe an intermediate boundary between the perfect electric conductor (PEC) and the perfect magnetic conductor (PMC), obtained from FBC if the fractional order equals to 0 and 1, respectively.
We will use the symbol Day f to denote operator of fractional derivative or integral _m D^f, which is defined by the integral of Riemann-Liouville on semi-infinite interval (Samko et al., 1993):
where T(1 -a) is Gamma function.
This paper is devoted to the problems of diffraction by a strip, a strip resonator and a half-plane characterized with fractional boundary conditions with 0 < a < 1 expressed as
where L = (-a, a) for a strip and L = (0,®) for a half-plane. For convenience, fractional derivative is applied with respect to dimensionless variable ky . The function Ez (x, y) denotes z-component of the total electric field, Ez (x, y) = E’z + Esz, that is the sum of the incident plane wave E’z (x, y) and the scattered wave Esz (x, y).
In case of a strip resonator we have two equations to impose fractional boundary conditions:
From the one hand, introduction of new boundary conditions should describe a new physical boundary world, and from the other hand they must allow to build an effective computational algorithm to solve the stated problems with a desired accuracy. Simple mathematical description of the scattering properties of surfaces is a common problem in modeling in diffraction theory.
One of the well-studied boundaries, which can be treated as an intermediate state between PEC and PMC, is an impedance boundary defined by the equation
where n is the normal to the surface S . The value of the impedance rj varies from 0 for PEC to i® for PMC.
There are many papers devoted to diffraction by impedance boundaries. Impedance boundary conditions (IBC) have been used for the modeling of the scattering properties of good conductors, gratings, etc. In each case there are formulas to define the value of the impedance as a function of material parameters. IBC are approximate BC and therefore they have limitations in usage and cannot describe all diversity of boundaries.
Further approximation of IBC can be made with the aid of derivatives of higher but integer orders or generalized boundary conditions (Hope & Rahmat-Samii, 1995; Senior & Volakis, 1995). A general methodology to obtain exact IBC of higher order in spectral domain is presented in (Hope & Rahmat-Samii, 1995), where flat covers (and also surfaces with curvature) consisting of homogeneous materials with an arbitrary (linear, bi-anisotropic) constitutive equations. It is possible to obtain exact IBC in the spectral domain that can be often done in an analytical form very often. However, it is not always possible to get IBC in the spatial domain in an exact form. That is why it is necessary to approximate IBC in the spectral domain in order to apply inverse Fourier transform.
Another boundary condition that generalizes the perfect boundaries like PEC and PMC was introduced in (Lindell & Sihvola, 2005a). The corresponding surface was named perfect electromagnetic conductor (PEMC) and the mentioned condition is defined as
For M = 0, PEMC defines a PEC boundary and for M = x we get a PMC. The physical model of PEMC boundary was proposed in (Lindell & Sihvola, 2005b) where it was shown that the PEMC condition can simulate reflection from an anisotropic layer for the normal incidence of the plane wave. Diffraction by a PEMC boundary has not been considered yet. Further generalization of PEMC can be made using concept of the generalized soft-and-hard surface (GSHS) (Haninnen et al., 2006):
Fractional boundary conditions (FBC) can be compared with impedance boundary conditions (IBC). First of all FBC are intermediate between PEC and PMC as well as IBC. The value of fractional order a = 0 (a = 1) corresponds to the value of impedance r = 0 (r = i<x>), respectively. For other values of 0 < a < 1 the deeper analysis is needed. Physical analysis of the strip with FBC shows that the induced surface currents behave similarly to the currents on an impedance strip. Due to specific properties the strip with FBC is compared with the well-known impedance strip. It can be shown that for a wide range of input parameters the "fractional strip" behaves similarly to the impedance strip if the fractional order is chosen appropriately (Veliev et al., 2008b). The proposed method used for a "fractional strip" has some advantages over the known methods applied to the analysis of the wave scattering by an impedance strip.
The purpose of this work is to build an effective analytic-numerical method to solve two-dimensional diffraction problems for the boundaries described by fractional boundary conditions with a e [0,1]. The method will be applied to two canonical scattering objects: a strip and a half plane. The method is based on presenting the scattered field via fractional Green’s function,
where
is the unknown function and 
the fractional derivative of the Green’s function defined by equation (2). This presentation leads to the following dual integral equations (DIE) with respect to the Fourier transform
of the function
where dL = a for L = (-a,a), dL = 1 for L = (0,®) .
In the case of a strip resonator, we obtain more complicated set of integral equations which will be presented later in this paper.
The method generalizes the known method used for the PEC and PMC strip and half plane. As will be shown later, this method allows obtaining a solution for the value a = 0.5 in the explicit analytical form. For other values of a e [0,1] the scattering problems are reduced to solving of the infinite systems of linear algebraic equations (SLAE). In order to discretize the DIE the function f 1-a( x) is represented as a series in terms of orthogonal polynomials: Gegenbauer polynomials for the strip and Laguerre polynomials for the half-plane. These representations result in a special kind of the edge conditions for the fractional current density function f 1-a(x). The physical characteristics of the considered scattering objects can be found with any desired accuracy by solving SLAE.
Diffraction by a strip with fractional boundary conditions
Assume that an E-polarized plane wave is characterized with the function
The total field conditions 
must satisfy fractional boundary conditions
is applied with where L = (-a, a) for a strip. For convenience, fractional derivative 
is applied with respect to a dimensionless variable ky . The function Ez (x, y) denotes the z-component of the total electric field Ez (x, y) = Elz + Esz that is the sum of the incident plane wave E’z (x, y) and the scattered field Esz (x, y). Solution to the diffraction by the screen S = {(x, y): y = 0, -a < x < a} is to be sought under the following conditions: – The total field E must satisfy the Helmholtz equation everywhere outside the screen
must satisfy Sommerfeld radiation condition at the infinity
- The scattered field
- The scattered field
must satisfy Sommerfeld radiation condition at the infinity
- The total field E must satisfy the edge condition, i.e. the finiteness of energy in every local area near the edges of the screen (Honl et al., 1961).
- The total field Ez( x, y) must satisfy the boundary conditions (3).
The method is based on representation of the scattered field with the aid of the fractional derivative of the Green’s function:
In (6), the function f 1-a(x) is the unknown function called the density of the fractional potential, and Ga is the fractional derivative of two-dimensional the Green’s function of the free space defined by equation (2).
For the limit cases of the fractional order with a = 0 and a = 1 representation (6) corresponds to the single-layer and double-layer potentials commonly used to present the scattered fields in diffraction problems:
More general representations (6) can be derived from the fractional Green’s theorem (Veliev & Engheta, 2003) which generalizes the ordinary Green’s theorem.
Fractional Green’s theorem
Consider a function y/(r), which satisfies inhomogeneous scalar Helmholtz equation with the source density given by the function p(r):
Besides, define G(r, r0) as the Green’s function of the Helmholtz equation:
Here, 
is the three-dimensional Dirac delta function, r and r0 are the position vectors for the observation and source points, respectively,
Laplacian, and k is a scalar constant. After applying fractional derivatives to equations (7) and (8) with respect to the x variable, multiplying the first equation with 
and the second with 
subtracting one from another, integrating this over all source coordinates x0, y0, z0 inside S, and finally using the Green’s theorem, we obtain the following representation:
where /u + v = P . Operator V0 denotes the operator of gradient in respect of variable r0(x0, y0, z0) . Here it was used the property of the fractional derivative of the Dirac delta function:
We use the uniform symbol
to denote both fractional derivatives and fractional integrals, and it defines a fractional derivative for 0 < a < 1 and a fractional integral for a < 0.
Equation (9) is a generalization of well-known Green’s theorem for the case of fractional derivatives.
Consider some important particular cases, which can be obtained from (9).
In the case of excitation in a free space so that the volume V is the whole space, the surface integrals in (9) vanish, and we have:
Originally function y/(r) characterizes the field excited by the source with the volume density p(r). From the other hand, for P = 0 representation (11) means that the field y/(r) is expressed through the distribution of fractional sources with density D-vp(r0) inside the volume V and by using fractional integral of conventional Green’s function DvG(r0,r). Assuming p(r) = 0, we can obtain some other important representations:
From this representation we see that the fractional derivative of function y/(r) is expressed either via the value of the function and its first derivative at the boundary and the fractional derivatives of Green’s function, or by the fractional derivatives of the function at the boundary and the usual Green’s function.
If v = -, i.e. P = 0, we obtain a representation for the function y/(r) itself:
This expression means that the function y/(r) is represented through its fractional derivatives at the boundary and the fractional derivatives of Green’s function. The equation (13) can be useful in scattering problems. If we have boundary conditions for the function y/(r) on the surface S as
then one of the surface integrals in (13) vanishes and we get a simple presentation for y/(r). This fact will be used to present the scattered field in all diffraction problems considered in this paper (6). Equations (12), (13) generalize the Huygens principle in such a sense that the fractional derivative of the function y/(r), which characterizes a wave process, is presented as a superposition of waves radiated by elementary "fractional" sources distributed on the given surface. "Fractional" potentials,
can be treated as a generalization of well-known single and double layer potentials. 2.2 Solution to integral equations
Substituting the expression (6) for Ez (x, y) into fractional boundary conditions (3) we get the equation
It is convenient to use the Fourier transform of the fractional potential density f1 a (x)
is introduced:
where a new function 
is introduced:
Then the scattered field is expressed via the Fourier transform 
as
where the upper (lower) sign is chosen for y>0 (y<0). Here, in (15), the following representation for the fractional Green’s function was used:
It can be shown that the equation (14) can be reduced to dual integral equations (DIE)
For the limit cases of the fractional order a = 0 and a = 1 the equations (17) are reduced to the well known integral equations used for PEC and PMC strips (Honl et al., 1961; Veliev & Veremey, 1993; Veliev & Shestopalov, 1988; Uflyand, 1977), respectively. In this paper the method to solve DIE (17) is proposed for arbitrary value of a e [0,1].
DIE (17) can be solved analytically for one special case of a = 0.5. In this case we get the solutions for any value of k as
In the case of arbitrary a the solutions can be obtained numerically. First, we modify the equations (17). After multiplying by e-ikaT^ and integrating in £ from -1 to 1, the first equation in (17) can be rewritten in the following form:
In order to discretize this equation, we present the unknown function 
as a uniformly convergent series in terms of the orthogonal polynomials with corresponding weight functions which allow satisfying the edge conditions:
where Ca (x) are the Gegenbauer polynomials and f^ are the unknown coefficients. Gegenbauer polynomials can be treated as intermediate polynomials between Chebyshev polynomials of the first and second kind:
The Fourier transform F1 a(q) is expressed as the series
where Jn+a( kaq) is the Bessel function.
It must be noted that the edge conditions are chosen in the following form
For special cases of a = 0 and a = 1 the edge conditions have the form as
These are well-known Meixner edge conditions in diffraction problems (Honl et al., 1961). Substituting (22) into (17) and taking into account the properties of discontinuous integrals of Weber-Shafheitlin (Bateman & Erdelyi, 1953) and the following formula (Prudnikov et al., 1986)
one can show that the homogenous equation in the set (17) is satisfied identically.
The first equation of (17) written in the form (20) can be reduced to an infinite system of linear algebraic equations (SLAE) with respect to the unknown coefficients f^ :
where the matrix coefficients are expressed as
It can be shown that the SLAE (26) can be reduced to SLAE of the Fredholm type of the second kind (Veliev et al., 2008a). Then the coefficients f^ can be found with any desired accuracy (within the machine precision) using the truncation of SLAE. The fractional density f 1-a(x) is computed by using (21) and the scattered field (6) and other physical characteristics can be obtained as series in terms of the found coefficients f ^ . In order to solve the diffraction problem on a plane screen with fractional boundary conditions and obtain a convenient SLAE we applied several techniques. First of all, the fractional Green’s theorem presented above allowed searching the unknown scattered field as a potential with the fractional Green’s function. The order of the fractional Green’s function is defined from the fractional order of the boundary conditions. In general, the fractional derivative of Green’s function may have a complicated form, but we used the Fourier transform where application of the fractional derivative maps to a simple multiplication by (iq)a . Finally, utilization of the orthogonal Gegenbauer polynomials along with the specific form of the edge conditions allowed to reduce integral equations to SLAE in a convenient form. One can compare the method presented for fractional boundary conditions with the known methods applied to solve diffraction by an impedance strip. The impedance strip requires to consider two unknown densities in presentation of the scattered field as a sum of single- and double-layer potentials. The usage of two unknown functions leads to more complicated SLAE in spite of the SLAE obtained for fractional boundary conditions.
