Electromagnetic-wave Contribution to the Quantum Structure of Matter Part 2

Photon equations of motion

In this section equations of motion for the photon are given and used to calculate a divergence-free Lamb shift [14-15]. As in the case of the electron in Section II we assume that a complex four-potential exists for the photon such that a photon EOM can be written as the Lorentz invariant formed by taking the scalar product of the photon’s four-momentum and the photon’s four-potential,

for either electric or magnetic fields E, H . The photon four-momentum was found in [14] from h times a form of the four-gradient whose scalar product with the four-electromagnetic-energy density gives the electromagnetic continuity equation. This is simply the electromagnetic analog of writing the material continuity equation as the scalar product of the four-gradient and the material four-density.

The electron scalar and vector potentials can be written in the form of carrier-wave expansions,

from which on substituting Eqs. (14) into Eq. (13) and separately setting the coefficients of the exponential factors equal to zero, we obtain,

 

On setting

the photon EOM presented previously assuming zero photon mass

in Eqs. (16) we derive stationary equations

in Eqs. (16) we derive stationary equations for i//E h and %E H; then we eliminate the equation for %E H in favor of a second-order equation for i//E H ,obtaining equations for the electric and magnetic photon wave functions which have the Helmholtz form,

.Eq. (17b) for hmv = 0 was where we have used the identity,

used in previous work to calculate the Lamb shift [14] and anomalous magnetic moment [16].

Subatomic bound states

Dirac’s time-domain equation can be cast in the form of an equationsecond order in space and time; thus we should expect a second spatial-temporal solution to exist which is independent of the first spatial-temporal solution which we have elucidated in Section IV. I show that a regime exists in which an adiabatic solution to the time-dependent Dirac equation is not justified even in an approximate sense. The existence of the regime is easily recognized by writing Dirac equations in the form given by Eq. (11) for the large component with a reversal of charge and for the small component with no reversal of charge and then seeking solutions for which the phase in the exponential factor vanishes for all times. These equations are,

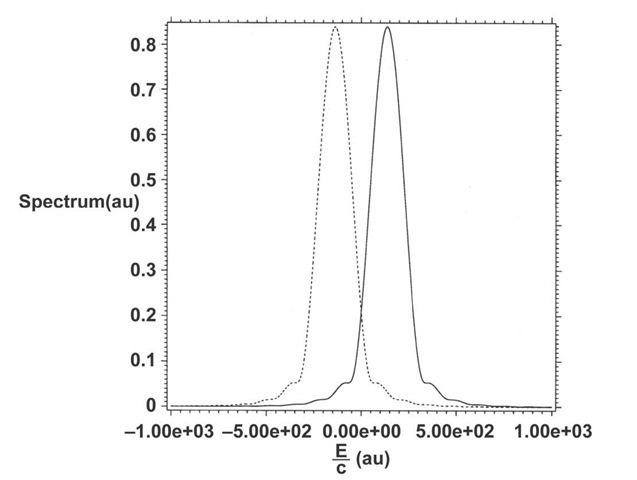
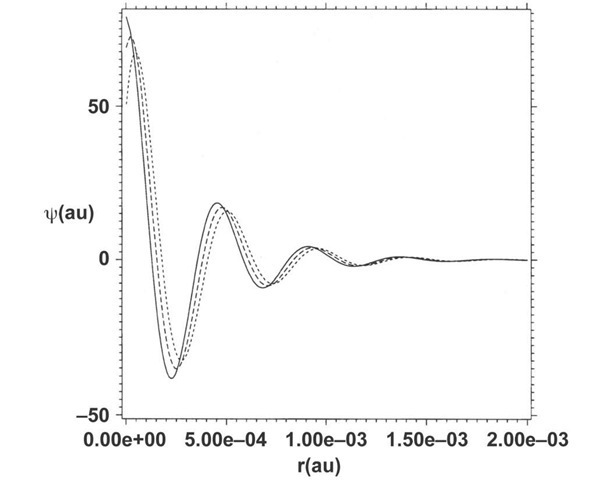
Eqs. (21) are solved numerically for Z=1 and k = ±1 using the same techniques used to solve Eq. (11). The two equations for positronic or electronic binding are solved for a wave function or its complex conjugate respectively. The spectrum is found to be given simply by E± = ±mc2 (Fig. 3). The real part of the wave function is shown in Fig. 4. Notice that if a bound state exists for one charge, then a bound state must also exist for the other charge by the charge-conjugation symmetry of Dirac’s equation. Charge-conjugation symmetry is well known in standard time-independent Dirac theory, whose adiabatic regime does not support positronic-electronic bound states, and arises in Dirac’s interpretation of the negative-energy states in which a hole or absence of an electron registers the existence of a positron or conversely in a positron world the absence of a positron would signal the existence of an electron.

Although the wave function is pulled inward toward the origin, its extent is still large compared to the radius of the proton rp=1.3×10-13 cm = 2.46×10-5 au.

The spectral energies are those which cancel the terms +mc2 on the left side of Eqs. (21) and for which the stationary phases on the right side occur at 2mc2- | V | = 0. For the unit-strength Coulomb potential the radius at which the stationary-phases occur is given by

which is roughly the radius of the proton.

The bound behavior of the positronic-electronic wave function shown in Fig. 4 can be understood as follows. Recognizing that the first and third terms on the left side of Eq. (21) cancel from the spectral values E± = ±mc2 (Fig. 3), one may write an equation in which zero phase of the integration factor is assumed and which is the time derivative of both sides of Eq. (21) with zero phase,

 

A solution to Eq. (22) is sought in the form for the complex separation constant

giving the equation for g,

Fig. 3. Spectra from the solution of Eq. (21) using rmax=0.1 au. Solid: positive charge. Dashed: negative charge. The continuum edges are at E / c = ±mc au. The energy is obtained by multiplying the graphical numbers by c.

Fig. 4. Real part of the positronic or electronic solution of Eq. (21) times r at ct=0.0375 (solid), 0.0750 (dashed), and 0.1125 (dotted) au showing the convergence to a stationary solution. The initial wave function, which s hydrogenic and spread out in the domain 0.25×10-5<r<0.2 au, is pulled into the origin as shown in the figure.

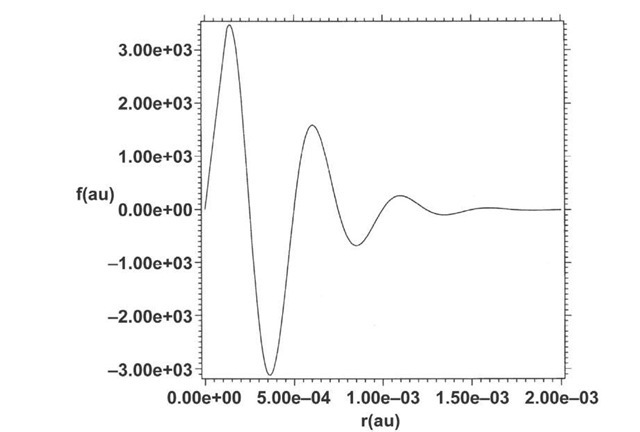
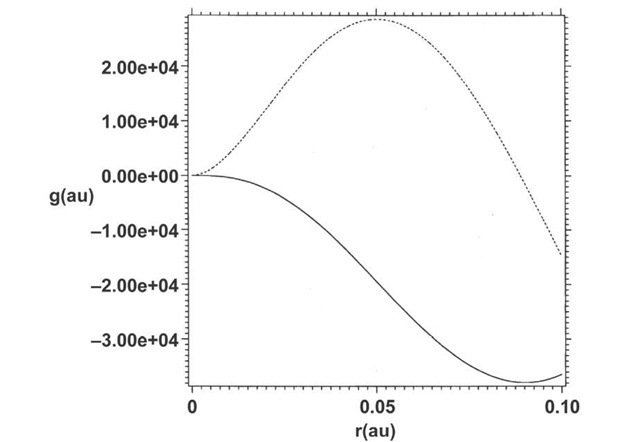
Figs. 5-6 show plots of the real part of f and of the real and imaginary parts of g respectively for r=ct and

Except for the behavior near the origin the unnormalized solution of Eq. (23) is a good mimic of the solution of Eq. (21) shown in Fig. 3. Remarkably the bound positronic-electronic states in the nonadiabatic regime (Fig. 4) exhibit an altogether different form of binding than that of Schroedinger or time-independent Dirac theory. This is obvious from the spectrum (Fig. 3), in which the energies lie at the edges of the positive-and negative-energy continua. One may understand this form of binding as binding which satisfies the four-space Lorentz-invariant relationship rT – (ct)T = 0 between position and time . In other words the binding can occur as a temporal exponential decay in which ct = r rather than as a spatial exponential decay requiring eigenvalues which fall somewhere in the gap between the two continua. This point is clear fromFigs. 5-6 in which binding occurs in the temporal part of the function f(r,t) (Fig. 5) while the radial function g(r) is unbound (Fig. 6).

Fig. 5. Simulation using Eqs. (22)-(23) of the wave function shown in Fig. 4. The simulated wave function is unnormalized. 

Fig. 6. Unnormalized wave function obtained from Eq. (23) by outward integration. Solid: real part. Dashed: imaginary part.