Perspective Two-Frame-Theory for Shape Recovery under Turntable Motion (Computer Vision,Imaging and Computer Graphics) Part 2

Experiments

The proposed method is tested on synthetic models and real image sequence. The camera and light source are fixed and fully calibrated. Circular motion sequences are captured either through simulation or by rotating the object on a turntable for all experiments. Since the derived first order quasi-linear partial differential equation is based on the assumption of small rotation angle, the image sequences are taken at a spacing of at most five degrees.

It has been assumed that the synthetic model has a pure lambertian surface since the algorithm is derived according to the lambertian surface property. It is also quite important to get good boundary conditions for solving the partial differential equations. As for synthetic experiment, it is easier to generate the image without specularities. However, it is hard to control the image sequence without shadows due to the lighting directions and the geometry of the object. From (9), (10), and (11), it can be noted that the solution of the first order quasi-linear partial differential equation mainly depends on the change of the intensities in the two images. If the projection of the point in the first view is in shadow, the estimation of the image intensity using Taylor expansion in the second view will also be inaccurate. The characteristic curves will go crazy (see Figure 2). In order to avoid the great error caused by shadow effect, the intensity difference for the estimation points should not be larger than a threshold ^^which is obtained through the experiments.

Fig. 2. Shadow effect for shape recovery. Left column: original image for one view used for shape recovery and shadow appears near the left arm of the Venus model. Middle column: characteristic curves without using intensity difference threshold for the solution of partial differential equation. Right column: characteristic curves after using intensity difference threshold for the solution of partial differential equation.

Fig. 3. Reconstruction of the synthetic sphere model with uniform albedo. The rotation angle is 5 degrees. Light direction is [0, 0, —1]T, namely spot light. Camera is set on the negative Z-axis. Left column: two original images. Middle column: characteristic curves for frontal view (top) and the characteristic curves observed in a different view (bottom). Right column: reconstructed surface for front view (top) and the reconstructed surface in a different view (bottom).

Experiment with Synthetic Model

The derived first order quasi-linear partial differential equation is applied to three models, namely the sphere model, cat model, and Venus model. Sthre = 51 is used for all the synthetic experiments to avoid the influence of shadow in the image.

The first simulation is implemented on the sphere model. Since the image of the sphere with uniform albedo does not change its appearance after its rotation around Y-axis (see Figure 3), only one image is used to recover the 3D shape. Any small angle can be used to the proposed equation. Nonetheless, if the sphere has non-uniform albedo, two images will be used for shape recovery. Figure 3 shows the original images, the characteristic curves observed in two different views, and the recovered 3D shape examined in two different views. The sphere model is assumed to have a constant albedo. The reconstruction error is tested by using ||Z – Z||2/||Z||2, where Z denotes the estimated depth for each surface point and W · W 2 denotes the I2 norm. The mean error is 4.63% for the sphere with constant albedo which is competitive to the result in [1].

Fig. 4. Shape recovery for the synthetic cat model. Left column: two images used for reconstruction. Middle column: characteristic curves for the view corresponding to the top image in the left column (top) and the characteristic curves observed in a different view (bottom).Right column: Recovered shape with shadings in two different views.

The second simulation is implemented on a cat model. The image sequence is captured under general lighting direction and with rotation angles at three degrees spacing. Seven images are used to get the boundary condition. Two neighboring images are used for solving the derived quasi-linear partial differential equation. The results are shown in Figure 4. It can be observed that the body of the cat can be recovered except a few errors appeared at the edge.

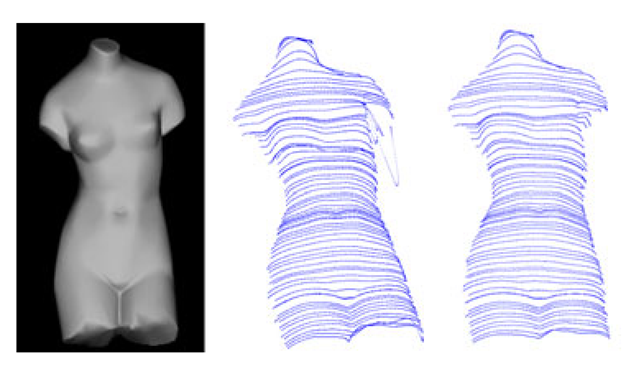
The last simulation is implemented on a Venus model. The sequence is taken at a spacing of five degrees. Similarly seven images are used for getting the boundary condition. The front of the Venus model is recovered by using two neighboring view images for solving the derived quasi-linear partial differential equation. The result is shown in Figure 5.

After the recovery of characteristics curves, shapes for the Cat and Venus model with shadings are shown by using the existing points to mesh software VRmesh. The right columns of Figure 4, and Figure 5 show the results.

Fig. 5. Shape recovery for the Venus model. Left column: two images used for shape recovery. Middle column: characteristic curves for the view corresponding to the top image in the left column (top) and the characteristic curves observed in a different view (bottom).Right column: Recovered shape with shadings in two different views.

Experiment with Real Images

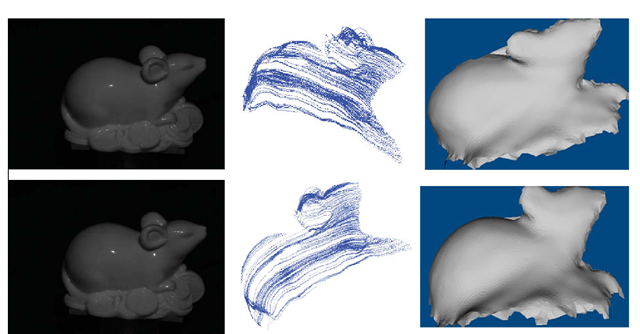
The real experiment is conducted on a ceramic mouse. The mouse toy is put on a turntable. The relative positions of the lighting and the camera is fixed. The image sequence is taken by a Cannon 450D camera with a 34 mm lens. The camera is calibrated using a chessboard pattern and a mirror sphere is used to calibrate the light. The image sequence is captured with the rotation angle at five degree spacing. It can be observed that there are specularities on the body of the mouse. The intensity threshold is used to eliminate the bad effect of the specularities since the proposed algorithm only works well on lambertian surface. In order to avoid the shadow effect for solving the partial differential equation, Sthre = 27 is used which is smaller than the value used in the synthetic experiment since the captured images are comparatively darker. The original images and the characteristic curves are shown in Figure 6. Although the mouse toy has a complex topology and the images have shadows and specularities, good results can be obtained under this simple setting. Right column of Figure 6 shows the results.

Fig. 6. Shape recovery for a mouse toy. Left column: two images used for shape recovery. Middle column: characteristic curves for the view corresponding to the top image in the left column (top) and the characteristic curves observed in a different view (bottom).Right column: Recovered shape with shadings in two different views.

Conclusions

This paper re-examines the fundamental ideas of the Two-Frame-Theory and derives a different form of first order quasi-linear partial differential equation for turntable motion. It extends the Two-Frame-Theory to perspective projection, and derives the Dirichlet boundary condition using dynamic programming. The shape of the object can be recovered by the method of characteristics. Turntable motion is considered in the paper as it is the most common setup for acquiring images around an object. Turntable motion also simplifies the analysis and avoids the difficulty of obtaining the rotation angle in [1]. The newly proposed partial differential equation makes the two frame method more useful for a more general setting. Although the proposed method is promising, it still has some limitations. For instance, the proposed algorithm cannot deal with object rotating with large angles. If the object rotates with large angle, image intensities on the second image cannot be approximated by the two dimensional Taylor expansion. Some coarse-to-fine strategies can be used to derive new equations. In additions, the object is assumed to have a lambertian surface and the lighting is assumed to be a directional light source. The recovered surface can be used as an initialization for shape recovery method using optimization, which can finally get a full 3D model. Further improvement should be made before the method can be applied to an object under general lightings and general motion.