Abstract. Today we know that billions of products carry the 1-D bar codes, and with the increasing availability of camera phones, many applications that take advantage of immediate identification of the barcode are possible. The existing open-source libraries for 1-D barcodes recognition are not able to recognize the codes from images acquired using simple devices without autofocus or macro function. In this article we present an improvement of an existing algorithm for recognizing 1-D barcodes using cameraphones with and without autofocus. The multilayer feedforward neural network based on backpropagation algorithm is used for image restoration in order to improve the selected algorithm. Performances of the proposed algorithm were compared with those obtained from available open-source libraries. The results show that our method makes possible the decoding of barcodes from images captured by mobile phones without autofocus.
Keywords: Barcode recognition, Image restoration, Neural networks.
Introduction
In recent years the growth of the mobile devices market has forced manufacturers to create ever more sophisticated devices. The increasing availability of camera phones, i.e. mobile phones with an integrated digital camera, has paved the way for a new generation of applications, offering to the end users an enhanced level of interactivity unthinkable a few years ago. Many applications become possible, e.g. an instant barcode-based identification of products for the online retrieval of product information. Such applications allow for example, the display of warnings for people with allergies, results of product tests or price comparisons in shopping situations [1]. In Figure 1 an illustration of a typical application that make use of a barcode identification.
There are many different barcode types that exist for many different purposes. We can split these into 1D and 2D barcodes. 1D barcodes are what most people think barcodes are: columns of varying width lines that are imprinted on the back of products. Within the 1D barcode we have EAN-13/UPC-A, Code 128, Code 39, EAN-8 etc. and today we know that billions of products carry EAN-13 bar codes. The two most important parameters influencing recognition accuracy on a mobile camera phone are focus and image resolution, with the former remaining the principal problem; instead low camera resolutions such as 640×480 pixels are not critical [2]. Figure 2 shows an example that highlights the difference between a barcode acquired with a device having autofocus (AF) and without AF. It is evident that images like that in Figure 2(b) present a high level of degradation that makes the decoding process very difficult or even worst, impossible.
Fig. 1. Graphical illustration of the process of a typical application that make use of a barcode identification
Searching the Internet for camera phones with/without AF, we can estimate that about 90% of camera phones is without autofocus1. There are several libraries to decode 1-D barcode but if we analyze the most widespread of these available with an open-source license, all of them show serious difficulties in recognizing barcodes from images captured by devices without autofocus (see some results in Table 1).
Many studies have been made to develop applications for mobile devices capable to decode 1-D barcodes [1,3]. Many studies have aimed to look for efficient and operative algorithms able to recognize a high percentage of codes in a limited time. Others have studied restoration techniques to improve the quality of codes acquired with sensors without autofocus or macro function, and the accuracy of the subsequent decoding [4].
There are several libraries available to decode the multitude of barcode standards. Only a few of these libraries are open-source. One prominent open-source library is the ZXing project2. It has the capability to read not just 1D barcodes but also 2D barcodes. Although this library is widely used and has a great support by the community, it has the common weakness to expect a camera with autofocus and a relatively high resolution in order to work properly. For this reason we decided to work on ZXing library to make it a viable solution when working with devices without autofocus.
In particular, in this work we experiment with a novel restoration technique based on neural networks, in order to improve the quality of the images and therefore the recognition accuracy of 1D barcodes. Image restoration is a process that attempts to reconstruct an image that has been degraded by blur and additive noise[5, 6]. The image restoration is called blind image restoration when the degradation function is unknown. In the present work we perform blind image restoration using a back-propagation neural network and we show how the proposed restoration technique can increase the performance of the selected open-source tool in order to use it with all types of camera phones.
Table 1. Results obtained using some open-source libraries on datasets acquired from devices with and without AF
|
with autofocus |
without autofocus |
|||
|
Sw |
Precision |
Recall |
Precision |
Recall |
|
ZXing |
1.00 |
0.64 |
1.00 |
0.04 |
|
BaToo |
0.95 |
0.58 |
0.60 |
0.13 |
|
JJil |
/ |
0.00 |
/ |
0.00 |
Fig. 2. A sample image captured by a device with autofocus (a) and without autofocus (b)
Identification and Decoding Techniques
The present work focuses on a restoration algorithm to improve the accuracy of a generic 1D barcode decoding process. To make the work self-contained, a brief overview on the state of the art in both image restoration and in decoding barcodes is given here.
Image Restoration
Restoration of an original image from a degraded version is a fundamental early vision task attempting to recover visual information lost during the acquisition process, without introducing any distorting artifacts.
Robust, blind or semi-blind solutions to image restoration are becoming increasingly important as imaging technology is rapidly advancing and finds more applications in which physical and environmental conditions can not be known reliably hampering or precluding estimation of the degrading point spread function (PSF) or the degree and type of noise present.
Regularized image restoration methods [7] attempt to restore an image by minimizing a measure of degradation such as the constrained least-squares error measure.
The critical problem of optimally estimating the regularization parameter has been investigated in depth focusing on the need for adaptive spatially varying assignments.
Within this approach several new methods were developed in recent years, attempting to overcome limits of conventional approaches [8-10]. Artificial neural networks have received considerable attention. Proceeding from early results obtained by Zhou et al. [11] and Paik and Katsaggelos [12], Perry and Guan [5] proposed a method that automatically adapts regularization parameters for each pixel of the image to be restored. The method uses the Hopfield neural model to implement minimization. Neural weights are trained based on local image statistics to take into account image characteristics and to assign each statistically homogeneous area a different regularization parameter value. Other researchers like Guan et al. [13] proposed a network of networks model dividing the image into rectangular images and restoring them with an adaptive restoration parameter. Other techniques render the restoration pixel-wise assigning a separate restoration parameter to each image pixel [14, 15].
Despite the sizable achievement obtained, the diffusion of neural adaptive techniques in operative real world applications is still limited by critical aspects requiring further investigatin. These include high computational cost, difficulties in setting a proper set of internal parameters, and robustness under different levels and types of degradation.
In previous works we defined and experimentally investigated the potential of adaptive neural learning-based techniques for semi-blind image restoration [16-18]. Here, due to the application domain restricted to 1D barcodes, and also bounded by the computational capabilities of mobile phones on which we want to work, we need a simplified version of the models studied in the past.
Barcodes Decoding
Algorithms for decoding barcodes from digital images, can be broken down into two steps: identification and decoding.
An identification algorithm receives in input an image and provides as output the image coordinates that identify the region containing the barcode. There are many different algorithms to perform such operations and in the following we summarize some of them. In [1] the authors presented an algorithm we named Scanline Detection which selects a pixel in the center of the image to be analyzed. Assuming that the pixel belongs to the barcode to be extracted, the algorithm make a horizontal expansion that ends when it finds the ends of the bar code. In [19] the scanline detection algorithm is applied to multiple rows drawn regularly throughout the image. We name Expansion Detection another algorithm presented in [20] that performs vertical and horizontal expansion starting from the center pixel of the image to be analyzed. Other two interesting algorithms are those presented in [21] and [22] using Hough Transform and Canny Edge Detection respectively.
A barcode decoding algorithm receives in input an image and a sequence of coordinates and returns as output one or more strings containing the values recognized. Unlike identification, the decoding process is standard and is greatly simplified by the redundant structure that every barcode has. Some interesting decoding algorithms are briefly described below. The algorithm proposed by [19, 23] we named Line Decoding, reads a line of barcode and makes the decoding. The algorithm is able to understand if a code has been read correctly by analyzing the control code contained within the barcode. Multi Line Decoding, proposed in [1], is an extension of the Line Decoding algorithm, where the Line Decoding is applied at the same time to a set of parallel image rows. The code will be constructed collecting the digits that appear several times in all the lines analyzed. Finally, a very different approach is based on neural networks trained to recognize the codes. This algorithm, which we called Neural Net Decoding, was presented in [24].
The Proposed Method
The neural restoration algorithm we propose in this paper was added in the ZXing library, a library that was proved robust decoding of 1D barcodes.
ZXing uses a modified version of the algorithm proposed by [19] and mentioned in the previous section. The changes allow ZXing to identify 1D barcodes placed in a non-horizontal position, partially missing and placed in non-central position within the image portion. The ZXing’s identification and decoding process is summarized in Algorithm I. A special parameter try Jiarder can be enabled to increase the number of lines considered in the process and the number of rotations of the input image, to search barcodes placed in a non-horizontal position. This latest process is done by rotating the image and re-applying the Algorithm 1 until the code is not identified.
The decoding is based on the Line Decoding algorithm described in the previous section.
Algorithm 1. The ZXing’s identification and decoding process
The barcode decoding process requires the image containing the code to be binarized. The image binarization is usually carried out using a thresholding algorithm. However there is an high chance that the image involved in the process is blurred and/or noisy, making the thresholding phase non-trivial. All the software tested in this work show their limits when faced with such images, with a high failure rate in the decoding process. The main contribution of this work is the definition and evaluation of a restoration technique that, complemented with an adaptive thresholding, can be proposed as an alternative to standard binarization. We base our strategy on the Multilayer Perceptron model trained with Backpropagation Momentum algorithm. The netwok has five input neurons, five output neurons and three hidden layers with two neurons in each layer. This configuration was chosen as it provides a high-speed in generalization combined with a high accuracy.
Fig. 3. An example of training image captured by a device without autofocus (a), and its expected truth image (b). Only the rectangular section containing the barcode was extracted from the original image.
The network can learn how to restore degraded barcodes if trained with a proper amount of examples of the real system to be modeled. An example of degraded input image and its desired output is illustrated in Figure 3. The truth image (or output image) was created using a free online service to generate barcodes3 and aligned to the input image using a computer vision algorithm called Scale-Invariant Feature Transform (SIFT) [26]4.
Training samples are presented to the neural network having the following form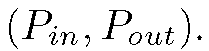 
The input pattern
is a sequence of S values, one for each input neuron, where
is the ith pixel of the row Ly scaled in [0,1].
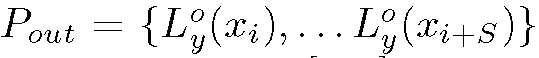is the expected output extracted from the truth image and then scaled in [0,1], at the same position of the Pin pattern. Given a pair of training images having width W, we select only one line Ly and a number of patterns equal to W – S +1, moving the input window p = 1 pixels forward for each new pattern. The training and test set creation was performed using degraded input images acquired by 1MP camera without autofocus at variable distances.
The trained neural network performs the restoration for never seen input patterns Pin transforming the input pixel values to gray levels without blur and noise. The algorithm is applied on each single line Ly selected by the identification algorithm. During the restoration phase, according to the step value p and size S of the input window, each pixel can be classified more than once. A decision rule must be accomplished to compute the final value of the restored image. In the present work for each pixel
the value of average output activation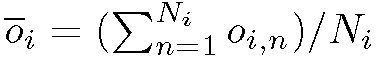
is calculated, where Ni is the number of times in which the pixel has been classified by the neural model and Oi is the activation of the ith output neuron. Binarization process adopted for the restored images simply evaluate the average activation value Oi and sets a threshold at 0.5.
We named ZXing-MOD the library ZXing with the addition of our neural restoration process. The new algorithm is very similar to the original described in Algorithm 1, only the lines 5 and 6 have been replaced respectively by the neural restoration process and the binarization technique described above. The number of lines to be analyzed and decoded is deduced from a parameter called rowStep.
