Clipping (Basic Computer Graphics) Part 4

Maillot Polygon Clipping

The Maillot clipping algorithm ([Mail92]) clips arbitrary polygons against a rectangular window. It uses the well-known Cohen-Sutherland clipping algorithm for segments as its basis and then finds the correct turning points for the clipped polygon by maintaining an additional bit of information. As indicated earlier, it is speedy determination of turning points that is crucial for polygon clipping, and this algorithm does it very efficiently. We shall use the same notation that was used in Section 3.2.1. We also assume that the same encoding of points is used. This is very important; otherwise, the tables Tcc and Cra below must be changed.

Let P be a polygon defined by the sequence of vertices Algorithm 3.3.4.1 gives a top-level description of the Maillot algorithm.

In addition to the Cohen-Sutherland trivial rejection cases, Maillot’s algorithm subjects all vertices of the polygon to one extra test, which he calls the “basic turning point test.” This test checks for the case where the current point lies in one of the four corners outside the window.

Algorithm 3.3.4.1. Overview of Maillot polygon-clipping algorithm.

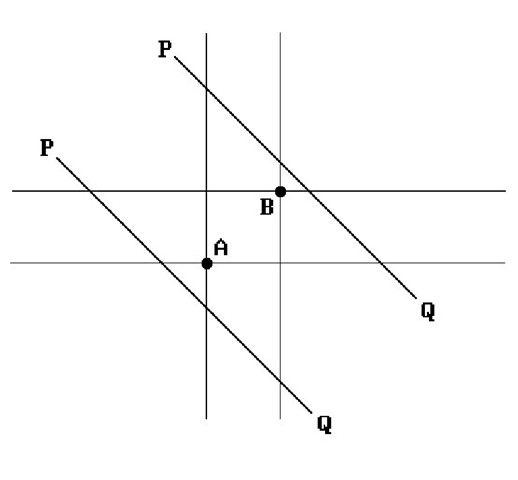
Figure 3.14. A turning point case.

One probably needs to add a turning point to the clipped polygon in this case. See Figure 3.14. We said “probably” because if the current point is considered in isolation (without looking at its predecessors), then to always automatically add the point may cause us to add the same corner several times in a row. See points pi, pi+1, and pi+2 in Figure 3.14. In the implementation of Maillot’s algorithm, we do not try to eliminate such redundancies. If this is not desired, then extra code will have to be added to avoid it.

If all of a polygon’s edges meet the window, then the basic turning point test is all that is needed to clip it correctly. For polygons that have edges entirely outside the clipping region, one needs to do more. Figure 3.15 shows all (up to symmetry) generic cases that need to be handled in this more complex situation. The following terminology is useful for the case of edges outside the clipping region.

Notation. A point that lies in a region with code 0001, 0010, 0100, or 1000 will be called a 1-bit point. A point that lies in a region with code 0011, 0110, 1100, or 1001 will be called a 2-bit point. A segment is called an x-y segment if its start point is an x-bit point and its endpoint is a y-bit point.

Knowing the type of segment that one has is important for the algorithm. This is why an extra bit is used in the encoding of points. It is stuck at the left end of the original Cohen-Sutherland code. Below is an overview of the actions that are taken in the TestForComplexCase procedure. Refer to Figure 3.15.

The 1-1 Segment Cases (Segments a and b). Either the two points have the same code (segment a) and no turning point needs to be generated or they have different codes (segment b). In the latter case there is one turning point that can be handled by the basic turning point test. The code for the corner for this turning point is computed from the or of the two codes and a lookup table (the Tcc table in the code).

The 2-1 and 1-2 Segment Cases (Segments c and d). In this case one point of the segment has a 1-bit code and the other, a 2-bit code.

(a) The endpoint is the point with the 1-bit code (segment c): If both codes and to a nonzero value (segment [P,R] in Figure 3.16(a)), there is no turning point. If both codes and to zero, then we need to generate a turning point that depends on the two codes. A lookup table (Tcc in the code) is used for this.

Figure 3.15. Turning point cases in Maillot algorithm.

Figure 3.16. Turning point tests.

(b) The endpoint has the 2-bit code (segment d): The case where the and of both codes is nonzero is handled by the basic turning point test (segment [R,Q] in Figure 3.16(b). If both codes and to zero, we need two turning points. The first one depends on the two codes and is determined by again using a lookup table (Tcc in the code). The other is generated by the basic turning point test (segment [P,Q] in Figure 3.16(b)).

As an example of how the Tcc table is generated, consider the segment [P,Q] in Figure 3.16(b). In the figure there are two turning points A and B. The basic turning point test applied to Q will generate B. Let us see how A is generated. How can one compute the code, namely 3, for this turning point? Maillot defines the sixteen element Tcc table in such a way that the following formula works:

For the 1-1, 2-1, and 1-2 segment cases only four entries of Tcc are used in conjunction with this formula. Four other entries are set to 1 and used in the 2-2 segment case discussed below when it runs into a 1-1 segment. The remaining eight of the entries in Tcc are set to 0.

The 2-2 Segment Case (Segments e, f and g). There are three subcases.

(a) Both points have the same code (segment e): No turning point is needed here.

(b) Both codes and to a nonzero value (segment f): Apply the basic turning point test to the end point.

(c) Both codes and to a zero value (segment g): There will be two turning points. One of them is easily generated by the basic turning point test. For the other one we have a situation as shown in Figure 3.17 and we must decide between the two possible choices A or B. Maillot uses a midpoint subdivision approach wherein the edge is successively divided into two until it can be handled by the previous cases. The number of subdivisions required depends on the precision used. For 32-bit integers, there will be less than 32 subdivisions.

Figure 3.17. 2-2 segment  case turning points. 

Maillot presents a C implementation of his algorithm in [Mail92]. Our version of this algorithm is Algorithm 3.3.4.2 below. The main difference is that we tried to be as clear as possible by using extra auxiliary functions and procedures. To be efficient, however, all these calls should be eliminated and the code put inline.

As mentioned earlier, Maillot’s algorithm uses the Cohen-Sutherland clipping algorithm. One can use the implementation in Section 3.2.1 for this except that the extended encoding function (ExtendedCsCode) shown in Algorithm 3.3.4.3 should be used. This function adds the extra bit (TWOBITS), which we talked about. Within the Cohen-Sutherland clipping the extra bit should be ignored.

Algorithm 3.3.4.2. The Maillot polygon-clipping algorithm.

Algorithm 3.3.4.2. The Maillot polygon-clipping algorithm.

Algorithm 3.3.4.2. The Maillot polygon-clipping algorithm.

Algorithm 3.3.4.2. The Maillot polygon-clipping algorithm.

Algorithm 3.3.4.3. An extended clipping code function.

Two functions in the Maillot algorithm, Algorithm 3.3.4.2, make use of Cohen-Sutherland clipping:

SEGM means that the segment is inside the clipping region

CLIP means that the segment is only partly inside the clipping region

NOSEGM means that the segment is outside the clipping region

In conclusion, Maillot claims the following for his algorithm and implementation:

(1) It is up to eight times faster than the Sutherland-Hodgman algorithm and up to three times faster than the Liang-Barsky algorithm.

(2) It can be implemented using only integer arithmetic.

(3) It would be easy to modify so as to reduce the number of degenerate edges.

With regard to point (3), recall again that the Sutherland-Hodgman and Liang-Barsky algorithms also produce degenerate edges sometimes. The Weiler and Vatti algorithm are best in this respect.