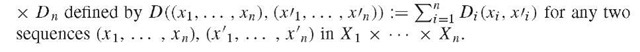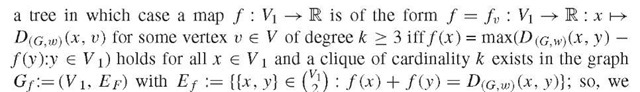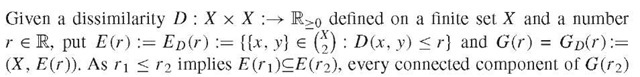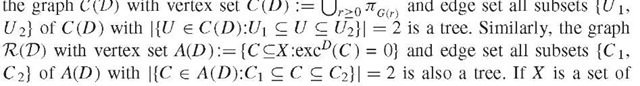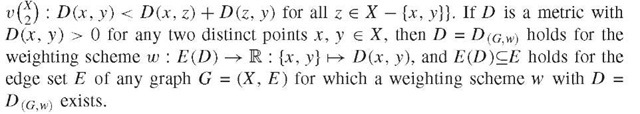1. Generalities
Graphs and metrics are structures that allow to specify and represent mutual relationship between pairs of objects from a given collection of objects under consideration. The most abstract form of representation consists in just a list specifying all pairs of objects that are considered to be “related” (relative to some preconceived concept of relatedness). Additional information regarding a “quantifiable degree of relatedness” can be specified by providing, in general for every pair x, y of objects, a nonnegative real number S (x, y) measuring their similarity – or, conversely, a number D(x, y) measuring their dissimilarity (or distance).
2. Basic definitions
1. In consequence, one defines a (simple undirected) graph G to be a pair (V, E) consisting of a set V = VG called the vertex set of G (representing the objects) and a subset E = EG of the set (2) of 2-subsets of V called its edge set. The degree dG(v) of a vertex v e V is the number of elements in its G-neighborhood NG(v) :={u e V : {v, u} e E}. If V is a finite set of cardinality | V|=: n = n(G) – in which case G is called a finite graph – one has 0 < dG(v) < n for every ^V,
(which, by the way, implies that every finite graph contains at least two vertices of the same degree because n < 1 for all i = 0, 1,… ,n – 1 would imply ni = 1 for all i = 0, 1,… ,n — 1, while ni = 0 holds for all i > n — (n0 + 1)). A
u is a sequence v0, vi,… , ve of t + 1 vertices on V with v0 = v,vt = u, and {v0, v1}, {v1, v2},… , {vt-1, vt} e E. A connected component of G is a minimal nonempty subset C of V such that u e C holds for every u e V for which a G -path from u to some vertex v e C exists (or, equivalently, a maximal subset C of V such that a G-path from u to v exists for any two vertices u, v e G). The vertex sets of the connected components of G form a partition of V , denoted by nG. G is connected if \nG\ = 1 (or, equivalently, nG = {V}) holds. A G-cycle is a path x0, x 1, … ,xn with xn = x0 and \{x1;… , xn}\ = n> 2. G is called a tree if it is connected and does not contain any G-cycle. One has \V\ <\E\ + 1 for any finite connected graph G = (V, E), with equality holding iff (=if and by nG. G is connected if \nG\ = 1 (or, equivalently, nG = {V}) holds. A G-cycle is a path x0, x 1, … ,xn with xn = x0 and \{x1;… , xn}\ = n> 2. G is called a tree if it is connected and does not contain any G-cycle. One has \V\ <\E\ + 1 for any finite connected graph G = (V, E), with equality holding iff (=if and
every finite tree with at least two vertices. More generally, the cycle number C1(G); := \E\ + \nG\ — \V\ is a non-negative integer for every finite graph G. For every connected graph G = (V, E), there exists a spanning tree, that is, a tree with vertex set V whose edge set is a subset of E. Every finite tree (V, E) with \ V \ >2 contains at least two leaves, that is, vertices of degree 1, and – in case \ V \ >5 and n2 = O – at least two disjoint cherries, that is, pairs of distinct leaves u, v with NG(u) = NG(v).
2. Given any set X, a map D from X x X := {(x, y ):x, y e X} into the set R U {+c} is called symmetric if D(x, y) = D(y, x), a similarity if D(x, x) > D (x, y), and a dissimilarity if D (x, x) = 0 < D (x, y) holds for all x, y e X .A dissimilarity is called a metric if D (x, y) < D (x, z) + D (y, z) holds for all x, y, z e X. The diameter D(C) of a subset C of X relative to a dissimilarity D is defined by D(C) := sup(D(x, y) : x, y e C). The D-rank rkD (y) of an element y e X relative to some element x e X is defined by rkD(y) := \ {z e X : D(x, z) < D(x, y)} \ and the D-rank of a subset C of X by rkD(C) := max(rkD(y) : x, y e C). One has excD(C) := rkD(C) — \ C\ >0 for every CCX, and | C1 U C2 \ < max (rkD(CO, rkD(C2)) < max( \ C1\,\ C2 \) + max(excD(Ci), excD(C2)) for all Ci, C2cx with C1 n C2 = 0. In particular, one has Ci n C2 = 0, CiCC2, or C2CC1 for all C1, C2C X with excD(C 1) = excD(C2) = 0. Note that rkD1 (y) = rkD2 (y) holds for all x, y e X for any two homologous dissimilarities D1 and D2, that is, with D 1(x, z) < D 1(x, y )^D2(x, z) < D (x, y) for all x, y, z in X.
Given n sets X1, … , Xn with metrics Di : Xi x Xi ^ R>0 (i = 1,…, n), the product space X1 x ••• x Xn consisting of all sequences (x 1, … , xn) with xt e Xi for all i = 1 … , n, is a metric space relative to the metric D :=D1 x
3. From graphs to metrics
D(u, v) < w({u, v} for all u, v e V with {u, v} e E. In case w(e) = 1 holds for all e e E, one also writes DG instead of D (Gw). Clearly, one has (1)
C of V equals 1 iff C is a clique, (3) {u, v}e E for any two elements u, v e V iff DG(u, v) = 1 holds and, provided G is finite, also (4) D(Gw) (x, y) + D(G,w)(u, v) < max(D(G,w)(x, u) + D(G,w)(y, v), D(G,w)(x, v) + D(g,w) (y, u)) for all x, y, u, v e V for some (or all) weighting scheme(s) w iff G is
can recover V (and then also E and w) from the restriction of D (G,w) to V i in case n2 = 0 holds.
4. From metrics to graphs
is a disjoint union of connected components of G(r 1) in this case, implying that
species and D a measure of their genetic dissimilarity , these trees can be viewed as putative phylogenetic trees for X. Of interest is also the graph with vertex set X and edge set E(D) := f\x, y) e
5. An example: graphs in sequence assembly
In whole-shotgun sequencing, sequence assembly can be performed by studying the overlap graph of a given collection of subsequences identified, for example, by PCR procedures: Given a finite set A of “letters”, a string a := a 1a2 … aN of length N, a positive integer k < N, and a collection C of subsequences of length k of the form ai+1ai+2 … ai+k of a, the problem is to reconstruct a from the subsequences in C. While it is obvious that this is not always possible (e.g., the sequences abcabab and ababcab have the same set of subsequences of length 3 -so this is not even necessarily possible if C consists of all subsequences of length k and if all of these are distinct), one can still try to find at least one, or even all, strings a that would be compatible with the given collection C of k-strings. To this end, one can proceed as follows: One considers the associated overlap graph G = G(C) whose vertices are the strings in C and whose edges are the pairs a 1 … ak and b1 … bk of strings in C for which a2 … ak = b1 … k-1 holds (note that these edges come with a preferred direction, that is, that from a 1 … ak to b1 … bk). The task is to find a shortest path in that graph that respects directions and visits every vertex at least once. This is a typical problem in the important area of graph algorithms, which, though unfortunately much too extensive to be covered in this article, still relies strongly on the concepts collected above.
6. Discussion
The above concepts and facts provide a highly flexible framework for dealing with complex data (in particular, discrete data with large degrees of freedom) such as collections of genetically related sequences, interaction patterns of biomolecules, and/or biochip data. Genomics, proteomics, toponomics, and metabolomics all rely on comparative data analysis and, hence, on the analysis of relationships encoded by coincidence or, at least, (dis)similarity. References could easily fill many pages. However, endowed with a solid understanding of the concepts and constructions presented above, most of their applications within these contexts should be sufficiently transparent or, at least, accessible.