27.4.
The Ackermann Principle as Applied to Steering
27.4.1.
The Ackermann Principle
To achieve true rolling for a four wheeled vehicle moving on a curved track, the lines drawn through each of the four wheel axes must intersect at the instantaneous centre (Fig. 27.23). The actual position the instantaneous centre constantly changes due to the alternation of the front wheel angular positions to correct the steered vehicle’s path. Since both rear wheels are fixed on the same axis but the front wheel axles are independent of each other , the instantaneous centres lies somewhere along an imaginary extended line drawn through the axis of the rear axle.
The Ackermann principle is based on the two front steered wheels being pivoted at the ends of an axle-beam. The original Ackermann linkage has parallel set track-rod-arms, so that both steered wheels swivel at equal angles. Consequently, the intersecting projection lines do not meet at one point (Fig. 27.24.). If both front wheels are free to follow their own natural paths, they would converge and eventually cross each other. Since the vehicle moves along a single mean path, both wheel tracks conflict continuously with each other causing tyre slip and tread scrub. Subsequent modified linkage uses inclined track-rod arms so that the inner wheel swivels about its king-pin slightly more than the outer wheel. Hence the lines drawn through the stub-axles converge at a single point somewhere along the rear-axle projection (Fig. 27.25).

Fig. 27.24. Side-pivot steering with parallel-set track-rod arms.

Fig. 27.25. Side-pivot steering with inclined track-rod arms.
27.4.2.
Ackermann Linkage
The self propelled motor vehicle almost from the beginning, used the double pivot wheel steering system. This was invented for horse drawn vehicles in 1817 by George Lankensperger, a Munich carriage builder. In England, Rudolph Ackermann acted as Lankensperger’s agent and a patent of the double-pivot steering arrangement was taken in his name.
With this layout of the linkage the track rod arms are set parallel to each other and a track rod joins them together. In the straight ahead position of the steering, the linkage and axle beam forms a rectangle, but, as the stub-axles are rotated about their king pins, the steering arrangement forms a parallelogram. This linkage configuration turns both wheels the same amount. Figure 27.26A illustrates the parallel-set linkage positioned to provide both a 20 degrees and a 40 degrees turn for the inner and outer wheels.
Charles Jeantand in 1878 introduced an improvement to the Ackermann linkage layout in which inclined track rod arms form trapezium (Fig. 27.25). This trapezium linkage configuration allows the inner wheel to rotate about its king-pin pivot by a greater amount than the outer wheel, which is necessary for providing semi-true-rolling (Fig. 27.26B and C). True rolling is obtained in the straight ahead position and on the left and right hand turns (locks). In between these three positions, only partial true rolling occurs. The degree of departure from true rolling and hence the amount of tyre scrub occurrence depends mainly on the ratio of track-rod to track-rod-arm lengths, and on the track-rod-arm angular inclination or set. In case the steering linkage dimensions and settings are carefully selected, a very little misalignment takes place for angle of turn up to about 15 degrees, beyond which the error increases rapidly. Also the deviation of the linkage from the theoretical true-rolling angles can readily be corrected by the tyre’s side-wall flexibility and tread distortion, provided the angular error between the steered wheels is small. Since the rear wheels turn on a smaller radius than the front wheels, it is easier to manoeuvre a vehicle in reverse than in the forward direction when parking.
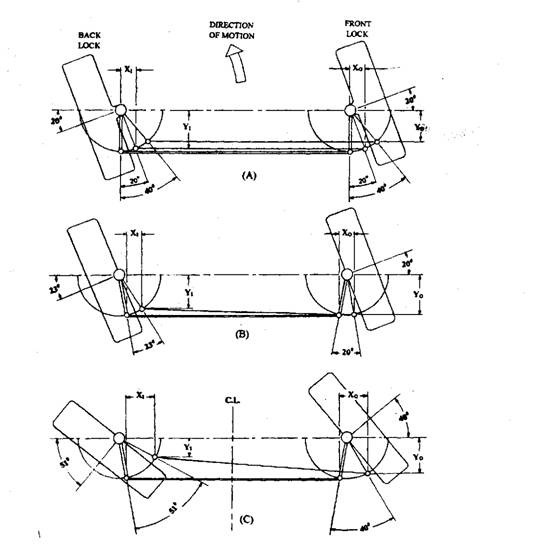
Fig. 27.26. Ackermann linkage geometry.
A. Parallel set track-rod arms, outer wheel turned 20 and 40 degrees.
B. 10 degrees set track-rod arms, outer wheel turned 20 degrees.
C. 10 degrees set track-rod arms, outer wheel turned 40 degrees.
27.4.3.
Ackermann-linkage Geometry
In parallel-set steering arms layout (Fig. 27.26A), the track-rod dimensions yi, xi andy0, x0, remain equal for all angles of turn. With the inclined arms (Fig. 27.26B and C), the inner-wheel track-rod end dimension yi, is always smaller than the outer wheel dimension y0, while negotiating a curve. On the other hand, there is very little variation between xi and x0 for small angular movements. For small steering angles about the king-pin up to say 10 degrees, there is very little difference between yi and y0 and between the inner and outer wheel turning angles.
Figure 27.26B illustrates that for a 10 degrees set track rod arms if the outer wheel is turned at 20 degrees, then the corresponding inner wheel is shown to rotate 23 degrees. Similarly for the same set, for 40 degrees outer wheel turn, the inner wheel rotates 51 degrees (Fig. 27.26 C). Therefore, for a given angular movement of the stub axles, the inner-wheel track-rod arm and track-rod are more effective than the outer-wheel linkage in turning the steered wheel. For a given amount of transverse track-rod movement with inclined track-rod arms, the least effective angular displacement of stub-axle pivot occurs in the straight-ahead region, and the most effective angular displacement takes place as the stub-axles move away from the mid-position. Thus, the angular movement of the inner wheel relative to the outer wheel becomes much greater as both wheels approach movement of the inner wheel relative to the outer wheel becomes much greater as both wheels full lock (Fig. 27.27). With modern radial tyres, the difference between front and back-lock steering angles is sometimes reduced.
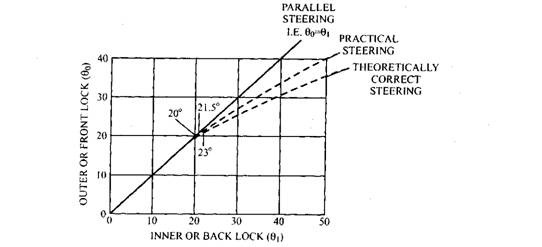
Fig. 27.27. Front and back lock steering-angle curves.
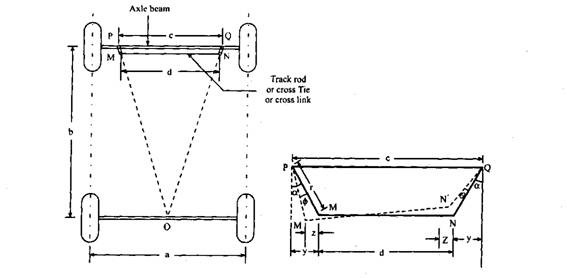
Fig. 27.28. Analytical solution diagram for Ackermann-linkage.
Analytical Solution.
If the slight inclination of the track rod (Fig. 27.28) is neglected, the movements of M and N in the direction parallel to the axle beam PQ can be considered as the same, say z. Let M’, N’ represent the correct steering position and, r, denote the cross-arm radius.
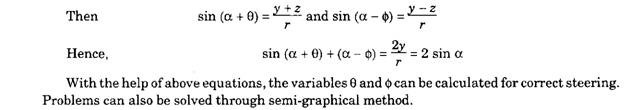
Example 27.2. A track has pivot pins 1.37 m apart, the length of each track arm is 0.18 m and the track rod is behind front axle and 1.27 m long. Determine the wheel base which will give true rolling for all wheels when the car is turning so that the inner wheel stub axle is 60° to the centre line of the car. A geometrical construction may be used.

Example 27.3. The distance between the king-pins of a car is 1.3 m. The track arms are 0.1525 m long and the length of the track rod is 1.2 m. For a track of 1.42 m and a wheel base of 2.85 m, find the radius of curvature of the path followed by the near-side front wheel at which correct steering is obtained when the car is turning to the right.
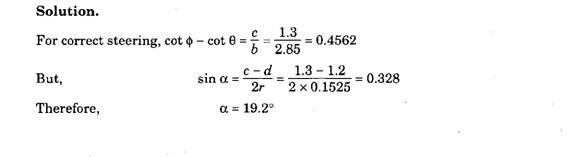


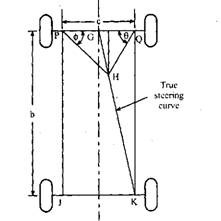
Fig. 27.30. Graphical solution diagram for Ackermann-linkage.
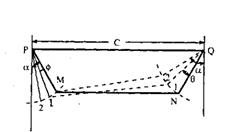
Fig. 27.31. Deflection of outer wheels for assumed deflection of inner wheel.
Thus for the graphical representation of the steering mechanism on a paper of reasonable size with a sufficient degree of accuracy, it can be assumed that the steering arms are of definite length and make a certain angle with the longitudinal axis of the vehicle.
Now determine graphically the deflection on the outer wheel, <|> for various assumed deflection of the inner wheels, say 0 = 10°, 15°, 20°, 25°, 30°, 35°, 40° and 45° for these steering arms as shown in Fig. 27.31.
After knowing these values of 0, the corresponding angles 9 and $ are laid off on the opposite ends of the line C as shown in Fig. 27.32. A curve is then drawn through the intersection of lines describing the angle 9 and <j) correspondingly. The curve drawn is called steering error curve, because their deviation from true steering curve indicates the error in the steering angles. The angles 9 and § corresponding to the intersection of these two curves determine the correct steering angle for a particular a and c/b. If a is changed for the same c/b another steering error curve is obtained. Thus it can be concluded that the
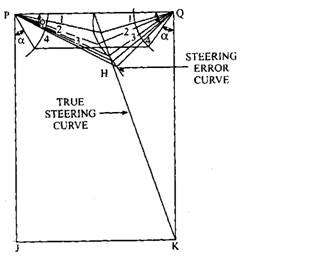
Fig. 27.32. Steering error curve.
most advantageous angle of the knuckle arms, i.e. a depends upon the turning range of the inner wheel.
