The Application of FSP Models in Automatic Optimization of Software Deployment (Software and Computer Systems) (Analytical and Stochastic Modeling) Part 2

Implementation

We have implemented the deployment algorithm discussed in the previous section using a multi-point hill climbing algorithm. In a multi-point hill-climbing algorithm, a set of arbitrary solutions in the search space are selected as the starting points of the hill-climbing search. By starting from each solution, the algorithm attempts to find a better solution by incrementally changing a single element of the solution. If the change produces a better solution it is accepted as the new solution. For each solution si, all the solutions like sk which can be produced by changing a single element of si, are called neighbors of si within the search space. This procedure is repeated until no further improvements can be found. Assuming that by starting from an initial solution si a (near)optimal solution pi is achieved, the best solution among p1..,pn is picked as the optimal solution. In this approach since more than one path is tried, the larger portion of the search space will be examined. The objective of the hill-climbing algorithm is to find a deployment d (which is a solution in the search space) for which the lowest response time is resulted. The response time corresponding to each deployment d is computed according to relation (5). Within the search space, each object deployment d is represented by a solution string. The ith place in string p holds the machine number on which the ith object is deployed. Assume that we want to find the optimal deployment of six objects: o1.o6 , belonging to use-case u, over four machines m1..m4. Each possible deployment of these objects is represented by a string of six numbers each in the range of 1 to 4. A sample deployment and its corresponding string are presented in Figure 4. The hill Climbing algorithm starts with a population of randomly generated strings D={dbd2,d3…,d k}. For each string di in the population, the algorithm repeatedly finds a neighbor solution dk, such that 0s(dk) is less than 0s(di). Each neighbor of solution di is produced by replacing one of the machine identifiers in di string with another machine identifier. In Figure 4 an object deployment corresponding to solution string 1,1,1,2,3,4 and three neighbors of this solution are shown. As explained earlier, the input to our deployment algorithm is an XML file containing: (1) Scenario Call Flow Graph: The flow of method calls among objects within a scenario. For each invocation Ii in the scenario, the set of all blocking and non-blocking calls within Ii, the synchronization point of Ii and the set of all concurrent invocations with Ii are also kept. (2) Scenario execution Loads and (3) Resource Capacities.

Case Study: An Accounting Web Application

This is a real world web application used in ISP companies by which a customer can purchase an account for accessing Internet. The main success scenario of the Purchase-Account use-case is as follows:

Fig. 4. A deployment of six objects over four machines

(1) The customer navigates to the purchase page. (2) The system shows available Internet packages. (3) The customer selects a package and confirms. (4) The system navigates to the bank payment page. (5) The customer pays the package price. (6) The system verifies the payment and creates an account in AAA software and submits the created account to the customer.

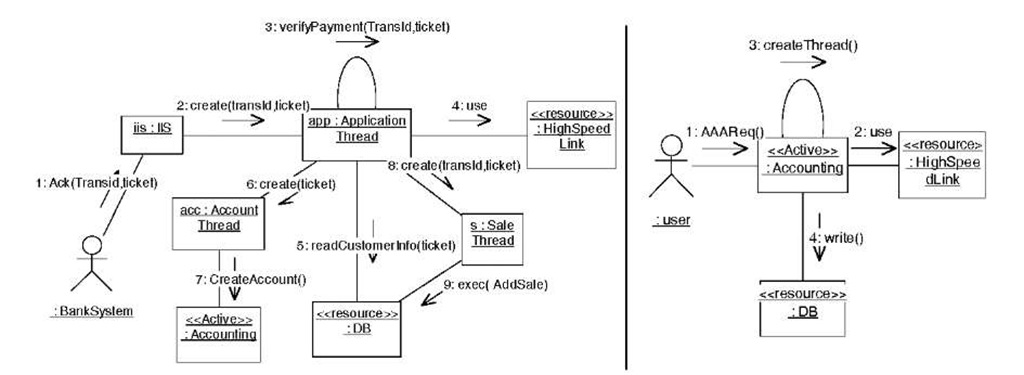
In this case study, not only the purchase-account requests to the web application is often high, but also the AAA software is very busy due to processing of many authentication requests from different Access Points inside the company network. Our observation showed that without correct deployment of this software over the available resources, many purchase requests to the application fails at step (6) (of the above scenario) due to the overloaded web application. Therefore it is essential to find the optimal deployment for this software over the available computing resources of the company in order to achieve the best performance. In Table 2, the characteristics of computing nodes and their associated resources are presented. The communication diagrams corresponding to the purchase-account and Authenticate use-cases are shown in Figure 5. Note that objects with <<resource>> stereo-type represent system resources and have fixed location as listed in Table 2.

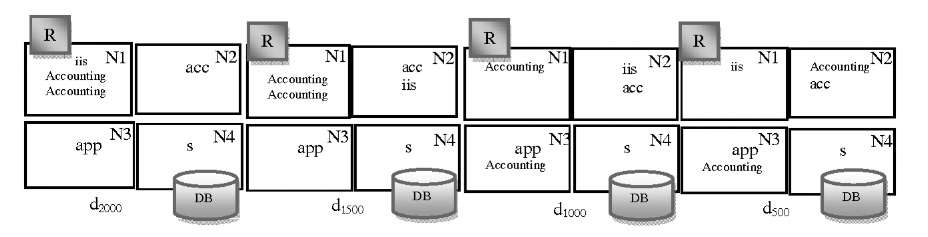
We simulated both scenarios as a single concurrent system using LTSA to measure the required metrics(Uo, Po, RTi). The Purchase-Account scenario was simulated with an exponentially distributed input workload with four mean values: 500ms, 1000ms, 1500ms and 2000ms (which are the interval between requests). The input workload for the simulation of Authenticate scenario was also chosen exponentially with mean values: 200ms. Our deployment algorithm found the following deployments corresponding to each input workload(see Figure 6).

Table 2. The computing nodes and their associated resources

Note that the objective function of the deployment algorithm was to find deployment d for which the value [0s(d)+ 0s'(d)]/2 is minimal where s and s’ are the scenarios corresponding to the Purchase-Account and Authenticate use-cases.

Fig. 5. Purchase-Account scenario (left), Authenticate scenario (right)

Fig. 6. The near-optimal deployments corresponding to workloads 2000,1500,1000 and 500 (R denotes Router)

Discussion

As explained before, for each input workload x to the system a set of simulation data were obtained and subsequently fed into our hill-climbing algorithm to find the near-optimal deployment dx corresponding to workload x for the intended case-study. It is observed that changes to the input workload resulted in changes to the optimal deployment. For example consider two deployments d2000,d 1500 in Figure 6. Recall that both iis and Accounting objects need the high-speed-link R associated with N1. For input workload 2000(low load) iis and Accounting objects are assigned to N1 to access

R locally (to eliminate any communicational delay to access this resource). However, as the input workload to scenario Purchase-Account increases from 2000 to 1500(the input workload for the Authenticate scenario is assumed to be fixed), the computational delay resulted from assignment of three busy objects to N1 outweighs the communicational delay resulted from accessing R remotely by iis (Hence moving iis to N2 in deployment d1500). Subsequently, by increasing the input workload, the algorithm makes trade-offs between communicational and computational delays to find the best deployment. To show that dx is the near-optimal deployment corresponding to workload value x a simulation approach was chosen. An FSP model for deployment dx was generated. This model then was simulated using the LTSA tool and the resulting response times of this model were recorded for different input workloads. The simulation results for the case-study are presented in Figure 7. It is observed that when the input workload to the system is x, the deployment dx, found by our algorithm using the simulation results corresponding to x, outperforms (i.e. results in lower system response time) any other deployment dy found for input workload y (x^y).

Fig. 7. The system response times corresponding to each deployment for different input workloads

Conclusion

The main objective of a deployment optimization algorithm is to distribute the "execution load" of the software over available resources such that better performance is achieved. We believe that the "execution load" for a software should be estimated by runtime indicators rather than static ones. Moreover, the "execution load" is often changed by variations of input workload to the system. Therefore, the search for different deployments related to different input-workloads is reasonable. According to the results presented in Figure 7, it is concluded that better deployments (from the performance viewpoint) can be achieved by incorporating previous simulation statistics into the deployment algorithm. As the future work, we are enhancing our deployment algorithm to find the best deployment in presence of multiple replicas of objects.