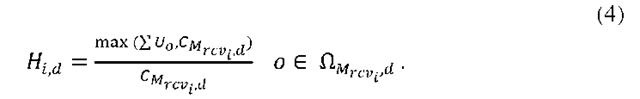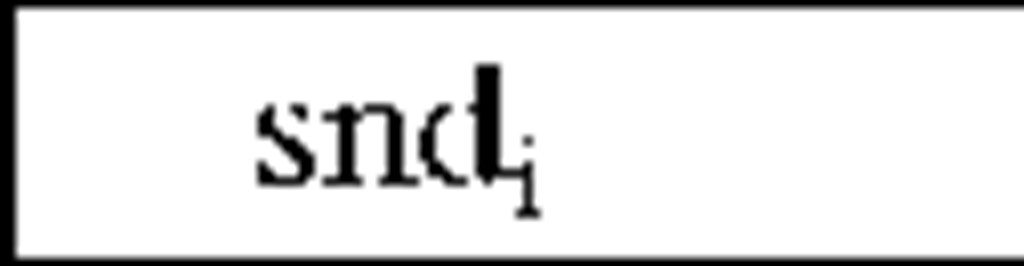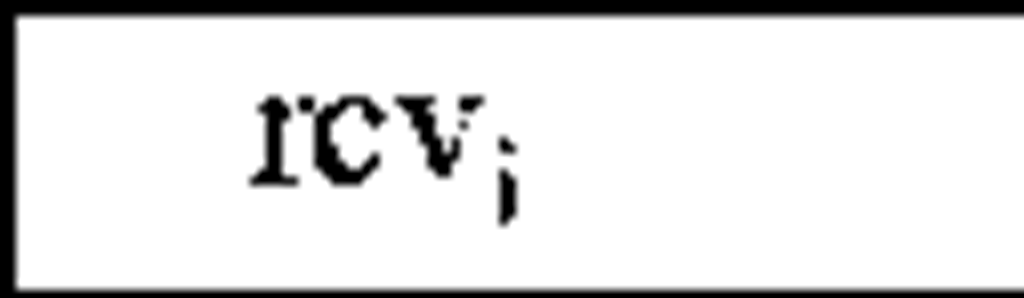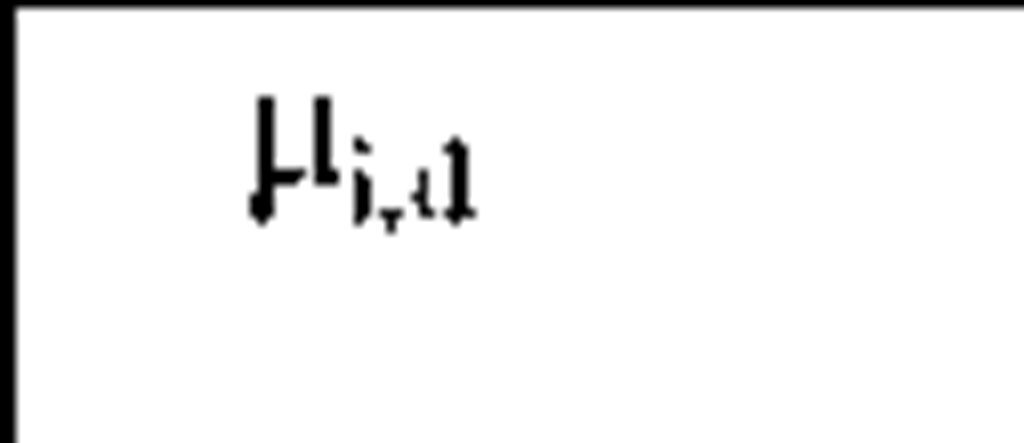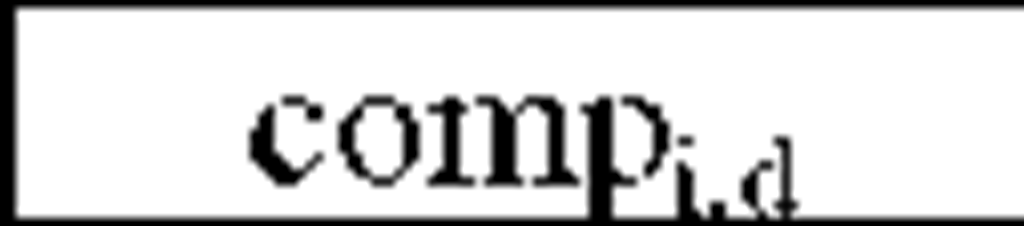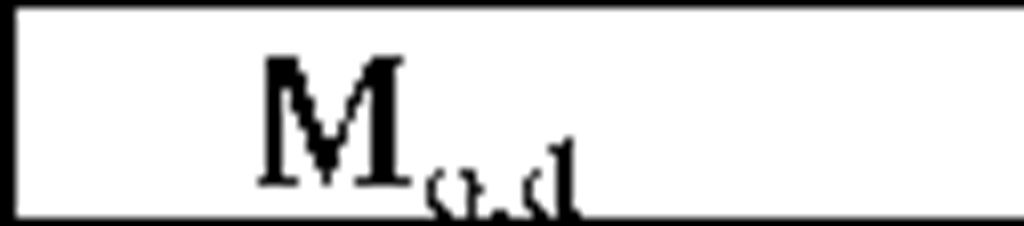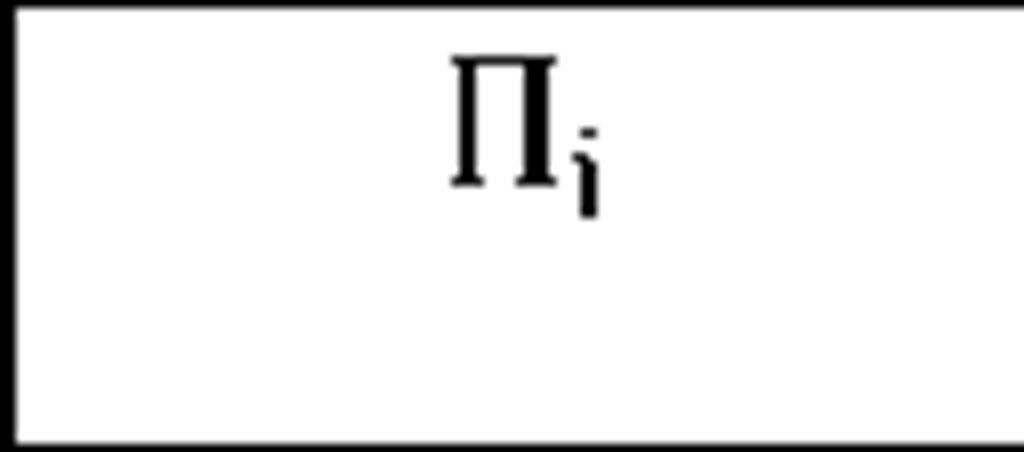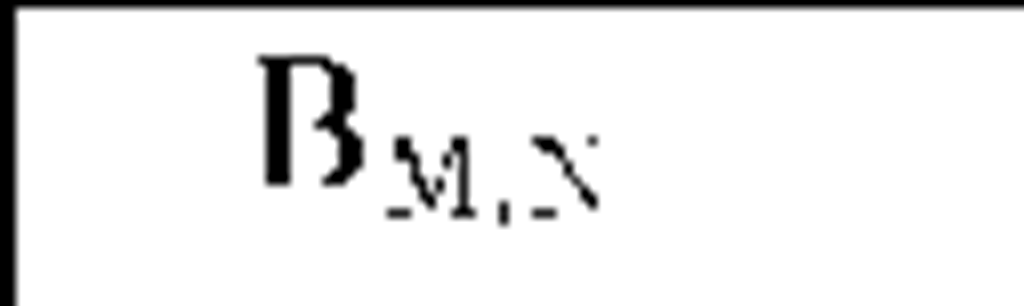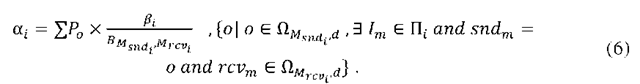Abstract
The correct deployment of software objects over the computational resources has a significant impact on the software performance. Achieving the optimal deployment manually is a tedious work as there are many different alternative solutions. In this paper a heuristic algorithm for optimizing the deployment of software objects is proposed which evaluates each deployment in the search space, considering its communicational and computational delays. In order to estimate these delays for an object deployment, our algorithm takes into account both the resource capacities and the execution load of the software for a given input-workload. The execution load of the software is measured by simulating the software use-case scenarios using the Finite State Process (FSP) models. From the simulation, the values of some metrics such as utilization, population and mean response times corresponding to the objects and threads participating in software use-case scenarios are recorded as the execution load indicators. These recorded simulation results are subsequently applied to estimate the goodness of a deployment in the search space.
Keywords: Software Performance Engineering; Object Deployment; Load balancing algorithm; Simulation.
Introduction
The performance of a distributed software system has always been of critical importance to the designers of such systems. Software Performance Engineering (SPE) aims at detecting and predicting performance problems at the early stages of development process by evaluating the software design or deployment using simulation, modeling or measurement [1]. There has been many works in automatic generation of performance models from software architectural models and then analyzing these generated performance models to locate the performance problems [2][3]. In order to solve these performance problems at design level, one approach is to manually optimize design decisions represented in performance models [4]. However automated techniques for optimizing the distributed software design or deployment with respect to performance have not been researched much so far [1]. One of the important factors affecting the performance of a distributed software is the way that software objects or components are assigned to the computing resources. For instance, deploying certain objects on the same computing node eliminates the network delay caused by message passing. Co-locating objects and resources they may need such as files, devices or special network links can also reduce the network delay. Furthermore, careful assignment of object replicas can lower the overall network delay caused by remote access to those replicas from other objects. The evaluation of each object deployment within the search space requires estimating the "communicational delays", as a result of remote communication among objects, and the "computational delays", as a result of sharing the same resources by deployed objects(i.e. resource contentions), corresponding to that deployment. In the field of deployment optimization, estimating these delays using only resource capacities ( e.g. CPU Ins/sec or link bandwidth) has been research in many previous works.
The main contribution of this paper is to incorporate the software execution load statistics in evaluating the communicational and computational delays of a given deployment during the optimization process. To achieve this, the value of some metrics such as object utilization, number of object or thread instances and mean response times of object invocations are required and obtained by simulating the intended use-case scenarios before applying the deployment algorithm. The simulation is performed by transforming each use-case sequence diagram, annotated with performance information according to the UML Profile for Schedulability, Performance and Time (SPT profile) [5], into a set of Finite State Processes (FSP) [4] and then executing them by means of a discrete event simulator tool. The proposed optimization algorithm is a hill-climbing algorithm that not only considers the processing and bandwidth capacities of network resources when evaluating an object deployment, but also takes into account other aspects affecting the performance such as the possibility of concurrent execution of objects and threads.
Related Works
Most SPE researches are focused on analysis of an existing performance model and there are few works that fall in the category of performance optimization of software. In [6] a Response Surface Method (RSM) for optimizing software performance indicators in presence of simulation results is proposed and its usefulness for minimizing total cost in a capacity planning problem is evaluated. However the usefulness of this method for complex optimization methods such as deployment problem has not been researched. In the field of deployment optimization, which is the main focus of this paper, there are some previous works: [7] is one of the earliest works in the field of deployment optimization in which a static task allocation method is proposed. However, they have not studied the effect of incorporating the software execution load statistics in the allocation procedure. In [8] a comparison between two deployment optimization methods: Binary Integer Programming and Genetic algorithm is presented. While reaching an optimal deployment, in this approach only the number of messages between components is minimized. In [9] a Linear Integer Programming-based method is used to find the optimal deployment of a set of components over computing resources. In this approach the main objective is to minimizing the computing and network delays. In [10] a deployment strategy for software objects based on placing the most communicating objects in the same machine is presented. To achieve this, an object graph construction algorithm and a partitioning policy for this graph are presented. In [11] the optimization of architectural models for multiple quality criteria using evolutionary methods is presented. Here, data transmission reliability and communication overhead are the only quality criteria considered. However, our work considers the "computational delays" in addition to the communicational overheads to achieve the best performance. In [12] a multi-criteria genetic algorithm for optimizing the software architecture for performance, cost and reliability is presented. In this work, the search for the optimal architecture is performed considering a number of degrees of freedom. It means that the architecture can change only along directions that preserve the functionality (e.g. changing the deployment or choosing among a set of alternative components with the same interface). In this work for evaluating the performance of each solution (architecture) within the population, the genetic algorithm generates an LQN instance from the architecture model and analyzes it using a solver. This is very time consuming method and cannot be applied to a large software with many components. However in our work the evaluation of each deployment is performed using a fast performance function (see section 4) based on previous simulation statistics. In overall, previous works in the field of automatic deployment is dedicated to the placement of software components over a set of computing nodes without considering the effect of execution load statistics when computing the communicational and computational delays for a deployment. In contrast, in this paper a methodology for deployment optimization of a set of objects, collaborating to realize some performance-constrained use-cases, using previous simulation records is presented. Minimizing the network delay between components, which is the focus of many previous works, is crucial however is not sufficient. Imagine that you put two components c1 and c2 on the same node N to reduce the network delay in between, however by doing this you might have increased the overall response time due to limited capacity of node N.
Deployment Methodology
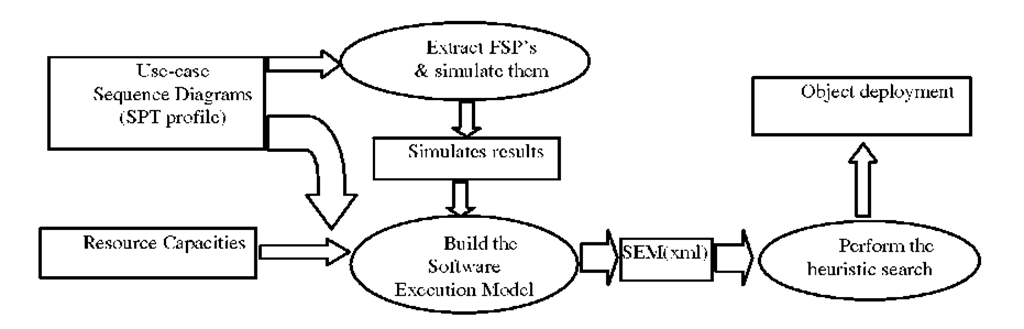
The main objective of many existing deployment optimization algorithms is to distribute the "execution load" of the software over available resources such that better performance is achieved. However in these algorithms the "execution load" of a software is estimated poorly (for example in [9] the number of instructions in each component or task is assumed as its load). We believe that the "execution load" for a software should be estimated by runtime indicators rather than static ones. Since we are solving the deployment problem at the early stages of software development and the only thing we have at this stage is the software models (not code), a simulation method has been chosen to predict the "execution load" of software. We have estimated this load for a use-case scenario based on these runtime indicators: (1) The population of objects or threads, (2) The mean response time of active objects and (3) the average utilization of objects. These three indicators are measured by simulating use-case scenarios for different input rates. Since the three indicators mentioned above may have different values for different input workloads to the software, it is concluded that the "execution load" of a software changes for different input workloads. Therefore it is reasonable to find an optimal deployment for each input workload separately (see the experimental results). Figure 1 gives an overview of the deployment methodology presented in this paper.
Fig. 1. The deployment methodology
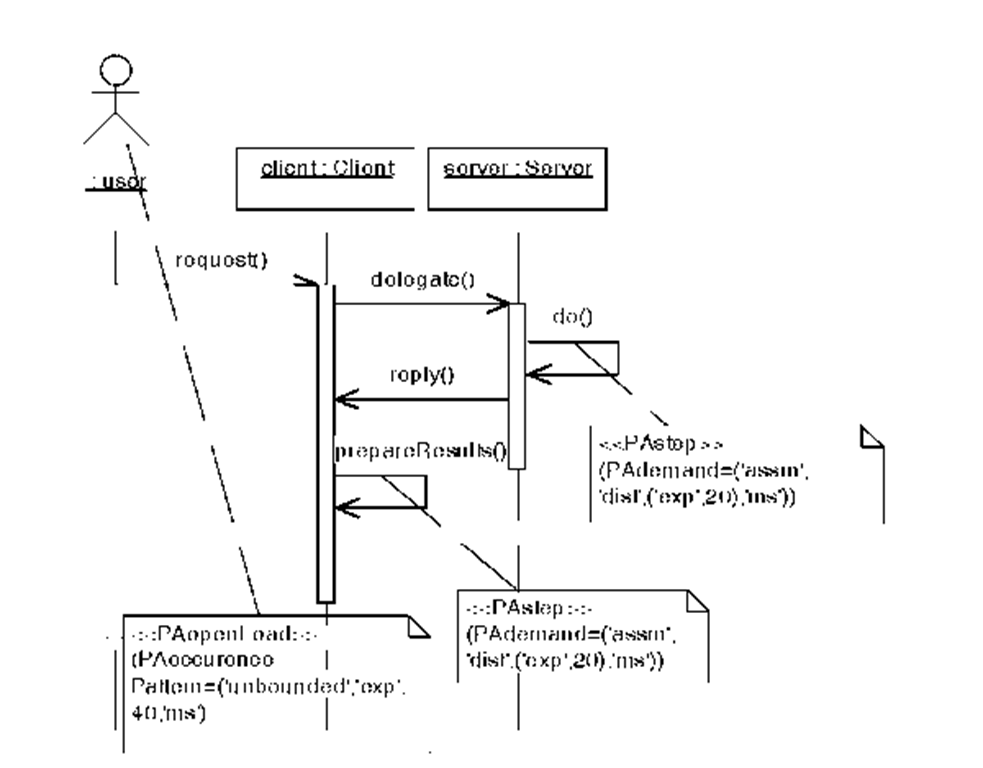
At the first step, corresponding to each object within the use-case sequence diagrams a Finite State Process (FSP) is created. Creating FSP’s is a mechanical task and can be performed by means of automated tools such as LTSA [13]. The resulted FSP’s are then composed together and used to perform the simulation (based on the discrete-event simulation model). The simulation results include measured values for metrics such as object utilization, mean response time and object population. These values are good indicators for the software execution load. The next step is to build an xml document called Software Execution Model (or SEM for brevity) for the use-case scenarios. Specifically, the following information is included in SEM: (1) Scenario Call Flow Graph: The flow of method calls among objects within a scenario. For each invocation Ii in the scenario, the set of all blocking and non-blocking calls within Ii, the synchronization point of Ii and the set of all concurrent invocations with Ii are also kept. (2) Scenario execution Loads: which are the measured values for metrics as object utilization, mean response time and object population. (3) Resource Capacities: including processing capacities and link bandwidths. SEM can be generated automatically from the use-case sequence diagrams. In the last step, a hill-climbing algorithm seeks the optimal deployment of software objects regarding the information contained in SEM. The objective function of this algorithm is explained in the next section. The simulation is performed by creating a set of Finite State Processes each corresponding to an object in the use-case sequence diagram. For instance the sequence diagram shown in Figure 2 is modeled by the following three communicating processes:
USER=(request->< ?exp( i.0/40j?>next->USER).
CLIENT=(request->delegate->reply-><?exp(i.0/20)?>prepareResults->CLIENT).
SERVER=(delegate-><?exp(i.0/20j?>do->reply->SERVER).
The actions in the above processes, e.g. request, delegate, reply, prepareResults and do are encoding the messages specified in the sequence diagram. In addition, the time delays specified in the sequence diagram using SPT annotations, are translated into time delays in the corresponding FSP processes using <?exp(1.0/x)?> shorthand by which an anonymous clock is set to run down for an exponentially-distributed time with mean x mili-seconds. The resulting FSP,s then were simulated by means of LTSA.
Fig. 2. Sample sequence diagram annotated with performance information
Performance Function
In order to find the optimal object deployment from the performance view point, the heuristic search algorithm (mentioned above) evaluates each possible deployment d within the search space using a Performance Function,named 0. Assuming that 0i(d) be the estimated execution time of invocation Ii (an arbitrary invocation within the scenario of use-case u), 0s(d) will be the estimated execution time of use-case u for which Is is the starting invocation. The optimal object deployment corresponding to a software with n use-cases ubu2…un is the one for which the weighted average
is minimal where
are the starting invocations of use-cases u!,u2,…,un respectively. The coefficients fi,f2,.,fn indicate the relative significance of use-cases u1,u2,..,un from the performance view point(defined by the software architect).
The performance function 0i(d) is a recursive function that estimates the response time of invocation Ii when the object deployment is d. Assume an invocation Ii which is called within the body of invocation Is. Theestimated execution time of Is for a given deployment d is calculated as:
where Ts is the estimated execution time of all statements within Is except method calls. Depending on deployment d, the caller and callee objects of Ii may reside on the same or different nodes. In the latter case, Invocation Ii is a remote invocation and some communicational delay should be added to the sum:
where ai is the communicational delay corresponding to the remote invocation Ii. In the former case the communicational delay is zero. The two cases can be combined in one relation:
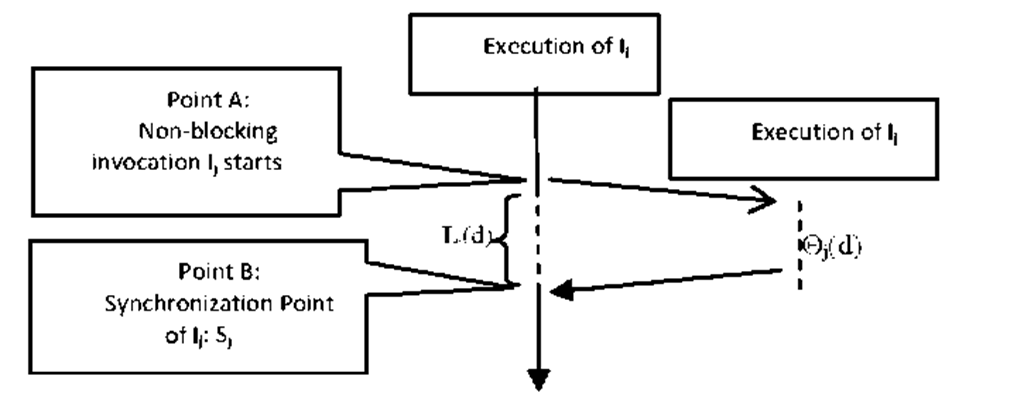
Where ^i,d is a binary decision variable which is set by the deployment algorithm regarding deployment d. If the caller and callee of Ii in d are located on the same node ^i,d is set to 0, otherwise it is set 1. Generally, the method calls inside invocation Is are categorized into blocking and non-blocking. For each blocking invocation Ii within Is, the value of 0i(d) is added to the total execution time of Is. For each non-blocking invocation Ij within Is, there is a synchronization point within Is at which the results of Ij are received by Is(see Figure 3). The amount of time that Is should wait at the synchronization point of Ij to receive the invocation results, is added to the total execution time of Is. This wait-for-result delay corresponding to the non-blocking invocation Ij is denoted by Sj . As shown in Figure 3, in a non-blocking invocation, the caller continues executing until reaching the synchronization point. Assuming that Lj(d) be the estimated execution time of those statements within Is located between the initiation point and the synchronization point of Ij regarding deployment d (as shown in Figure 3), the wait-for-result delay Sj is simply calculated by subtracting Lj(d) from the total turnaround time of Ij:
Where aj is the communicational delay of Ij when it is a remote invocation (i.e. |ij,d=1). Note that computing the value of Lj(d) may require that the estimated execution time of other invocations (or synchronization points) located between the initiation point(Point A in Figure 3) and the synchronization point of Ij(Point B in Figure 3), be computed recursively.
Fig. 3. A non-blocking invocation and its synchronization point
In addition to the communicational delay corresponding to a remote invocation (blocking or non-blocking), another delay, called computational delay, is also important when evaluating a given deployment d. The Computational delay of an invocation Ii is defined as the delay in execution of Ii due to sharing the machine on which Ii is executing with other concurrent invocations. Assume that Ti be the estimated execution time of statements within Ii when the whole processor is dedicated to it, the computational delay compi,d of Ii regarding the deployment d is defined as follows:
In the above relation, the value of Ti is multiplied by factor Hi,d to magnify the estimated execution time of invocation Ii according to the utilization of the machine on which Ii executes regarding deployment d. If the total utilizations of the objects located on this machine exceeds the machine capacity (denominator of the fraction in relation 4) the value of Hi,d become greater than one, otherwise it equals 1:
The description of symbols used in this relation and the subsequent relations are summarized in Table 1. Suppose Is be the starting invocation of use-case u and the set of all invocations within Is is partitioned in two blocking and non-blocking sets. Relation (1) for computing 0s(d) is generalized as follows:
Table 1. Descriptions corresponding to symbols and parameters used in equations
|
Parameter |
Description |
 |
The capacity of computational node N which is the number of installed processors on N multiplied by 100 |
 |
The utilization of object o. This value is obtained from the simulation |
 |
The average number of instances of active (or reactive) object o which are running simultaneously in the system. This value is obtained from the simulation |
 |
The mean response time of invocation Ij. This value is obtained from the simulation |
 |
The caller object of invocation Ij |
 |
The target(callee) object of invocation Ij |
 |
A binary decision variable. If ^ equals 0 the caller and callee of Ij are located on the same machine, otherwise they are deployed on different machines |
 |
The communicational delay of Ij |
 |
The computational delay of Ij regarding deployment d |
 |
The amount of required bandwidth for transferring parameter values of invocation Ij over a link in a unit of time (1 ms) |
 |
The machine on which object (or resource) o is located regarding deployment d |
 |
The set of objects located on machine M regarding deployment d |
 |
The set of all invocations in the scenarios which may execute in concurrent with Ij. It is assumed that nj always includes Ij |
 |
The link bandwidth between machine M and N(KB/s) |
In relation (5), Ts is the estimated execution time of all statements within Is except method calls. When there is no method call within Is, the value of Ts is equal to RTs which is obtained from the simulation results( see Table 1). In relation (5), a denotes the communicational delay for invocation Ii and is included in the total execution time when the value of | i,d is 1, which means the invocation Ii is a remote invocation according to deployment d. This communicational delay is defined as the amount of time required for transmitting parameter values and receiving the return values of Ii over the network link which connects the sender and the receiver node of Ii (Msnd. denotes the sender and Mrcv. denotes the receiver node of Ii). To calculate this delay, first consider that the amount of bandwidth between machines Msnd. and Mrcv.(denoted by BMsnd Mrcv,) is shared among all invocations that may use this bandwidth concurrent with Ii. Therefore, the available bandwidth for Ii is BMsnd Mrcv, divided by the number of objects located on Msnd. on condition that the object is the sender of an invocation concurrent with Ii. Hence, value of ai is calculated as follows:
