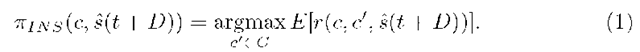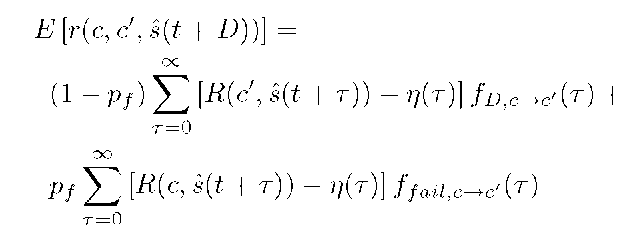Abstract
A dynamically changing state of the run-time environment impacts the performance of networked applications and furthermore influences the user-perceived quality of the applications. By migrating the application between the user’s devices that give different user experiences, a good overall user experience can be maintained, without loosing the application session. It is non-trivial for a system to automatically choose the best device for migration. The choice must maximize the user experience quality and take into account that a migration delays the user’s work-flow and even may fail. Moreover, the environment state is not directly observable, and needs to be estimated which leads to inaccuracy. We model the automatic migration trigger as a stochastic optimization problem and we propose to use a hidden Markov model combined with a Markov Decision Process (MDP) to solve the problem. The solution generates policies to choose target device for migration that gives the optimal user experience. We analyse these policies in simulation experiments and derive conclusions on which scenarios the model-based approach performs better than a greedy approach, also when considering inaccurate state estimation.
Keywords: migratory applications; configuration choice; Markov decision processes; quality-of-experience.
Introduction
A dynamically changing state of the run-time environment impacts the performance of networked applications and furthermore influences the user-perceived quality of the applications. For example, if excessive packet loss on a wireless connection or in a network router reduces the end-to-end throughput, a video streaming application may experience glitches or outage periods. In addition, users have access to many different types of devices with network access that can run the same applications. Therefore, we investigate methods to move active application instances between devices to maintain a good user experience in scenarios with dynamic networks. The process of moving the application is called migration [1]. We consider migratory applications that can be moved between the user’s devices. We define a configuration as the combination of an application running on a device and the settings of the device (CPU, network interface, display resolution, etc.). A configuration gives the user a certain experience quality, influenced by the state of the environment. A migratory application has several available configurations and the objective of the migration is to change the active configuration. Migration is performed without restart of the application session, allowing the user to continue the work-flow after migration. Migratory applications run on top of a migration middleware (such as described in [2]). The purpose of the middleware is to trigger migration automatically and orchestrate the migration procedure. The orchestration procedure takes time which interrupts the user’s work-flow and degrades the experience quality. The duration of the migration procedure depends on the migration type, which can be strong or weak. In a strong migration both application code and state is transferred, where in a weak migration only parts of the application stack are transferred [1]. We consider the migration procedure as atomic and our models are independent of migration type. Different types only produce different model parameters values in terms of migration delay distribution and failure probability.
An automatic migration trigger must balance the trade-off between configurations with high experience quality and the reduced experience quality caused by the orchestration procedure. The triggers are based on the environment state. However, the true state is not always observable and must be estimated from observable parameters. If state estimation is inaccurate, wrong migrations are triggered, which interrupt the user and may end up in worse configurations. To balance the trade-off, we treat the automatic trigger as a stochastic optimization problem. We model the environment behavior, the state estimation, the application experience behavior and the migration procedure as stochastic processes. The stochastic models are used to generate policies that specify in which state to trigger migration and which configuration to migrate to. We evaluate two different policy generation approaches: 1) a greedy approach that optimizes the user experience in the next evaluation step and 2) a Markov Decision Process (MDP) approach which can account for the effect of future decisions and optimizes for the long-term user experience. We design an enforcement framework around the policies with functions to observe the environment, estimate the environment state and trigger and perform migration. Based on a simulated full migration scenario, we evaluate the effect on the experience quality of: 1) the estimation approach, 2) the policy generation approach and 3) the environment behavior. Through result analysis we illustrate the usefulness of including future decisions and the impact of inaccurate environment state estimation.
The concept of migration upon environment state changes is increasingly important. With the rise of dynamic adaptive systems (component-based systems which are able to change their composition, [3,4,5,6,7]), applications may be deployed in environments for which they were not originally designed. The application domain can be expanded if they have underlying support to choose the optimal configuration for such unknown environments. The optimal configuration is also relevant in dynamic applications that interact with users [8] since the success of these applications depends on the user’s experience. Previous research has shown that model-based policy generation approaches allow for robust decisions; video stream application stream decoding [9], placement policy of processing tasks in virtual environments [10] and QoS management policies [11]. The quality of the user’s experience is modeled by reward functions that map physical properties into experience quality. Methods to derive reward functions are covered in detail in existing literature. For instance mapping network properties into quality of multi-media applications can be studied in [12,13,14] and is not treated further here.
The rest of the paper is structured as follows. In section 2, we present background details of the migration process. In section 3, we describe a model of the migratory system to base the decision framework design on, which is presented in section 4. Then, in section 5, we describe the analysis of the dependencies between the framework parameters and the performance of the policy generation approaches. The paper is concluded in section 6.
Background on the Migration Process
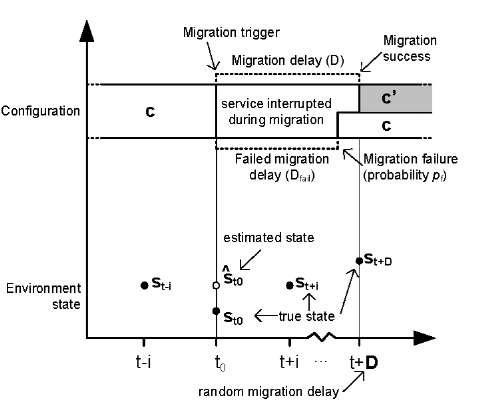
The events of a migration process between two devices are illustrated in Figure 1. The migration framework is realized as a middleware that contains a decision framework that monitors the state of the environment and automatically determines the best configuration to use (see [2] for more details). If the chosen configuration is not equal to the one currently applied, a migration is triggered. The application instance on the source device is paused and a state object, with sufficient information to resume the application elsewhere, is extracted and downloaded onto a central migration server. As the download may be performed over any available network connection, the performance of the network connection affects the duration of the download, and hence, the duration of the migration. Also, any faults that can occur on the network connection may cause the download or migration signaling to fail. After the state is downloaded, a new application instance is initialized on the target device. The state object is then uploaded to the target device and inserted into the new application instance. To complete migration, the new instance is resumed in the original state.
Model of the Migratory Framework
A model of the migratory framework is illustrated in Figure 2. We specify the environment as a set of N states, S = {si,…, sN}. The states are abstractions of the environment parameters, which are considered relevant if they impact the performance of the application or the migration process. We model the behavior of the environment as a Markov model. P(si, Sj) denotes the probability of a transition from state si at time t to state Sj at time t +1. The next configuration of the application is decided periodically by the migration middleware. A set of M configurations, C = {ci, …,cm}, constitutes the set of possible next configurations. The middleware has to decide which configuration cC to change to from the current configuration c. If
a migration
is attempted.
Fig. 1. Migration process events
Fig. 2. Time-line migration process
The migration duration in time-units, D, is random and characterized by a distribution
that depends on the size of the state object that needs to be transferred and the environment state. If the migration is successful, the application is in configuration C after time D. If the migration fails, with probability pf, the duration until the system returns to configuration c may be characterized by a different distribution 
For simplicity, we assume
in this paper.
Furthermore, the delay may be dependent on the environment state, however we consider them independent in this work.
Design of the Decision Framework
The decision framework consists of several components required to generate and enforce decisions. Figure 3 shows the components of the framework. The components are active at different times in the migration process. Decision policies are generated offline in the policy generation component. A decision policy, n(c, s), specifies which configuration to choose when in configuration c and in state s. Two approaches for policy generation are evaluated in this work. The first approach is greedy and generates policies that optimize for the best immediate experience. We call this approach instantaneous. The second approach is based on a Markov Decision process which generated policies that optimize for the best long-term average experience. Both approaches assume that the state of the environment is known when the decision is made. However, this is not always possible since states that are not directly observable may affect application performance. In such cases the true environment state is hidden to the enforcement component, and in order to enforce decisions from a policy, the true state must be estimated based on parameters that can be observed. When the system is online, the environment state, s(t), is estimated in the state estimation component based on observations made by the observation component. The estimated state is used to enforce decisions from policies in the policy enforcement component.
Fig. 3. Overview of the decision framework in the migration middleware
State Estimation and Prediction
To enforce a policy online, the current application configuration c and the estimated environment state s(t) must be known. The observable parameters are sampled at periodic intervals during run-time and the most likely environment state is estimated. We investigate how two different estimation methods perform in the decision framework, namely a threshold approach (TH) and a hidden Markov Model (HMM) approach [15]. The two methods estimate the most likely environment state s based on observable parameters. The TH method assumes a direct mapping between observations and environment state. The HMM method models the environment as a Markov model and assumes a stochastic relation between the true state and the observed parameters. During run-time, the Forward-Backward algorithm is used to calculate the probability distribution over the set of states given the sequence of previous and current observations. By using a Marginal Posterior Mode (MPM) estimate [16], the most likely state of the environment can be calculated. Transition probabilities of the HMM are the same as the environment model P. Observation probability distributions, P(o5s|S), depend on how the environment affects the observable parameters. Concrete values for both matrices are specified in the simulation model.
To predict the most likely estimated state at time t + D (after migration), the behavior of the Markov model is used, such that the predicted state s(t + D) is set equal to the most likely state D steps in the future. This is calculated from argmax ei ■ PD, where ei is an 1xN vector, where element i is equal to one if si is the most likely system state and the other elements equal zero.
Reward Model
Reward is defined as a combination of the satisfaction of experiencing a certain application quality and the dissatisfaction of the interruption from migration. Reward of an application configuration in a certain system state is characterized by R(c, s). The dissatisfaction is characterized by two parameters of the migration process; the probability of migration failure, pf and the migration delay, D. These two parameters influence the user experience negatively and can therefore be used to characterize how performing a migration should be penalized. We represent the penalty of waiting during migration, n, as a function of the waiting time n(D). The penalty function can have different shapes (linear, logarithmic, quadratic, exponential) representing different user dissatisfaction patterns. In our work, we define the function linearly as n(D) = —a D, where a is a constant and represents the reduction in reward per time-step experienced by the user while waiting on the migration to finish. The linear function is chosen for simplicity, and may be changed to other shapes.
Instantaneous Policy Generation
The instantaneous (INS) approach chooses the configuration c’ that generates the highest expected reward for the predicted state estimate after the migration c ^ c’, such that
The reward expression r(^) represents the reward of migrating from c to c’ when the predicted state after migration is s(t + D). The expression includes the failure probability and random migration duration as follows.
The INS approach is greedy. It is also conservative, in the sense that it maximizes the reward for the immediate state after migration (positive), but accounts for all migration penalty during migration (negative).
Markov Decision Process Policy Generation
The Markov Decision Process (MDP) approach can consider the effect of future decisions on the long-term average reward and generate a policy with the decisions that optimize that. An optimal policy, nMDP(c, s), can be calculated offline using the MDP before running the application. We use value iteration with a finite window of 1000 future decisions to find the optimal policy by use of the Bellman equation for dynamic programming. The finite window is applied to enable comparison to the INS approach. The values of the window size was found through experiments and is large enough for the policies to converge, meaning that a larger window will only affect computation time, but not change the policy. See [17] for more details on the MDP framework, dynamic programming and value iteration.
The general form of the Markov model used in our decision framework is depicted in Figure 4.a. For each available configuration we assign a reward function R(c, s) that maps a reward value to each environment state for a given configuration. There exist different reward functions for the different configurations. In Figure 4.b the scenario of migrating between configurations c ^ c’ is depicted. The actions of the MDP map directly to the available configurations, which can be chosen at each time-step. To model the migration process, an intermediate delay state is introduced between the configurations. When the migration is triggered, the system enters the delay state with probability 1. The reward model of the delay state is defined according to n(D), which means that in the linear case of this framework, the reward of the delay state is simply a. In the delay state the migration may be further delayed with probability pd, fail back to c with probability pf (1 — pd) or succeed to c’ with probability (1 — pf) (1 — pd). The definition of pd is based on the migration delay D. When D is geometrically distributed then
where D is the mean migration delay.
Fig. 4. Model of the migratory system. (a) is the general evolution where the reward (R) only depends on the environment if the configuration is fixed. (b) shows how a migration c ^ C may change the active configuration and thereby the reward function if successful.
Case Study and Numerical Results
We evaluate and compare the performance of the different estimation methods and generation approaches by simulating the migration framework. The MDP is solved using dynamic programming and the scenario is simulated (instaed of solved analytically) to capture the behavior of the entire migration platform and application quality. First, we systematically analyse the differences between two policy generation methods to learn where they are different, and how the difference impacts the application quality. Next, we evaluate the accuracy of the two state estimations methods, including the ideal estimator as reference. Finally, we analyse two example scenarios of the entire framework to learn how the different parameters of the full framework impact the application quality. We evaluate three state estimation methods combined with the two policy generation methods in two different scenarios, which reflect two different network conditions.
Simulation Model
The environment is modeled as a network with two states, representing a normal and a congested network, S = {N,C}. P, the transition behavior within S, is specified by p, the probability of a transition from N to N, and q, the probability of the transition from C to C, as specified in Table 1. The application is a video streaming application with two available configurations on two difference devices; D1) high definition on large display device, and D2) standard definition on mobile device with smaller screen), C = {D1,D2}. The reward values of the two configurations, R, are listed in Table 1. These values express that the user gets a higher perceived quality with increasing resolution on the large display device (i.e. R=4 for (c,s)=(1,1) compared to R=3 for (c,s)=(2,1)). Moreover, the impact of packet loss is larger when c = D1 than c = D2 because the higher resolution requires more available bandwidth on the large display. As migration penalty values, we use pf =0.1 and use a geometrically distributed delay D with parameter pd = 0.95. This characterizes a mean migration delay of 2 seconds, when time-unit per time-step is 100ms (equal to D = 20). The failure probability and delay mean are sampled from experimental work on migration prototypes, described in detail in [18]. For the dissatisfaction function n(D) = —a ■ D, we use a = 0.01, which has been determined a reasonable value through experiments, as it depends on a combination of the scale of the rewards and the mean delay. The parameter values are summarized in Table 1.
For network observations we use packet loss ratio in both scenarios with two possible states (low, high), representing measurable packet loss in a congestion-prone network, obs = {L, H}. The probability distributions of the observations in each network states, b, are listed in Table 1. The distributions reflect the situation where high packet loss is primarily observed when the network is congested. This would be the case when buffers in a bottleneck router overload and packets are dropped consequently, but the network otherwise is stable. We simulated 30 runs of the network model in 10000 steps and obtained sequences of true network states s(t), observations from the threshold estimator and estimated network states s(t) from the HMM estimator.
Table 1. Model parameters of the different components used in the evaluation
|
block |
description |
name |
value |
|
environment |
transition probabilities |
|
{0.01, …, 0.99} |
|
estimation |
observation matrix |
b |
 |
|
migration model |
reward waiting penalty mean delay failure probability |
R(c,s) a D Pf |
 |
|
MDP |
window size |
w |
1000 |
