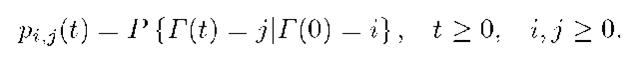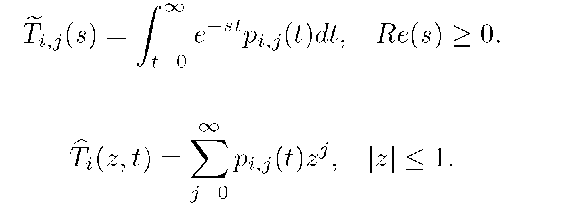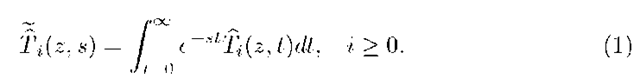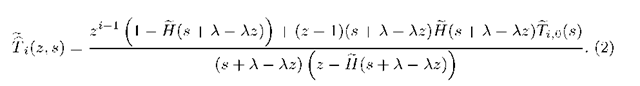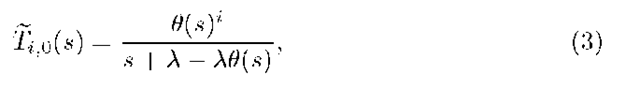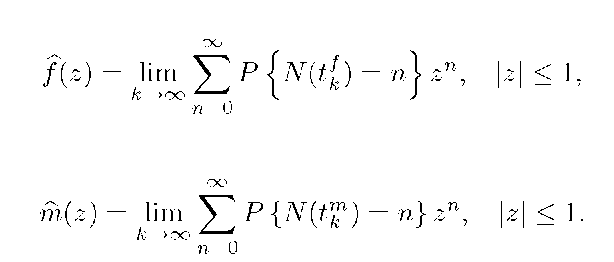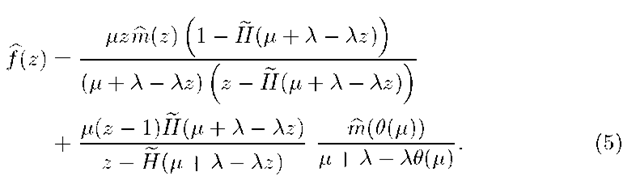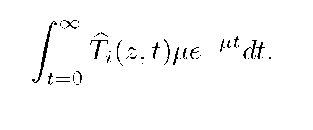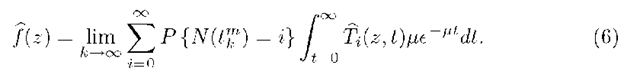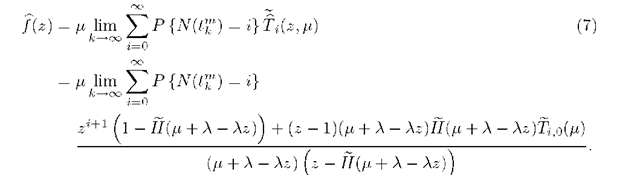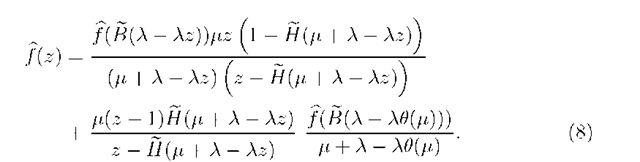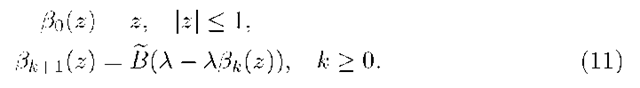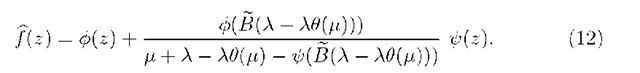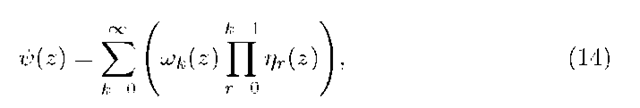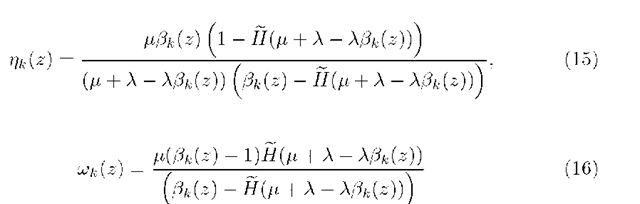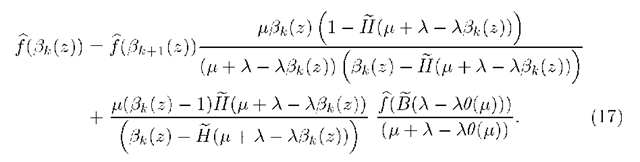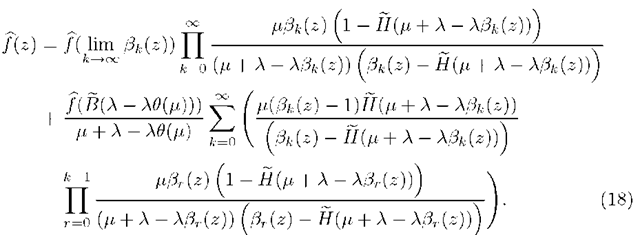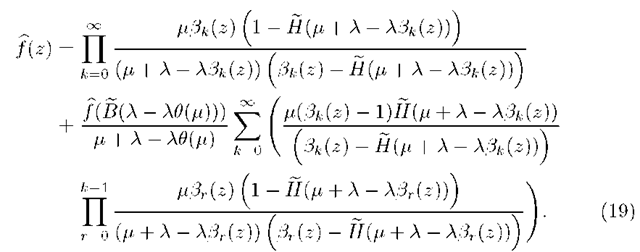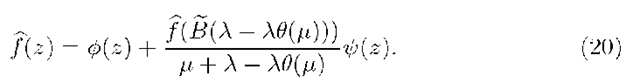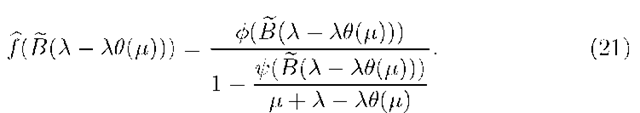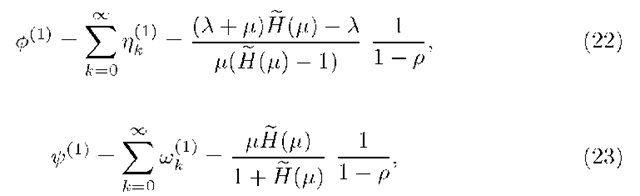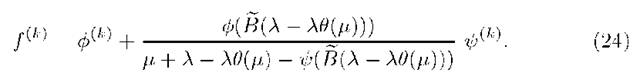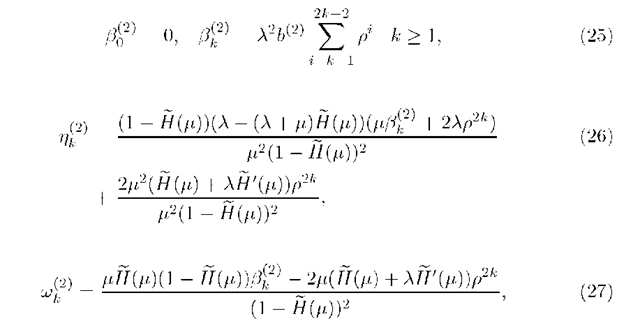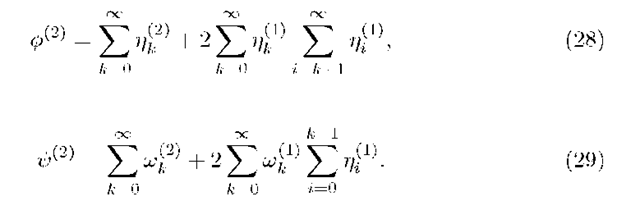Abstract
In this paper we consider the analysis of an M/G/1 queue with working vacation. In contrast to the previous literature where the working vacation starts when all customers are served (exhaustive discipline) we consider the case where the vacation period starts when the customers present at the system at beginning of the service period are served (gated discipline). The analysis of the model with gated discipline requires a different approach than the one with exhaustive discipline.
We present the probability-generating function of the number of customers in the system and the Laplace-Stieljes transform of the stationary waiting time.
Keywords: queueing theory, vacation model, working vacation.
Introduction
Working vacation (WV) is an extension to the regular vacation model, where the server is switched off during the vacation. In WV systems, instead of completely stopping the service at the beginning of the vacation period, the server continues serving the customers with a different service rate. In practice the service rate during WV is lower than the one during service period, but it is not a modeling restriction. WV models are suitable to describe practical system features like the effect of a lower intensity administrative task of the server, e.g. a safeguard service, following an active period. In the multiple working vacation (MWV) model a vacation period is followed by another vacation period if the server finds the system empty upon returning from vacation.
The regular vacation model is a special case of the working vacation model with zero service rate during vacation. Thus the working vacation model is a generalization of the regular vacation model and hence, as expected, its analytical complexity is somewhat higher than the one of the regular vacation model.
Vacation models with Poisson arrivals have been intensively studied in the last decades. For such models and for their solution we refer to the survey of Doshi [4] and to the fundamental topic of Takagi [16].
The WV policy has been introduced by Servi and Finn [13] in 2002. They applied the M/M/1 queue with multiple working vacations to model a Wavelength-Division Multiplexing (WDM) optical access network. They derived the probability-generating function (PGF) of the number of customers in the system. Baba [1] generalized this model to a renewal input GI/M/1 queue with working vacations and derived the number of customers at customer arrival epochs and at arbitrary time. Wu and Takagi [18] generalized the model of Servi and Finn to the M/G/1 queue with working vacations. They provided a numerical solution for computing the distribution of the number of customers in the system. Liu, Xu and Tian [10] proved that the well-known stochastic decomposition property of the vacation queues [5] holds also for an M/M/1 queue with working vacations. Recently Li and Tian with co-authors in [9] and [8] applied the matrix analytic approach subsequently to an M/G/1 queue with exponential working vacations and to its extension to batch arrivals, respectively. In all the above-mentioned working vacation queueing models the exhaustive discipline has been applied, i.e. the vacation starts, when the queue becomes empty.
In this paper we analyze the M/G/1 queue with exponential working vacations, but in contrast to the above references we consider the gated discipline. According to this discipline only those customers are served during the actual service period, which are already present at the beginning of the service period. Thus the customers arriving during a service period are present at the beginning of the next vacation period. A potential application of this model is the analysis of an Internet Protocol (IP) over WDM optical access network (see in [11]).
The contribution of this paper is the queueing theoretic analysis and the results for the M/G/1 working vacation queueing model with gated discipline. In the first part of the analysis we establish a functional equation for the PGF of the stationary number of customers at the end of vacation period, for which we utilize known results for the transient behavior of the M/G/1 queue. We solve this equation by using a convergence property of sequence of scalar probability functions (see [7] or [6]), which results in the expression of the PGF of the stationary number of customers at the end of vacation period. In the second part of the analysis we establish a relation for the PGF of the stationary number of customers at an arbitrary epoch. For the analysis we apply several elements of the methodology of [18]. The main results are the expressions of the PGF of the stationary number of customers at an arbitrary epoch and of the Laplace-Stieljes transform (LST) of the stationary waiting time.
The change of service rate is an important feature of the WV models. In the the WV model the service period ends in a service completion epoch. It means that the last customer served during the service period is served with the regular service time and the first one in the vacation period is served with the service time of the vacation period. In contrast to this the end of the vacation period is not synchronized with service completion. If a vacation period expires during the service of a customer the service period starts with repeating the complete service of the same customer but with the service time of the service period.
The rest of this paper is organized as follows. In section 2 we introduce the model and the notation. The stationary number of customers at the end of vacation are derived in section 3. The PGF of the stationary number of customers is given in section 4. The LST of the stationary waiting time is provided in section 5.
Model Description
We consider a queue with multiple working vacations and gated service. The customer arrival process is Poisson with rate A. Due to the gated service only those customers are served, which are present at the start of service period. The customer service times are independent and identically distributed. B, B(t), B(s), b, b(2) denote the service time r.v., its cumulative distribution function, its LST and its first two moments, respectively. The service during the service period is work conserving and non-preemptive. After finishing the service in the service period the server goes to vacation. The vacation period, V, is an exponentially distributed r.v. with parameter /. Note that the customers arriving during the service period are present at the start of vacation. According to the multiple working vacation policy the server serves the customers with a different service time distribution during the vacation period instead of completely stopping the service. The customer service times in the vacation period are independent and identically distributed. H, H(s), h denote the service time r.v. in the vacation period, its LST and its mean, respectively. If there is a customer under service at the end of vacation period, the server changes to another service rate, i.e. it interrupts the service and starts a new service on that customer with the customer service time B. If there are no customers in the system at the end of the vacation period, the server immediately takes another vacation period. We define the cycle time as a service period and a vacation period together. On this vacation model we impose the following assumptions:
A.1 The arrival rate, the mean customer service time, the mean vacation time and the mean customer service time in the vacation period are positive and finite, i.e.
A.2 The arrival process, the customer service times, the sequence of vacation periods and the customer service times in the vacation periods are mutually independent.
A.3 The customers are served in First-In-First-Out (FIFO) order.
We assume that the model is stable. Both the mean vacation time and the arrival rate are finite, thus only finite number of customers can be accumulated during the vacation period. Hence from the point of view of the stability only the service period has to be considered. According to this the model is stable if the arrival rate does not exceed the mean service rate
. Consequently the condition of the stability is p < 1, where we introduced the notation
The Markov Regenerative Process (MRP) framework (introduced in [12], Theorem 1) holds also for this model, since all the necessary assumptions are fulfilled. Thus the limiting distributions of the number of customers at different epochs and in different intervals are stationary distributions. Hence through this paper we use the term " stationary" instead of " limiting".
When y(z) is a PGF, y(k) denotes its k-th derivative at z = 1 for k > 1, i.e.,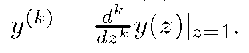 
The Stationary Number of Customers at the End of Vacation Period
In this section we derive the PGF of the stationary number of customers at the end of vacation period. We describe the evolution of the system over the vacation period in terms of PGFs of the stationary number of customers. For doing this we take the idea of utilizing the transient behavior of the M/G/1 queue from [18], which we recall first. The descriptions of the evolutions of the system over the vacation period and over the service period lead to a functional equation for the PGF of the stationary number of customers at the end of vacation, which we call the governing equation of the system. Afterwards we solve this functional equation by applying a convergence property of sequence of scalar functions.
Transient Behavior of the M/G/1 Queue
Let r(t) be the number of customers in the M/G/1 queue at time t for t > 0. Suppose that the queue starts to work at t = 0 and r(0) = i for i > 0. The transition probability describing the changes of the number of customers up to t is defined as
The corresponding Laplace transform (LT) and PGF are given as
can be explicitly expressed as ([14], p. 74, eq. (77))
Here Tii0(s) can be explicitly given as
where 6(s) can be determined from the equation
as its root with the smallest absolute value ([14]).
Evolution of the System over the Vacation Period
Let N (t) the number of customers in the system at time t for t > 0. Furthermore let tfk and t™ denote the end and the start of vacation in the k-th cycle for k > 1, respectively. The stationary PGF of the number of customers at the end of vacation, f (z), and at the beginning of vacation, m(z), are defined as
Let f = f(1) denote the mean of the stationary number of customers at the end of vacation. Similarly let m = m(1) denote the mean of the stationary number of customers at the start of vacation.
Theorem 1. In the stable M/G/1 multiple working vacation model with gated discipline satisfying assumptions A.1 – A.3 the m ^ f transition can be described as
Proof. The evolution of the number of customers in the working vacation can be described by the transient behavior of the M/G/1 queue starting with the number of customers present at the start of vacation. Assuming that the number of customers present at the start of vacation in the k-th cycle is i > 0, the PGF of the number of customers present at the end of that vacation can be expressed as
Unconditioning on the number of customers at the start of vacation and letting k tend to to gives the PGF of the number of customers at the end of vacation as
Applying the definition of
Applying (3) and the definition of m(z) in (7) gives the statement of the theorem.
Computation of f (z)
Theorem 2. The governing equation of the stable M/G/1 multiple working vacation model with gated discipline satisfying assumptions A.1 – A.3 is given in term of f (z) as
Proof. Under the gated discipline the number of customers at the end of the service period (= at the start of vacation) equals to the number of customers arriving during the service period. The PGF of the number of arriving customers during a customer service time is B(A — Az). Hence the PGF of the number of customers at the start of vacation is given by (see e.g. [15])
This relation describes the f m transition under the gated discipline. Substituting (9) into (5) results in the governing equation of the system.
The derivative of (9) at z = 1 gives
We define a sequence of functions recursively as
Theorem 3. In the stable M/G/1 multiple working vacation model with gated discipline satisfying assumptions A.1 – A.3 the stationary PGF of the number of customers at the end of a vacation is given as
where $(z) and ^(z) are given as
with
and an empty product is 1.
Proof. Replacing z by f3k(z) in (8) for k > 0 leads to
Solving (17) by recursive substitution for k > 0 yields
It can be shown that for p < 1, which is the condition of stability (see in section 2), limk^TO f3k(z) = 1 for any \z\ < 1 [6]. Using this in (18) yields
By the notations introduced in (13) and (14), (19) can be rewritten as
The unknown term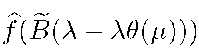 
is obtained by setting 
in (20), therefore is obtained by setting
Substituting (21) into (20) gives the theorem.
Remark
can be also determined by applying (12) in the gated discipline specific
transition (9).
From the definition of
From the definition of
Using these properties we obtain
and from (12) we have
The computation of the second moments is more involved.
and
