A Two-Class Continuous-Time Queueing Model with Dedicated Servers and Global FCFS Service Discipline (Queueing Theory) (Analytical and Stochastic Modeling) Part 2

Comparison of Models and Numerical Examples

In this section, we discuss the results obtained in the previous sections, both from a qualitative perspective and by means of some numerical examples.

In Figures 3 – 6, we compare both systems studied in section 3 and 4 (i.e., the systems with and without global FCFS) through some performance measures. We have also included the performance measures of two extra queueing systems, which can be considered as worst and best cases respectively (or lower and upper bounds). A lower (worst) limit is the well-known M/M/ 1-system, one type of customers and one server with a mean service rate of It is clear that this is indeed a lower performance boundary for our systems. In our systems, always at least one server is working when there are customers in the system. So, they behave at least as good as an M/M/1. A higher performance limit is another well-known queueing system (M/M/2), again one type of customers but two servers with a mean service rate of This is an upper performance boundary for our systems, since in our systems at most two servers are working. So it behaves not better than M/M/2. The solutions of both these queueing systems are standard [18].

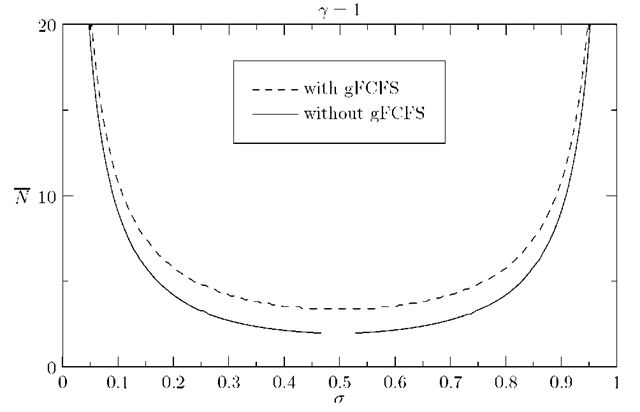
Fig. 3. Mean system occupancy versus parameter 7

Fig. 4. Mean system occupancy versus parameter a for 7 = 1

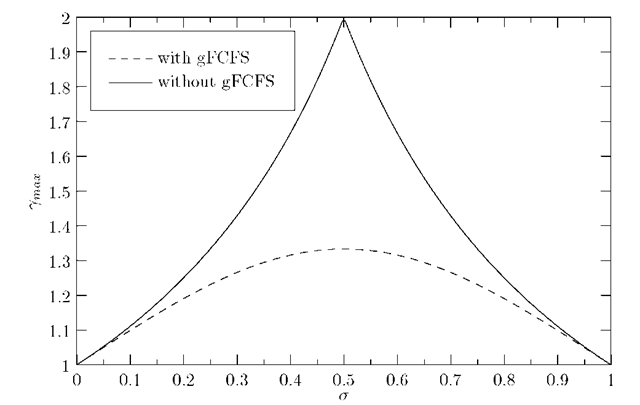
Fig. 5. Ymax, the maximum 7 that still fulfils the stability condition, versus parameter a

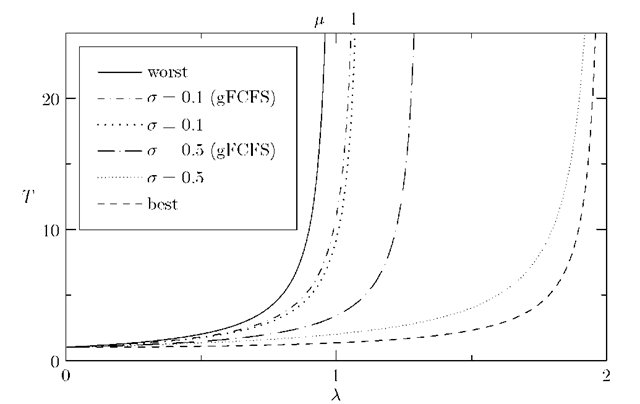
Fig. 6. Mean system delay versus the mean arrival rate and ^ = 1

Fig. 3 shows the mean system occupancy versus parameter 7, for various values of a. For each value of a the mean system occupancy is shown with global FCFS as service discipline (gFCFS) and without global FCFS. It is clear that our system with global FCFS always performs "worse" than the system without this restriction. In the case where the customers are arriving equiprobably (a = 0.5), the impact of global FCFS on the mean system occupancy is not negligible. While the system without global FCFS almost coincides with the upper boundary, the system with global FCFS leans more toward the lower boundary. Intuitively, we might expect at first glance that our system with global FCFS would lie exactly in the middle between the two boundaries, because the probability of a blocking effect is when the next customer is of the same type as the remaining customer in the server which is here always with probability

However, a simple reasoning provides the stability limitIf many customers are present and two servers are working, this lasts until one of the services is finished (on averagetime units). From this instant, one server works with probabilityand two servers work with probability In the first case,this lasts on averagetime units. So, the output rate is on average 1 customer per

Fig. 3 also shows that the difference between the mean system occupancy with and without global FCFS is smaller when there are many customers of the same type (a = 0.1). This can be rather surprising because the probability to have two customers of the same type arriving one after another is much greater in this case and we would expect more blocking compared to the case when our customers are arriving equiprobably. However, the reason why this is not the case, is that the majority of customers are blocked almost all the time by customers of the same type which is in both systems the same. The minority (which is assumed to be much smaller than the majority of customers) who are almost always blocked by customers of a different type, have much less influence on the mean occupancy of the system. So the impact of global FCFS is less pronounced in the mean system occupancy because the impact is mainly on the minority of customers.

In Fig. 4, we have plotted the mean system occupancy versus the parameter a for y =1 (with global FCFS as service discipline and without global FCFS). This figure confirms the observations we made in Fig. 3. We observe again that the difference between the mean system occupancy with and without global FCFS is smaller when there are many customers of the same type. This figure also shows the symmetry of our system (point of symmetry in a = 0.5). The reason for this symmetry, is due to the fact that the mean service rates of the servers are equal. So making server A dedicated to customers of type 2 and server B to customers of type 1 does not have any impact compared to our system. In Fig. 4, we can also see that when customers arrive equiprobably (a = 0.5), an optimum (here minimum) is reached for the mean system occupancy. This is intuitively clear, because in that case the workload of the system is evenly divided between the two servers who have, by assumption, an equal mean service rate j and giving one of the two servers more load has no benefit.

In Fig. 5, Ymax, the maximum 7 that still fulfils the stability condition, is plotted versus a for both studied systems. It is clear that Ymax is always bigger for the system without global FCFS, and this Ymax is determined by the most loaded class. The system with global FCFS also has a largest Ymax for a = 0.5, but the difference with the system without global FCFS is also greatest for this a. Again we can see the symmetry of our system (point of symmetry a = 0.5).

Fig. 6 shows the mean system delay versus the mean arrival rate for a mean service rate ^ of 1 for both studied systems (a = 0.1 and 0.5) and for the two "extrema" systems. Similar conclusions are drawn as for the mean system occupancy.

Conclusions and Future Work

In this paper, we have studied two-class, two-server queues with class-dedicated servers in continuous time assuming a Poisson arrival process where the types of customers are independent. In the first model, we assume a global FCFS service discipline, while in a second model we study the more simple model without a global FCFS service discipline. We have succeeded in deriving an explicit closed-form formula for the pgf of the system occupancy for the system with global FCFS and the pmf (probability mass function) for the system without global FCFS. Comparing these systems has allowed us to uncover the (negative) impact of global FCFS.

The model examined in this paper can be generalized in various directions. First of all, we can study the impact of "class clustering", i.e., customers of any given type may (or may not) have a tendency to "arrive back-to-back". We can intuitively see that this tendency will have a big impact on the blocking effect when operating under a global FCFS service discipline. When they arrive always alternating there will be less blocking than when they alternate only occasionally. This complication will however make the analysis more difficult. A second direction to follow is to let the service times be different for both servers. Finally, we can relax the global FCFS restriction by letting the servers be able to serve one of the m first customers at the front of the queue. We plan to tackle several of these generalizations in future work.