Matrix
In mathematics, a matrix is rectangle group of numbers called elements.The size of the matrix is expressed in the number of rows by the number of columns. In 3D graphics, the most common type of matrix is the 4 by 4 matrix, which contains 16 float values.The XNA Game Studio Matrix structure is a 4 by 4 matrix.A matrix has a number of mathematical applications in a number of fields including calculus and optics. For our purposes, we focus on the use of a matrix in linear algebra because of how useful this becomes in computer graphics.
In computer graphics, the matrix is used to represent linear transformations, which are used to transform vectors. These linear transformations include translation, rotation, scaling, shearing, and projection.The elements of the matrix create their own coordinate spaces by defining the direction of the X,Y, and Z directions along with the translation from the origin. Using a matrix that is 4 by 4 in size enables all of the linear transforms to be combined into a single matrix that is used to transform position and direction vectors.
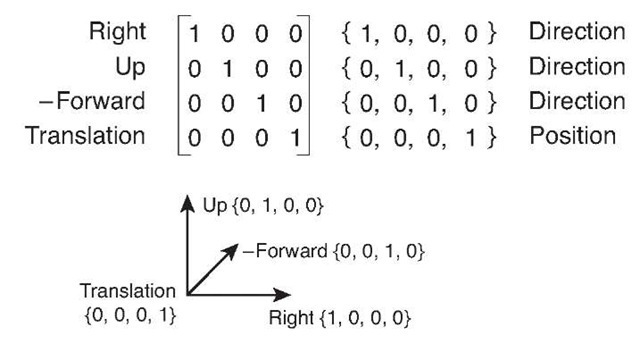
In XNA Game Studio, the matrix structure is row major meaning that the vectors that make up the X,Y, and Z directions and the translation vector are laid out in each row of the matrix. Each row represents a different direction in the coordinate space defined by the matrix.
In the first row, the X vector represents the right vector of the coordinate space. In the second row, the Y vector represents the up vector of the coordinate space. In the third row, the Z vector represents the backward vector of the coordinate space.The forward vector is actually the negation of the Z vector because in a right-handed coordinate space, the Z direction points backwards. The forth row contains the vector to use for the translation of the position. Figure 4.10 shows the vector components of a matrix.
Figure 4.10 Vector components of a matrix
Many of the transforms produce what is called an orthogonal matrix where the X,Y, and Z directions are all 90 degrees from each other. In addition there are some transforms, which contain both orthogonal and normalized direction vectors producing an orthonor-malized matrix.
Identity
The identity matrix, also called the unit matrix, contains elements with the value of one from the top left diagonal down to the bottom right.The rest of the elements in the matrix are all zeros (see Figure 4.11).
Figure 4.11 Identity matrix
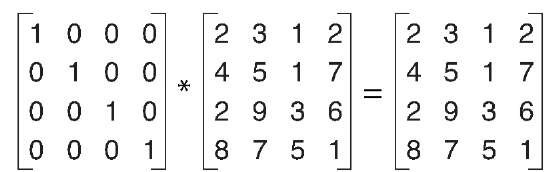
When the identity matrix is multiplied by any other matrix, the result is always the original matrix (see Figure 4.12).
Figure 4.12 Identity matrix multiply
The identity matrix is an orthonormalized matrix that defines the unit directions for X,Y, and Z for the unit coordinate space (see Figure 4.13).
Figure 4.13 Right-handed unit coordinate space
The identity matrix is a base starting point for many of the other types of transforms.
Translation
A translation matrix is a type of matrix that is used to translate or move a vector from one location to another. For example if a vector contains the values { 1, 2, 3 }, a translation of { 2, 1, 0 } moves the vector to { 3, 3, 3 }.
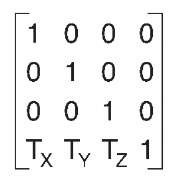
In a translation matrix, the last row contains the values to translate by (see Figure 4.14).
Figure 4.14 Translation matrix
When a vector is multiplied by a translation matrix, the result is a vector with a value equaling the original vector’s value plus the translation of the matrix.
Rotation
A rotation matrix transforms a vector by rotating it. Rotation matrices come in the form of rotations around the X,Y, or Z axes along with rotation around an arbitrary axis. Each type of rotation matrix has its own element layout for defining the rotation. Figures 4.15, 4.16, and 4.17 show the different types of axis rotation matrices.
Figure 4.15 X axis rotation matrix
Figure 4.16 Y axis rotation matrix
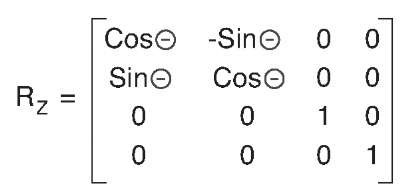
Figure 4.17 Z axis rotation matrix
When a vector is multiplied by a rotation matrix, the resulting vector’s value is equal to the original vector value rotated around the defined axis.
In XNA Game Studio, the creation of rotation matrices is as simple as calling one of the static methods provided by the Matrix structure, such as CreateRotationX.The specified angles are in radian units. In radians, 2 Pi units is equal to 360 degrees. Pi is a mathematical constant, which is the ratio of a circle’s circumference to the diameter of the circle.The value of Pi is around 3.14159.To convert between radians and degrees, use the MathHelper.ToRadians and MathHelper.ToDegrees methods.
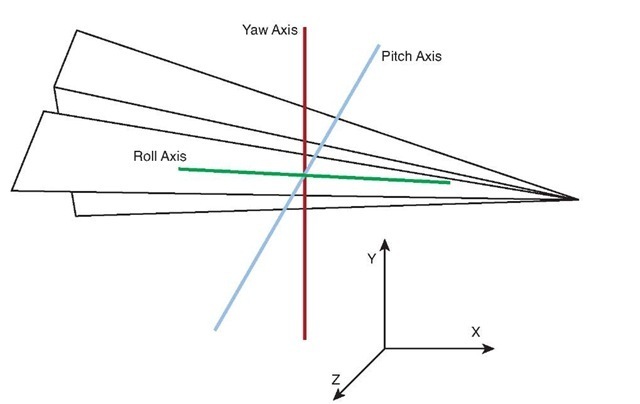
Rotations are sometimes referred to in terms of yaw, pitch, and roll.These represent rotations around the current coordinate spaces right, up, and forward vectors, which are not necessarily the same as the unit X,Y, and Z axes. For example, if an object is already rotated 45 degrees around the Y axis, the forward vector is not in the negative Z direction anymore. It is now halfway between negative Z and negative X (see Figure 4.18).
Figure 4.18 Yaw, pitch, and roll vectors for an oriented object
Rotating this object around the X axis is not the same as rotating around the pitch vector, because the pitch vector no longer is equal to the unit X vector.
Scale
A scale matrix transforms a vector by scaling the components of the vector. Like the identity matrix, the scale matrix uses only the elements in the diagonal direction from top left to lower right.The rest of the elements are all zeros (see Figure 4.19).
Figure 4.19 Scale matrix
When a vector is multiplied by a scale matrix, each component in the vector is scaled by a corresponding element in the matrix. A scale matrix does not have to be uniform in all directions. Nonuniform scale is also possible where some axis directions are scaled more or less than others.
Combining Matrix Transforms
Matrices cannot only be multiplied with vectors to transform them, but can also be combined together to form a new linear transform. The resulting matrix can then be used to transform the vector. The combined transforms on the vector have the same effect as multiplying each against the vector in succession.
Multiple matrices are combined to create a complex transform that is finally multiplied with the vector.This is beneficial when you are transforming thousands of vectors that represent the vertices of triangles in geometry. The resulting combined matrix needs to be calculated only once and can be used for all of the geometry.
When multiplying two matrices A by B, the number of columns in the first matrix A has to equal the number of rows in matrix B. In XNA Game Studio, this is not a concern because the Matrix structure is 4 by 4 square.
Note
When multiplying a vector with a matrix, the vector is treated as a 1 by 4 matrix.
Matrix multiplication is not commutative meaning that A X B is not the same as B X A, which makes sense if you think about it geometrically. If you have a rotation matrix R and multiply it by a translation matrix T, the resulting matrix first rotates an object and then translates the object. If you reverse the order, the object first translates and then rotates causing the object to orbit.The order you combine matrices is important. In general, you want to first scale, then rotate, and finally translate (see Figure 4.20).
Figure 4.20 Results of multiplying by rotation and translation matrices in both orders
Manipulating Vectors with Matrices
Matrices are useful in transforming vectors. As we have discussed, vectors can be used for position data for things like the position of triangles that make up geometry in the game or they can be used for directions for things like the direction and velocity a car is mov-ing.Transforming these two types of vectors occurs slightly differently and has to do with the fourth component of the vector, the homogeneous W component.
As we discussed, 4 by 4 matrices are used because they have the capability to hold multiple types of linear transforms in a single matrix.To be able to multiply a vector by a matrix, the number of components of the vector must equal the number of rows of the matrix.The fourth row of the matrix holds the translation of the matrix.
For vectors that represent position, it is important that the translation of the matrix affects the vector that is multiplied. Because of this, the W component of vectors that represent positions should have a value of 1. This enables the matrix multiply to include the affect of the translation elements of the matrix.
For vectors that represent a direction and magnitude, they should not be translated when multiplied by a matrix. Because of this, the W component of the vectors that represent direction vectors should have a value of 0.This enables the matrix multiply to not allow the translation of the matrix to affect the vector.
Often in your game, you will not want to store your position and direction vectors as Vector4 types. Storing these values as a Vector3 saves you the memory of an extra float component. It also saves you the trouble of having to set the W component.To determine whether the vector is used for position or as a direction, the Vector3 structure provides two transform methods.The first called Transfrom takes a matrix and expects the input value to be a position vector. It expands the Vector3 into a Vector4, sets the W component to 1, and then multiplies the input vector by the matrix returning the resulting vector as a Vector3 after dropping the added W component.The other method TransformNormal works in the same way except it expects a direction vector and sets the W component to 0.Tables 4.4, 4.5, and 4.6 contain the fields, properties, and methods of the Matrix type.
Table 4.4 Fields of Matrix
|
Field |
Type |
Description |
|
M11 |
float |
Element in the first row and first column |
|
M12 |
float |
Element in the first row and second column |
|
M13 |
float |
Element in the first row and third column |
|
M14 |
float |
Element in the first row and fourth column |
|
M21 |
float |
Element in the second row and first column |
|
M22 |
float |
Element in the second row and second column |
|
M23 |
float |
Element in the second row and third column |
|
M24 |
float |
Element in the second row and fourth column |
Table 4.4 Fields of Matrix
|
Field |
Type |
Description |
|
M31 |
float |
Element in the third row and first column |
|
M32 |
float |
Element in the third row and second column |
|
M33 |
float |
Element in the third row and third column |
|
M34 |
float |
Element in the third row and fourth column |
|
M41 |
float |
Element in the fourth row and first column |
|
M42 |
float |
Element in the fourth row and second column |
|
M43 |
float |
Element in the fourth row and third column |
|
M44 |
float |
Element in the fourth row and fourth column |
Table 4.5 Properties of Matrix
|
Property |
Type |
Description |
|
Identity |
Matrix |
Returns an identity matrix |
|
Right |
Vector3 |
Returns the right vector of the matrix |
|
Left |
Vector3 |
Returns the left vector of the matrix |
|
Up |
Vector3 |
Returns the up vector of the matrix |
|
Down |
Vector3 |
Returns the down vector of the matrix |
|
Forward |
Vector3 |
Returns the forward vector of the matrix |
|
Backward |
Vector3 |
Returns the backward vector of the matrix |
|
Translation |
Vector3 |
Returns the translation vector of the matrix |
Table 4.6 Abbreviated Table of Matrix Methods
|
Method |
Description |
|
CreateTranslation |
Returns a translation matrix from a given translation vector |
|
CreateRotationX |
Returns a rotation matrix around the X axis in the given amount |
|
CreateRotationY |
Returns a rotation matrix around the Y axis in the given amount |
|
CreateRotationZ |
Returns a rotation matrix around the Z axis in the given amount |
|
CreateFromAxisAngle |
Returns a rotation matrix around the given axis in the given amount |
|
CreateFromYawPitchRoll |
Returns a rotation matrix from the given yaw, pitch, and roll amounts |
Table 4.6 Abbreviated Table of Matrix Methods
|
Method |
Description |
|
CreateScale |
Returns a rotation matrix from the given scale |
|
Multiply |
Returns the result of multiplying two matrices together |