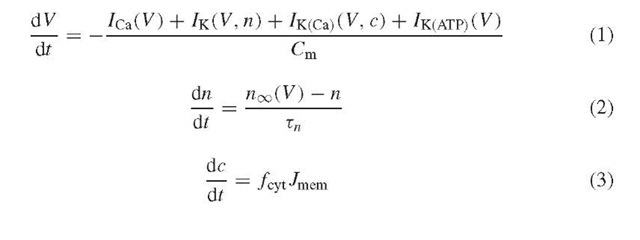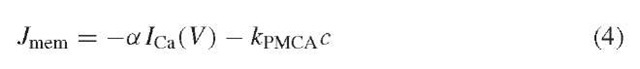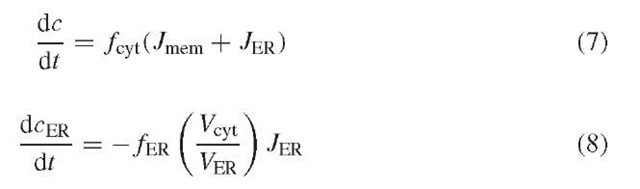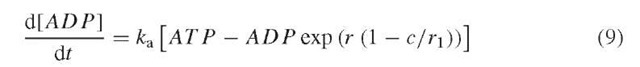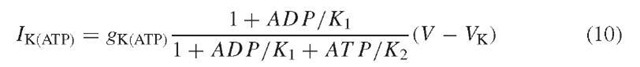1. Introduction
Mammalian metabolism is well adapted to switch between carbohydrate and lipid fuels depending on availability. One of the key hormones involved is insulin, which promotes glucose oxidation and fat storage when carbohydrate is abundant. In the developed world, unprecedented affluence has resulted in chronic excess of both nutrients relative to energy expenditure requirements, leading to an epidemic of obesity, hypertension, hyperlipidemia, and heart disease. An integral part of this metabolic syndrome is resistance to the effects of insulin, possibly as a compensation for overnutrition (Unger, 2003). In response, the p-cells of the pancreatic islets of Langerhans oversecrete insulin to maintain plasma glucose within normal ranges. In many cases (currently about 6% of the population of the United States), the p-cells fail to compensate, leading to hyperglycemia (Type II diabetes), further morbidity, and premature death. For these reasons, there has been much interest in understanding how p -cells regulate plasma glucose. This control mechanism centers on complex patterns of oscillation in membrane potential and cytosolic calcium, which are difficult to understand without the aid of mathematical models. Those models are the focus of this review.
2. Schematic model
The p-cell models build on the Hodgkin-Huxley paradigm (Hodgkin and Huxley, 1952), in which the plasma membrane is represented as an RC circuit, with the ion channels providing the resistance and the lipid bilayer providing the capacitance. The great success of such models in explaining the diverse electrical properties of neurons, muscle, and endocrine cells stems from the ability to reduce the electrical apparatus to a simple physical model, which can be represented by a small system of ordinary differential equations. The availability of dynamic readouts (voltage and calcium) with high time resolution has also been crucial. The validity of isolating the electrical module was strikingly demonstrated by transfecting voltage-dependent Na+ and K+ channels into nonexcitable Chinese hamster ovary cells, which endowed them with neuron-like action potentials (Hsu et al., 1993).
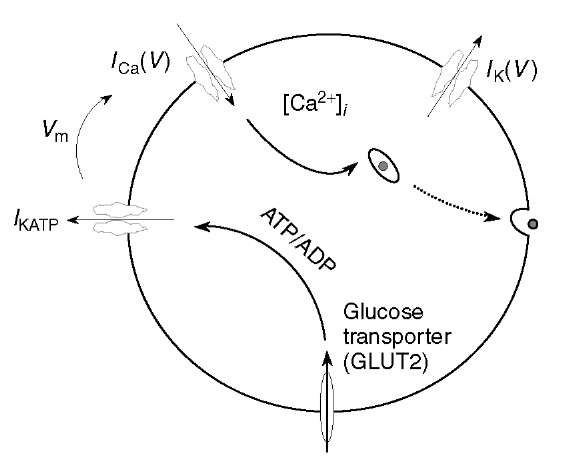
Figure 1 Consensus schematic of ft-cell. Glucose triggers depolarization and Ca2+ entry, which signals exocytosis of insulin granules
The minimal parts list for the ft -cell is shown in Figure 1. The voltage-dependent Ca2+ channel conducts Ca2+ ions into the cell, which raises the transmembrane voltage, V, whereas the K+ channel gates efflux of K+ and restores V to a low level. The temporal interaction of the two channels is sufficient to explain the repetitive spiking observed in ft-cells. The Ca2+ influx also provides the primary chemical signal to trigger exocytosis of insulin-containing granules. These components are typical of many endocrine cells, but the ft -cell needs an additional metabolic module to connect the level of electrical activity to plasma glucose concentration. Metabolism of glucose raises the ratio of ATP to ADP, which closes a third channel, the K(ATP) channel. Thus, in the absence of glucose, ft-cells are electrically silent, but they generate Ca2+-dependent action potentials when glucose is elevated.
This is the consensus schematic model for ft-cells and is sufficient for understanding many aspects of diabetes pathology and therapy. For example, one of the classes of drugs used to treat Type II diabetes, the sulfonylureas, block K(ATP) channels independent of glucose metabolism and augment insulin secretion (Ashcroft and Rorsman, 1989). Also, recently it has been shown that either a surplus or a deficit of K(ATP) activity can lead to diabetes (Seino and Miki, 2003). In the former case, K(ATP) channels that fail to close in response to glucose result in inadequate secretion of insulin. In the latter case, K(ATP) channels that are always closed independent of glucose result in childhood hyperinsulinism. Some patients who survive this devastating hypoglycemia into adulthood become diabetic, possibly because their ft-cells fail from chronic depolarization and exposure to high [Ca2+] (Glaser, 2003).
In both mice (Ashcroft and Rorsman, 1989) and humans (Martin and Soria, 1996), insulin secretion is controlled by oscillations of calcium, which are driven by bursts of action potentials with periods ranging from tens of seconds to several minutes (see Figure 2 for an illustration using the model). We want to understand how bursting arises, how it is modulated by glucose and other signals, and how such a broad dynamic range is achieved. Three illustrative models are presented below in a didactic sequence of increasing complexity and explanatory power. Bear in mind that the actual historical development was more complex and subject to alternate interpretations.
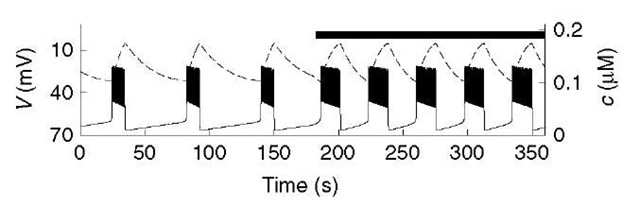
Figure 2 Simulation of glucose step with Chay-Keizer-like model (equations 1-5). Each plateau in voltage (V; solid) is a train of brief spikes. Cytosolic calcium (c; dashed) rises slowly to terminate the bursts and recovers slowly in the silent phase. The black bar indicates period of elevated glucose
3. The Chay-Keizer model
The first widely adopted mathematical model for bursting in p-cells was developed by Chay and Keizer (1983), on the basis of the hypothesis of Atwater and Rojas that the slow dynamics of intracellular free Ca2+ are responsible for packaging impulses into bursts (Atwater et al., 1980); that is, the sustained high voltage of the active phase of each burst would slowly increase cytosolic [Ca2+] (c), which would gradually activate a Ca2+-activated K+ (K(Ca)) channel until a critical level was reached that would shut the spiking off. In the absence of spiking, c would slowly recover, giving a long silent phase (Figure 2).
Chay and Keizer also sought to explain how an increase in plasma glucose modulates the bursts by prolonging the active phases and shortening the silent phases, that is, increasing the plateau fraction. They suggested that increased glucose would increase activity of the plasma membrane Ca2+-ATPase (PMCA), slowing the rise of c and accelerating its fall. In keeping with the modular approach, the machinery of metabolism enters only through its effect on the pump rate (black bar, Figure 2).
The equations that correspond to the above scheme and that were used to produce Figure 2 are in outline:
(The full equations and parameter values are posted at http://mrb.niddk.nih.gov/sherman.) The electric circuit is represented by equations (1) and (2) for the membrane potential (V ) and the activation level (open probability) of the voltage-dependent K+ current (n), respectively. Equation 1 is Kirchhoff’s law, which balances capacitive current with the four ionic currents, the voltage-dependent Ca2+ (ICa), voltage-dependent K+ (IK), Ca2+-dependent K+ (IK(Ca)), and ATP-sensitive K+ (IK(ATp)) currents. Note that in order to obtain spikes, the RC circuit must be elaborated by assuming that the resistive elements (i.e., the ion channels) change their conducting state in response to V . These changes have been measured (Ashcroft and Rorsman, 1989) and incorporated semiquantitatively into the model. For the present, the conductance of IK(ATp) is held constant, unlike the conductances of the other currents, which vary as V or c change in time. Later, we will introduce dependence on glucose through the ATp production rate.
The slow dynamics of c are modeled by simple mass balance, assuming one well-mixed compartment. Influx through Ca2+ channels increases c, while efflux through the pMCA decreases it:
(Note that ICa is negative by convention, so – aICa is positive.) The net flux of Ca2+, Jmem, is multiplied by f cyt, the ratio of free to total (free + buffered) Ca2+ . f cyt is small here (0.00025), which makes c slow. Calcium responds to the membrane potential through ICa, and in turn influences the membrane potential through IK(Ca) = gK(Ca)«(V – VK), where the activation variable m is:
A noteworthy feature of the Chay-Keizer model is that the voltage plateau is not explicitly included in the model. It is an emergent property arising from the V – n interactions. This contrasts with an earlier model (Matthews and O’Connor, 1979), which postulated a special plateau current. This made for a more complex and cumbersome model than Chay-Keizer and may have contributed to its later neglect, in spite of its anticipation of many aspects of Chay-Keizer and other later models.
4. The endoplasmic reticulum: A second Ca2+ compartment
In addition to accounting for two major known properties of ft-cells, the Chay-Keizer model made a prediction that cytosolic Ca2+ would oscillate, with a slow rise and fall. When Ca2+ was later imaged in ft-cells (Valdeolmillos et al., 1989), it was indeed seen to rise and fall, which was not surprising, but the kinetics were not as expected: c rose rapidly at the beginning of the active phase to a plateau and sometimes even fell slightly toward the end of the active phase. The K(Ca) channel hypothesis fell into disfavor, but has been revived, in part because of the discovery of a candidate K(Ca) channel in p-cells (Goforth etal., 2002; Gopel et al., 1999), and in part because of an improved model due to Chay (1996), which included a second, internal Ca2+ compartment, representing the endoplasmic reticulum (ER).
There are several reasons for including the ER. As a storehouse for Ca2+, it can influence the Ca2+ dynamics of both excitable and nonexcitable cells (Berridge, 1997). In islets in particular, releasing Ca2+ from the ER by either blockade of the ER Ca2+ pump (SERCA) or activation of IP3 receptors dramatically affects electrical activity, Ca2+ oscillations, and secretion (Bertram et al., 1995b; Goforth et al., 2002; Worley et al., 1994).
The ER compartment is incorporated into the model by adding an ER-to-cytosol flux term (JER) to equation (3) and by adding a differential equation for the free ER Ca2+ concentration (cER). All forms of efflux are subsumed in a leakage pathway (Jleak), and influx occurs through SERCA pumps (JSERCA):
We neglect the known nonlinearities of these processes and write /leak = pleak(cER – c) and /SERCA = kSERCAc. The effect of IP3 can be represented simply by an increase in pleak. The equations for c and cER are
where f ER is the ER Ca2+ buffering factor, and Vcyt and V ER are the cytosolic and ER volumes.
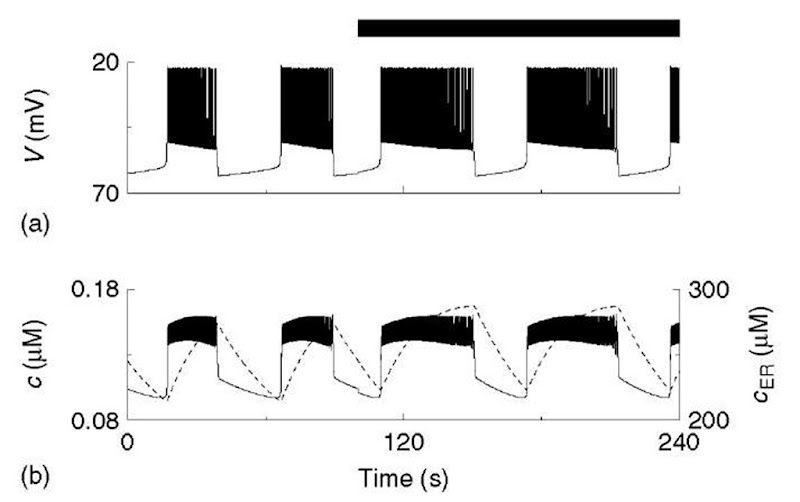
The behavior of the enhanced model is shown in Figure 3. The rapid jump in c at the beginning of each active phase reflects the intrinsic kinetics of cytosolic Ca2+, which have been accelerated compared to Figure 2 by reducing the cytosolic buffer capacity (i.e., increasing f cyt to the more realistic value of 0.01). This rise in c does not alone provide adequate inhibition to terminate the active phase, but as the ER slowly fills, c is pushed up to the necessary critical level. When spiking ceases, c jumps down rapidly and then slowly decays as the ER gives back the Ca2+ it took in during the active phase. Thus, like a buffer, the ER slows down c, but because the ER is slow (whereas buffers are fast), c displays two distinct kinetic phases, in agreement with experiments.
The model parameters in Figure 3 are chosen to give an oscillation period comparable to that typically observed in islets (10-60 s). However, if gK(Ca) is increased, the initial jump in c becomes sufficient to terminate an active phase without assistance from cER, resulting in a period of only a few seconds. (Similar fast bursting can also be obtained by partially emptying the ER. See Figure 4.) Conversely, reducing gK(Ca) (and possibly adjusting kPMCA), produces periods of several minutes, which are also observed in experiments. This broad range of frequencies is possible because the time scale of oscillations is determined by this “phantom bursting” because the time scale is not determined by any single process (Bertram and Sherman, 2004).
Figure 3 Chay-Keizer model with a slow ER compartment (cER, dashed). c now has fast and slow components, and increasing pMCA rate now increases both plateau fraction and mean c
A comparison of Figures 2 and 3 shows that the ER enhances the model in another way. Whereas both the original Chay-Keizer model and the ER model explain how glucose can raise plateau fraction, in the one-compartment Chay-Keizer model, this does not lead to an increase in the mean level of cytosolic [Ca2+]. In the ER model, in contrast, the approximately square shape of c means that an increase in plateau fraction produces an increase in the average level of c, without any change in the minimum and maximum values, as more time is spent at the higher level relative to the lower level. Note that this occurs in spite of the fact that the rate of pumping Ca2+ out of the cell is increased, illustrating that steady state intuitions may not apply when there are oscillations.
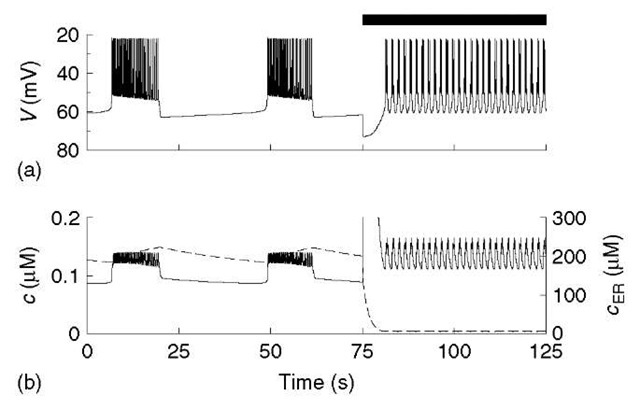
Figure 4 Response of model with ER to acetylcholine (ACh), modeled as a step increase in pleak, throughout period denoted by black bar. Release of Ca2+ from ER (b; dashed) gives a transient sharp peak of c (solid; truncated for clarity). Plateau of high c is maintained by an ACh-activated inward current, which drives depolarized, fast bursting (a)
As alluded to earlier, inclusion of the ER also allows the model to account for the effects of acetylcholine (ACh) application (Figure 4). In vivo, ACh is released from parasympathetic nerve terminals in the pancreas to stimulate the islets in response to food ingestion (Woods and Porte, 1974). This auxiliary control mechanism raises insulin in anticipation of the coming glucose load and helps limit the rise in plasma glucose. At the cell level, ACh stimulates the production of IP3, which activates IP3 receptors on the ER. Here we again collapse an external regulatory module into a change in a parameter of the core electrical/calcium module: the efflux permeability p leak is stepped up 45-fold. This is sufficient to produce the increase in burst frequency seen experimentally. However, in order to capture the rise in V and c that are also seen, we need to add a small depolarizing current (/ACh = gACh(V – VACh), where gACh = 5 pS and VACh = 0) to the V equation. Such a current has now been found (Mears and Zimliki, 2004; Rolland etal., 2002). The depolarized bursting and elevation of the cytosolic Ca2+ concentration are critical because they contribute to the increase in insulin secretion.
5. Oscillations in glucose metabolism
We now consider the glucose dependence of the K(ATP) channel. If the K(ATP) conductance is assumed to decrease with external glucose concentration, then plateau fraction is modulated similarly to the changes obtained in Figures 1 and 2 by varying PMCA pump rate (not shown). Beyond this, there is some evidence that ATP and ADP concentrations in p-cells vary over time (Ainscow and Rutter, 2002) in a Ca2+-dependent manner (Kennedy et al., 2002). This was proposed by Keizer and Magnus (1989), who assumed that the rate of ATP production decreases when cytosolic Ca2+ inhibits the mitochondrial membrane potential. Phenomenologically, this can be represented by the following equation for ADP concentration:
We assume that the total nucleotide concentration, ADP + ATP, is constant, so no differential equation is needed for ATP. The effect of ATP to block the K(ATP) conductance is antagonized by ADP by competitive inhibition:
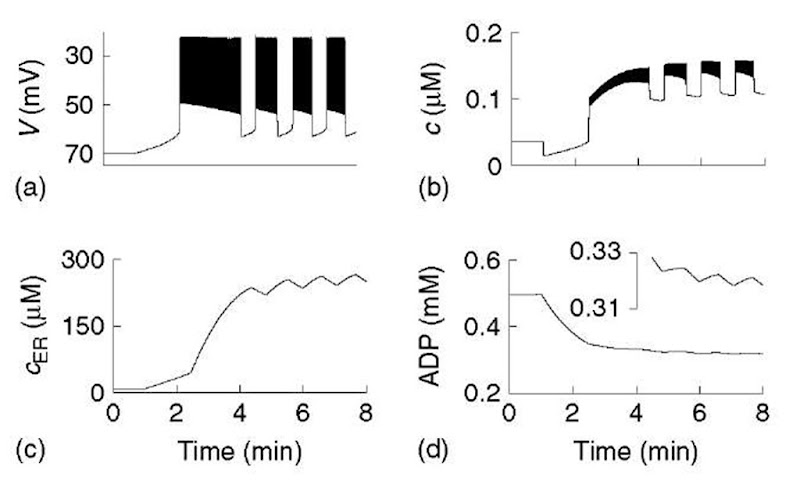
The net result is that a rise in c results in a slow (minutes) rise in ADP and an increase in IK(ATP). An increase in glucose can now be represented by an increase in the parameter r in equation 9 in combination with changes in pump rates. We illustrate this in Figure 5 for the situation where glucose is raised from a subthresh-old level to a level that permits bursting. Low glucose is simulated by reducing r and SERCA pump rate, kSERCA, which drains the ER and elevates ADP. Starting in that condition, we assume that when glucose is raised, kSERCA increases rapidly, producing a transient drop in c (Figure (5)b). Over several minutes, ADP declines, reducing K(ATP) conductance, and V gradually increases. When the voltage threshold for activation of ICa is reached, V jumps up sharply and spiking begins. The ER, however, is still depleted and acts as a sink for Ca2+. This limits activation of the K(Ca) conductance, resulting in a prolonged period of spiking. After several more minutes, the ER is filled, and bursting can begin. ADP oscillates during the bursting phase (inset, Figure (5)d) and combines with c to drive the bursting. Thus, with inclusion of dynamics for ADP, the model is able to account for the complex triphasic transient of electrical and cytosolic Ca2+ activity observed experimentally (Bertram et al., 1995b; Goforth et al., 2002; Worley et al., 1994).
Figure 5 Model with ER and calcium feedback on nucleotide dynamics. Glucose is stepped at T = 1 min, initiating a triphasic transient (see text). In the steady state, ADP oscillates as well as cytosolic and ER calcium
The incorporation of two very slow processes, cER and ADP, makes the model more robust and endows it with some redundancy. This may help account for the observations that oscillations can persist when the ER is disabled by blocking SERCA (Fridlyand et al., 2003) (K(ATP) can compensate for the loss of K(Ca)) or when K(ATP) channels are blocked by sulfonylureas (Rosario et al., 1993) (K(Ca) can compensate for the loss of K(ATP)). (See also Bertram and Sherman, 2004.) A third slow process recently proposed by Fridlyand et al. (2003), Na+ accumulation that activates the Na+ pump, might also be helpful to explain this complex phenomenology.
6. Summary and prospects
We have traced in outline the evolution of the Chay-Keizer family of models over 20 years. The first models explained bursting of membrane potential and modulation of plateau fraction by glucose. They also predicted oscillations of cytosolic Ca2+, which were later seen, but with a different kinetic character. This led to a second wave of models with more accurate Ca2+ kinetics, and predictions of oscillations in ER Ca2+. The latter have not yet been demonstrated experimentally, and indeed their existence has been challenged on the basis of ER measurements in permeabilized cells (Tengholm etal., 2001). Measurements of ER Ca2+ in intact cells undergoing cytosolic Ca2+ oscillations are needed to test this prediction.
The current generation of models can account for the full range of observed oscillation periods, spanning 2 orders of magnitude, from seconds to minutes. They also account for modulation of electrical activity (and, implicitly, insulin secretion) by cholinergic stimuli as well as glucose (Figure 4), and the complex transients seen when glucose is first elevated (Figure 5). The initial prolonged spiking phase may be related to the early large peak of insulin secretion, which is lost in Type II diabetes (Kahn, 2001). However, a serious treatment of secretion will require consideration of the dynamics of vesicle exocytosis and recycling (Rorsman and Renstrom, 2003) in response to both local (submembrane) and bulk cytosolic Ca2+ and also to non-Ca2+ signals.
Future models will need to address other modulators, such as glucagon-like peptide, which potentiates secretion by elevating cAMP, and epinephrine, which blocks secretion and slows down oscillations. The former pathway is a drug target of great current interest because, unlike K(ATP) channel blockade, it is only effective when glucose is elevated, eliminating the danger of therapy-induced hypoglycemia. Recent data indicate that insulin may have both stimulatory and inhibitory effects on its own secretion (Khan et al., 2001). This is an unsettled area that merits further investigation both experimentally and theoretically.
We have included metabolic oscillations based on Ca2+-dependent effects in the mitochondria (Figure 5). However, there is also some evidence for glycolytic oscillations (Tornheim, 1997). One possible role of glycolytic oscillations is in explaining the packaging of the bursts themselves into higher-order patterns, or “bursts of bursts” (Wierschem and Bertram, 2004), and other roles are currently under investigation.
For brevity, we have described here only models for a single cell, representing an electrically synchronized islet. For an overview of models that explicitly treat the nonobvious effects of electrical coupling, see Sherman (1996).
Thanks to judicious pruning of unnecessary detail, the current models are similar in complexity to the original Chay-Keizer model, in spite of their greater explanatory power. The use of simple models has paid dividends in terms of insight and mathematical analysis that goes beyond mere simulation. Of particular note is the establishment of a general classification scheme for burst mechanisms (Bertram et al., 1995a). This has not only enhanced our understanding of the p-cell models but also situated them in a general perspective of bursting models for neurons and other secretory cells.
The p-cell has provided an interesting case study of the interaction of physiology and modeling with genomic methods. For example, the K(ATP) channel was identified by physiological experiments, and its possible roles, as either a passive modulator or active participant in oscillations, have been clarified by modeling. In parallel, sequencing has suggested how its structure underlies its function, and genetic scans have uncovered connections to disease (hyperinsulinism and Type II diabetes). Yet, we do not yet know why, according to limited data, in rats glucose appears not to modulate plateau fraction, but rather gross depolarization (Antunes etal., 2000), similarly to ACh in mice (Figure 4). The islet a-cells in both species also possess K(ATP) channels, but their response is just the reverse of ft -cells – electrical activity and secretion are inhibited by glucose. How such different behaviors can arise in cell types that differ in rather subtle and quantitative ways poses a challenge for future studies integrating all the techniques at our disposal.