The Hough transform is a tool to detect and quantify shape primitives in images, particularly in the presence of noise. The Hough transform is a robust tool to extract features (such as straight edges, circles, or ellipses, but also primitives defined by polygons) from images and describe them parametrically. The Hough transform is generally used as one step in a processing chain. First, the image needs to be segmented such that the edge of the shape of interest becomes a prominent feature. Following segmentation, the Hough transform serves as a filter for primitives. With the Hough transform, geometric primitives can be detected and separated from image noise. Implicitly, the primitives can be quantified (e.g., circle radius and position). The strength of the Hough transform to find, extract, and quantify shapes lies in the ability to identify those shapes and features even if the outline is broken, incomplete, or corrupted by noise in the thresholded image.
The original Hough transform, developed by Paul Hough in 1962,10 was designed to identify straight lines in images. In 1972 the Hough transform was refined by R. Duda and P. Hart,4 who introduced the line representation in polar coordinates and proposed an extension toward ellipses. A further milestone was the generalization by D. H. Ballard,2 who not only presented a generalization for analytic curves but also proposed the use of shape templates (see also Merlin and Faber15 for an alternative generalization).
The idea behind the Hough transform is to transform the shape of interest into its parameter space. For example, a line in a Cartesian (x,y) coordinate system can be described by the equation
with the constants m (the slope of the line) and n (the y intercept). Each line is uniquely characterized by the pair of constants m and n. Therefore, any line can be represented by a point in a coordinate system of m and n. Conversely, any point (x,y) is associated with a set of values for m and n that satisfy Equation (7.1), which can be rewritten as
which, for constant x and y, is another line equation in a (m,n) coordinate system. Therefore, each point (x,y) is represented by a line in (m,n)-space. It can be seen from Equation (7.2) that the line equation (7.1) is unsuitable, since values in (m,n)-space become undefined for vertical lines. In the next section, a different line equation will be presented, but the principle of the Hough transform can best be explained with the basic equation (7.1).
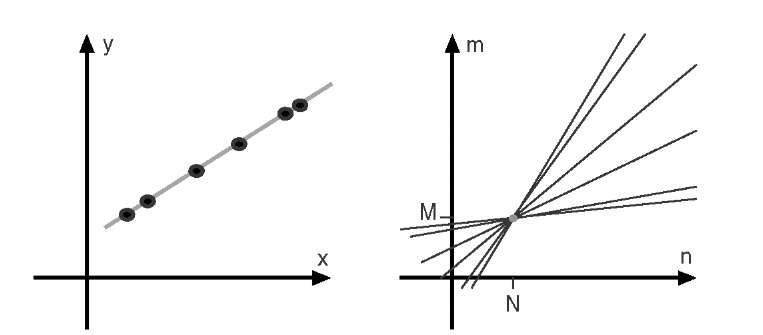
When a set of points (yk,xk) that lie on a line described by y = Mx + N is transformed into (m,n)-space (called Hough space or parameter space), each point is represented by a line in Hough space:
All lines meet in one point (M,N), as shown in Figure 7.1. To extract the feature (in this section, the line), a second step is necessary. In Figure 7.1, only six points of the gray line are examined. Each point is now transformed into Hough space, and the traces of the resulting lines are accumulated. Starting with an empty image matrix (i.e., all elements are zero) in Hough space, the lines that correspond to each point are traced, and the image values along the trace are incremented by 1. This process is often described as the point (yk,xk) casting a vote in Hough space, and the process of accumulating votes is common to all varieties of Hough transforms. In the process, the Hough-space pixel at (M,N) is incremented for each line and therefore accumulates the most votes. Peak detection would now provide a single point, (M,N), and the reconstructed equation for the line is y = Mx + N.
FIGURE 7.1 Principle of the Hough transform. Individual points in (x,y)-space are represented by lines in Hough space. If all points lie on a line y = Mx + N, all lines in Hough space will meet at point (M,N).