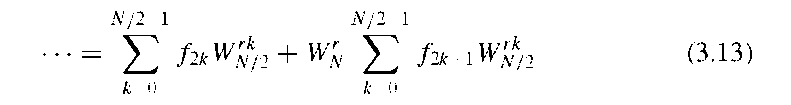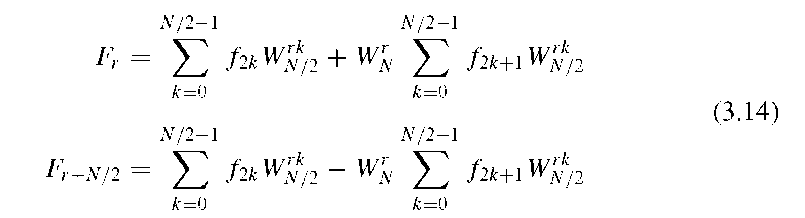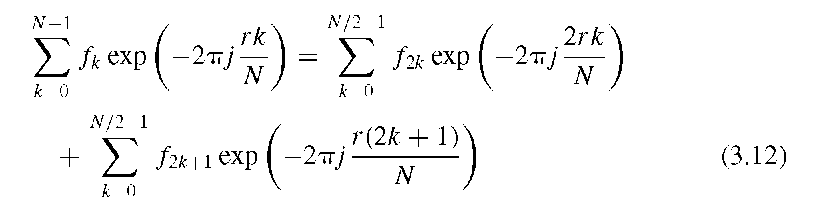Abrupt changes of image intensity, such as lines or edges, have many frequency components. The Fourier transform of a step (such as the transition from 1 to 0) exhibits a broad spectrum with a (sin w)/w characteristic. If the intensity change is more gradual, its frequency components drop off more rapidly toward higher frequencies. Figure 3.5 demonstrates this effect. The Fourier transform of a white square (i.e., a step change of intensity in both the x and y directions) shows predominantly frequency components along the u and v axes (Figure 3.5A and B). A more gradual transition from black to white as in Figure 3.5C exhibits a much more rapid decay of the frequency components toward higher frequencies (Figure 3.5D). In the extreme, the gradual intensity change is sinusoidal (Figure 3.3A) and associated with a very narrow frequency peak. Notably, the Fourier transform of random pixel data (noise) also has a broad frequency spectrum. In other words, the spectral power of noise is spread over the entire frequency spectrum.
FIGURE 3.5 Frequency spectrum of abrupt intensity changes. A white square (step intensity changes in the x and y directions, A) has frequency components widely distributed along the u and v axes (B; shown is the logarithmic magnitude for better visualization). The more gradual, Gaussian-shaped transition (C) has frequency components that taper off much more rapidly toward higher frequencies (D).
FIGURE 3.6 If an image is rotated, such as the white square from Figure 3.5A that is rotated clockwise by 30° in image A, its Fourier spectrum is that of the original image, but also rotated by the same angle (B).
If an image is rotated by a certain angle, the frequency spectrum of the rotated image is identical to the frequency spectrum of the original image but also rotated by the same angle (Figure 3.6). This is a consequence of the linearity of the Fourier transform, one of its most fundamental properties. In this context, linearity means that (1) a scaled image has a Fourier transform scaled by the same value, and (2) the Fourier transform of two images, added together pixel by pixel, is identical to the addition of the Fourier transforms of the individual images:
where F denotes the Fourier transform; I, I1, and I2 are images; and a is a scalar.
The Fourier transform exhibits a number of symmetry properties. Generally, these are more important in one-dimensional data sets than in images, since images rarely exhibit relevant symmetries. If the original data are real valued, an even function [f (t) = f (-1)] produces a real-valued, even Fourier transform, whereas an odd function (f(t) = -f(-1)]) produces an imaginary, odd Fourier transform. Any asymmetrical function yields a complex Fourier transform. However, the Fourier transform always exhibits Hermitian symmetry, that is, F(w) = F*(-w), where F* is the complex conjugate of F. In two dimensions, the Hermitian symmetry can be expressed as F(u,v) = F*(-u,-v).
Fast Fourier Transform The discrete Fourier transform (DFT) in Equation (3.9) can be implemented in a straightforward manner. Because of the double summation needed for every point of F(u,v), the computational effort increases with the fourth power of the image size, specifically M2N2, if the image is M x N pixels in size. The extreme popularity of the Fourier transform can be explained primarily by the development of the fast Fourier transform (FFT). In one dimension the FFT reduces the computational effort from N2 for the conventional discrete Fourier transform to N log2N for the FFT. To illustrate the efficiency gain, assume that a two-dimensional fast Fourier transform of a 1024 x 1024 pixel image takes 5 seconds on a personal computer. The conventional discrete Fourier transform would take 14 hours for the same image. It is easy to imagine how important this efficiency gain was in the early days of the digital computer, when computing power was only a fraction of what today’s computers are capable of. This was the time when Danielson and Lanczos8 created an artful recursive implementation of the DFT using the symmetries of the complex exponentials. The Danielson-Lanczos approach was refined further by Cooley and Tukey,7 and the Cooley-Tukey algorithm is the basis of almost all FFT implementations today. The history of the discovery of fast Fourier algorithms is quite interesting, and a review paper by Cooley et al.6 provides a historical outline. Additional aspects, particularly the impact of the FFT on research and science, as well as some speculation into future developments, are presented by Rockmore.27
In the second summation term, a constant phase factor of![]() appears, and the definition of a phase shift
appears, and the definition of a phase shift![]() allows us to simplify Equation (3.12):
allows us to simplify Equation (3.12):
It can be seen from Equation (3.13) that the N-point DFT reduces to two N/2-point DFTs. The symmetry of the phase shifts comes into play when the number of summations for r is reduced from N to N/2 by using the following two equations for the lower and upper halves of the DFT:
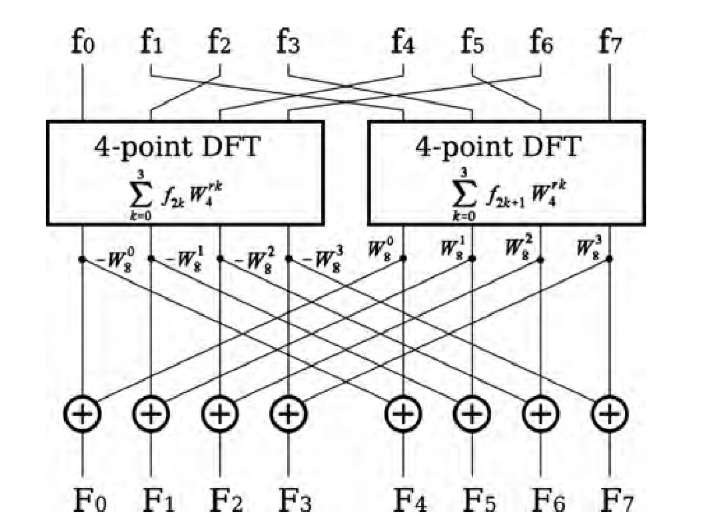
The upper and lower half-DFTs are identical, with the exception of the sign of the phase shift. This reduction of a N-point DFT into two N/2-point DFTs and some multiplications and additions is illustrated in the signal-flow graph in Figure 3.7.
In the same fashion, the two DFTs of N/2 points can be subdivided into four DFTs of N/4 points, and so on, until only two-point DFT operations remain. These operations are called butterfly operations and constitute the fundamental operation of the FFT. The phase shift WrN is often called a twiddle factor, and this factor differs only in the sign between the lower and upper halves of Equation (3.14). The final step in achieving the Cooley-Tukey FFT is to recognize that the butterfly operation can be applied to adjoining data points if the data are rearranged in a specific manner: namely, input data elements i and j are exchanged where j, interpreted as a binary value, has the mirrored bit pattern of i. This two-step process of first rearranging the data and then performing the recursive butterfly operations is given in Algorithm 3.1. Most notably, the FFT is not an approximation of the DFT but, rather, provides identical data. The major disadvantage of the split-by-two approach is the restriction of the FFT to data lengths N to powers of 2. If N is not a power of 2, the sequence needs to be padded with zeros to the next power of 2, which may offset some of the computational advantage (e.g., a 640 x 480 pixel image needs to be padded to form a 1024 x 512 pixel image for FFT).
To understand the FFT, one needs to recognize that the summation in Equation (3.6) can be split in odd and even halves:
FIGURE 3.7 Reduction of an eight-point DFT into two four-point DFTs with eight subsequent multiplications and additions following Equation (3.14). Multiplication with the twiddle factors occurs along the diagonal lines. By using the same scheme, the four-point DFTs can be subdivided into two-point DFTs. The two-point DFT is the most fundamental operation and cannot be subdivided further.
The implementation of the FFT in Algorithm 3.1 is straightforward, although simple complex arithmetic needs to be provided with the FFT function. Some languages (e.g., FORTRAN) provide complex arithmetic. In C, a structure can be defined that contains two double-precision elements for the real and imaginary parts, respectively; simple complex arithmetic functions with two parameters that return the sum, difference, and product of the parameters need to be defined. In C++, the operators +, -, and * can be overloaded. A very efficient implementation of the FFT function that does not rely on external complex arithmetic is provided in Numerical Recipes in C.23 In the same topic, multidimensional FFT implementations are presented. Multidimensional FFTs can be made more efficient by using the symmetry of the exponential phase terms. Additional efficiency gains can be achieved when the input data are real-valued rather than complex-valued, which is almost always the case in image processing. Since many efficient implementations of the FFT exist, Algorithm 3.1 is provided for reference only. It is, of course, educational to implement the code in Algorithm 3.1 and monitor how the bit-reversal part and the Danielson-Lanczos algorithm operate.
One of the most advantageous options for performing an FFT is to use available FFT libraries. A freely available library can be accessed at http://www.fftw.org,11 where fftw is an acronym for the "Fastest Fourier Transform in the West." Those familiar with the fftw library have little reason to doubt the veracity of the developer’s claim. Not only does the fftw library contain several different algorithms optimized for different types of data in one or multiple dimensions, but a measurement function exists that determines the optimum algorithm for a given situation. Whereas the initial performance measurement constitutes computational overhead, the overall gain for the repeated use of the same FFT is considerable. For single FFT where the overhead is not justified, fftw estimates the optimum algorithm without additional computational effort. Another advantage of the fftw library is that input data are not restricted to power-of-2 sizes. Rather, fftw is capable of computing the FFT of arbitrary-sized data sets. Furthermore, fftw provides functions for real-valued input and contains code for the discrete sine and cosine transforms and the fast Hartley transform (see Section 3.3). With these capabilities, fftw is arguably the library of choice for most applications that call for discrete Fourier transforms and related integral transforms.
Algorithm 3.1 Fast Fourier transform in one dimension. This function depends on a complex input array data with N elements (0 to N – 1), where N must be a power of 2. The FFT function needs an external function swap that exchanges the two arguments. The variables v, w, and c are complex numbers. Furthermore, the symbols <g>, ®, and Q denote complex multiplication, addition, and subtraction, respectively. The Fourier transform takes place within the data array, and the output needs to be normalized, that is, all elements of data divided by N. The inverse Fourier transform is almost identical except that theta in part 2 has a negative sign, and no normalization takes place.