The support vector machine (SVM) (Boser et al., 1992; Vapnik, 1998; Cristianini and Shawe-Taylor, 2000) is a supervised learning algorithm, useful for recognizing subtle patterns in complex data sets. The algorithm performs discriminative classification, learning by example to predict the classifications of previously unseen data. The algorithm has been applied in domains as diverse as text categorization, image recognition, and hand-written digit recognition (Cristianini and Shawe-Tyalor, 2000). Recently, SVMs have been applied in numerous bioinformatics domains, including recognition of translation start sites, protein remote homology detection, protein fold recognition, microarray gene expression analysis, functional classification of promoter regions, prediction of protein-protein interactions, and peptide identification from mass spectrometry data (reviewed in Noble (2004)).
The popularity of the SVM algorithm stems from four primary factors. First, the algorithm boasts a strong theoretical foundation, based upon the dual ideas of VC dimension and structural risk minimization (Vapnik, 1998). Second, the SVM algorithm is well-behaved, in the sense that it is guaranteed to find a global minimum and that it scales well to large data sets (Platt, 1999a). Third, the SVM algorithm is flexible, as evidenced by the list of applications above. This flexibility is due in part to the robustness of the algorithm itself, and in part to the parameterization of the SVM via a broad class of functions, called kernel functions. The behavior of the SVM can be modified to incorporate prior knowledge of a classification task simply by modifying the underlying kernel function. The fourth and most important explanation for the popularity of the SVM algorithm is its accuracy. Although the underlying theory suggests explanations for the SVM’s excellent learning performance, its widespread application is due in large part to the empirical success the algorithm has achieved.
An early successful application of SVMs to biological data involved the classification of microarray gene expression data. Brown et al. (2000) used SVMs to classify yeast genes into functional categories on the basis of their expression profiles across a collection of 79 experimental conditions (Eisen et al., 1998). Figure 1 shows a subset of the data set, divided into genes whose protein products participate and do not participate in the cytoplasmic ribosome. The ribosomal genes show a clear pattern, which the SVM is able to learn relatively easily. The SVM solution is a hyperplane in the 79-dimensional expression space. Subsequently, a given gene’s protein product can be predicted to localize within or outside the ribo-some, depending upon the location of that gene’s expression profile with respect to the SVM hyperplane. SVMs have also been used successfully to classify along the other dimension of gene expression data: placing entire gene expression experiments into categories on the basis of, for example, the disease state of the individual from which the expression profile was derived (Furey et al., 2001; Ramaswamy et al., 2001; Segal et al., 2003).
Figure 1 Gene expression profiles of ribosomal and nonribosomal genes. The figure is a heat map representation of the expression profiles of 20 randomly selected genes. Values in the matrix are log ratios of the two channels on the array.An SVM can learn to differentiate between the characteristic gene expression pattern of ribosomal proteins and non-ribosomal proteins. The figure was produced using matrix2png (Pavlidis P and Noble WS (2003) Matrix2png: A utility for visualizing matrix data. Bioinfonnatics. 19(2). 295-296)
A scientist who wishes to apply support vector machine learning to a particular biological problem faces first the question of which kernel function to apply to the data. Essentially, the kernel function defines a notion of similarity between pairs of objects. In the case of gene expression data, for example, the kernel value for two genes with similar expression profiles will be large, and vice versa. Mathematically, the kernel function must follow certain rules in order for the SVM optimization to work properly. Specifically, the kernel must be positive semidefinite, meaning that, for any given data set, the square matrix of pairwise kernel values defined from that data set will have nonnegative eigenvalues. In practice, however, most users of SVM software do not have to worry about these mathematical details, because the software typically provides a relatively small collection of valid kernel functions to choose from.
In general, a good rule of thumb for kernel selection is to start simple. The simplest kernel function is a linear scalar product, in which the products of corresponding elements in each of the two items being compared are summed. Normalizing the kernel, which amounts to projecting the data onto a unit sphere, is almost always a good idea. Centering the kernel, so that the points lie around the origin, is also helpful, though this operation is difficult to perform properly if the (unlabeled) test data is not available during training.
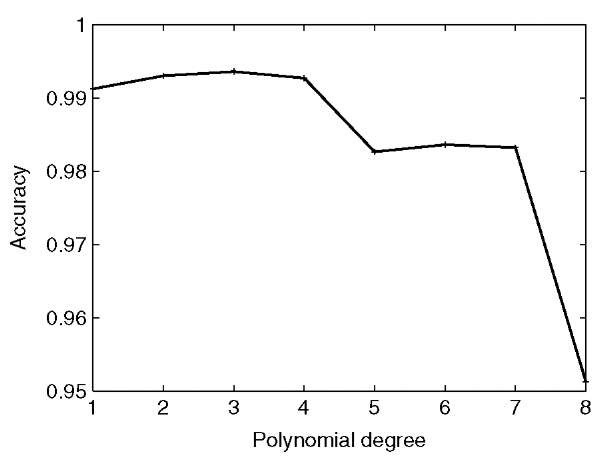
A slightly more complex class of kernel functions is the set of polynomials, in which the scalar product is raised to a positive power. The degree of the polynomial specifies the n-way correlations that the kernel takes into account. Thus, for the 79-element gene expression data mentioned above, a quadratic kernel implicitly accounts for all 79 x 79 = 6241 possible pairwise correlations among expression measurements. Obviously, as the polynomial degree gets larger, the number of features increases exponentially, eventually overwhelming the SVM’s learning ability. It is necessary, therefore, to hold out a portion of the labeled data from the training phase and to use that data to evaluate the quality of the trained SVM with different kernels. The use of a hold-out set is the basis of a more general technique known as cross-validation (Duda and Hart, 1973). Figure 2 shows the effect of the polynomial degree on the SVM’s ability to recognize members of the cytoplasmic ribosomal proteins. As the degree increases, accuracy improves slightly, but then drops again when the number of features becomes too large.
Besides polynomial kernels, the other common kernel is the radial basis function. This kernel warps the space where the data resides by putting a Gaussian over every data point. The kernel then measures similarities in that warped space. In this case, the user-controlled parameter is the width of this Gaussian. Like the polynomial degree parameter, the Gaussian width is typically selected via cross-validation. Some software will automatically select a reasonable (though not necessarily optimal) width by examining the average distance between positive and negative examples in the training set.
Figure 2 The effect of polynomial degree on SVM performance. The figure plots the classification accuracy of an SVM as a function of the polynomial degree. The SVM was trained to recognize ribosomal proteins, using data from Brown MPS, Grundy WN, Lin D, Cristianini N, Sugnet C, Furey TS, Ares Jr M and Haussler D (2000) Knowledge-based analysis of microarray gene expression data using support vector machines. Proceedings of the National Academy of Sciences of the United States of America, 97(1), 262-267 and using the Gist software with default parameters. Accuracy was measured using threefold cross-validation, repeated five times
The kernels discussed so far are applicable only to vector data, in which each object being classified can be represented as a fixed-length vector of real numbers. Gene expression data fits this paradigm, but many other types of biological data – protein sequences, promoter regions, protein-protein interaction data, and so on – do not. Often, it is possible to define a relatively simple kernel function from nonvector data by explicitly constructing a vector representation from the nonvector data and applying a linear kernel. For example, a protein can be represented as a vector of pairwise sequence comparison (BLAST or Smith-Waterman) scores with respect to a fixed set of proteins (Liao and Noble, 2002) or simply as a vector of 1′s and 0′s, indicating the presence or absence of all possible length-^ substrings within that protein (Leslie et al., 2002). Similarly, protein-protein interaction data for a given protein can be summarized simply as a vector of 1′s and 0′s, where each bit indicates whether the protein interacts with one other protein. Other, more complex kernels, such as the diffusion kernel (Kondor and Lafferty, 2002), can also be constructed without relying upon an explicit vector representation. In general, selecting the kernel function is analogous to selecting a prior when building a Bayesian model. Thus, while simple kernels often work reasonably well, much research focuses on the development of complex kernel functions that incorporate domain knowledge about particular types of biological data.
In addition to selecting the kernel function, the user must also set a parameter that controls the penalty for misclassifications made during the SVM training phase. For a noise-free data set, in which no overlap is expected between the two classes being discriminated, a hard margin SVM can be employed. In this case, the hyperplane that the SVM finds must perfectly separate the two classes, with no example falling on the wrong side. In practice, however, it is often the case that some small percentage of the training set samples are measured poorly or are improperly labeled. In such situations, the hard margin SVM will fail to find any separating hyperplane, and a soft margin must be employed instead. The soft margin incorporates a penalty term, and penalties are assigned to each misclassified point proportional to the point’s distance from the hyperplane. Thus, a misclassified point that is close to the hyperplane will receive a small penalty, and vice versa. SVM practitioners differ over whether a linear (1-norm) or quadratic (2-norm) penalty yields better performance in general; however, regardless of the type of penalty imposed, the proper magnitude of the penalty is definitely problem-specific. Hence, this penalty parameter is typically selected either using cross-validation or by minimizing the number of support vectors (i.e., nonzero weights) in the SVM training output. The effect of this soft margin parameter on SVM accuracy is typically large, outweighing the effect, for example, of polynomial degree shown in Figure 2.
Setting the soft margin parameter is further complicated when the relative sizes of the two groups of data being discriminated are skewed. In many pattern recognition problems, this type of skew is typical: the interesting (positive) class of examples is small, and it is being discriminated from a relatively large (negative) class of uninteresting examples. In such a situation, the soft margin must be modified to asymmetrically penalize errors in the two classes: making a mistake on one of the relatively few positive examples is much worse than making a mistake on one of the many negative examples. A reasonable heuristic is to scale the penalty according to the relative class sizes. Hence, if there are 10 times as many negative examples as positive examples, then each positive misclassification receives 10 times as much penalty. In general, the degree of asymmetry should depend upon the relative cost associated with false-positive and false-negative predictions.
So far, we have discussed the SVM only in the context of discriminating between two classes of examples (e.g., ribosomal and nonribosomal genes). Many prospective SVM users worry that the binary nature of the algorithm is a fundamental limitation. This is not the case. Generalizing the SVM to perform multiclass pattern recognition is trivial. The most straightforward, and often the most successful, means of carrying out this generalization is via a so-called one-versus-all training paradigm. In order to discriminate among n different classes of examples, n SVMs are trained independently. Each SVM learns to differentiate between one class and all of the other classes. A new object is classified by running it through each of the SVMs and finding the one that produces the largest output value. This approach has been used successfully, for example, to classify 14 types of cancer from gene expression profiles (Ramaswamy et al., 2001).
Finally, a desirable feature of any classification algorithm is the ability to produce probabilistic outputs. In general, an SVM produces a prediction that has no units. This discriminant score is proportional to the example’s distance from the hyperplane, so a large positive value implies high confidence that the example lies in the positive class. A relatively simple postprocessing step involving fitting a sigmoid curve can convert these discriminants to probabilities (Platt, 1999b).
Perhaps the easiest way for a novice to apply an SVM to a particular data set is via the web interface at svm.sdsc.edu. This server allows for the training of an SVM on a labeled data set. The SVM can then be used to make predictions on a second, unlabeled data set. Additional flexibility, including leave-one-out cross-validation and empirical curve fitting to get probabilistic outputs, is available by downloading the underlying Gist software (microarray.cpmc.columbia.edu/gist) (Pavlidis et al., 2004).