1. Introduction
The main objectives of experimental design are reducing variation, eliminating bias, and making the analysis of the data and the interpretation of the results as simple and as powerful as possible. This should occur with the purpose of the experiment in mind and within the practical constraints. Principles of statistical design of experiments were first introduced by Ronald A. Fisher in the 1920s for designing agricultural field trials. The relevance of his ideas has only increased since then. This article elucidates the main principles of designing efficient experiments and the statistical analysis thereof. It uses microarray experiments as an example.
2. Design principles: between variation and bias
The common aim of many scientific experiments is to establish the activity of a response of interest across several conditions or subpopulations. For example, how do DNA sequence repeats vary across different positions on the human genome? Sometimes, the conditions or populations of interest are defined through an active intervention of the part of the scientist. In this case, conditions are typically referred to as treatments. For example, plant scientists may be interested in the change in expression profiles for Arabidopsis plants as a result of fertilizer, seed dormancy, or vernalization treatments. Sometimes, a proxy for the response is necessary if the response itself is not directly measurable. Average spot intensity on a microarray is typically taken as the operative definition of gene expression. Different proxies might have different characteristics, and sometimes it is useful to consider several proxies simultaneously.
Despite having a measurable quantity, it is typically infeasible to measure that quantity for the whole population of interest, nor is it likely that this quantity for all members of the population will be the same. This necessitates taking a sample and, at least as important, one that is representative of the population as a whole.
Representative means that it should embody the population variation, without any bias toward any particular group within it.
The ideas behind a representative sample are crucial for experimental design and can be described by means of several design principles (see Article 52, Experimental design, Volume 7):
1. Replication: When access to experimental material is limited or requires substantial resources, there might be the temptation to make several measurements on the same or a nearby experimental unit. Unfortunately, such observations are almost certainly very similar and therefore fail to reflect the full variation present in the sample. True replication, sometimes called biological replication in the context of biological experiments, is a necessary condition for obtaining a representative sample.
2. Randomization: If experimenters are let to decide for themselves which experimental units receive which treatment, it is possible that intentionally or unintentionally one condition is favored over another. By making the assignment of the units to the conditions subject to, for example, a coin flip, any such bias of the effects and their variances can be avoided.
3. Blocking: Often, it is impossible to get homogeneous experimental materials, in which case a subdivision in more or less homogeneous blocks should be considered. Microarrays come in print batches, DNA pools come from PCR amplification runs, and so on. Even though blocking factors are not of primary interest, it is important not to ignore the variation they introduce. Typically, it is prudent to model blocking factors such as print batches explicitly.
4. Crossing: If one experimental condition is always observed jointly with another, then it is impossible to decide whether the observed effect in the response is due to one or the other. This is called confounding. In order to avoid this type of ambiguity, it is essential to cross conditions with each other, that is, making sure that the levels of experimental conditions do not always appear in tandem.
5. Balance: It makes intuitive sense that in order to get the best results, each condition should be measured more or less an equal amount of times. Although not essential for inference, this type of balance has many computational advantages and is generally recommended wherever possible.
Following these general principles, one converts unplanned systematic variability into planned, chance-like variability. It protects against possible bias, and makes subsequent statistical analysis possible.
3. Several standard designs
To implement the design principles, one should be led first and foremost by the requirements of the experimental situation. Sometimes, it is possible to make use of several standard designs that satisfy automatically all the necessary design conditions.
If the experimental sample is from a homogeneous population, then no blocking is needed and the conditions can be randomly assigned to the experimental units.
This is called a completely randomized design and is most useful in only the simplest of scientific experiments. A commonly used design is the randomized complete block design, developed in 1925 by R. A. Fisher. In this design, the experimental units are subdivided into more or less homogeneous “blocks” and within each block the treatments are randomly assigned to the units.
Sometimes, the blocks are too small in order to apply all the conditions of interest within each block. This is typically the case in microarray studies, where each array is a block and at most two conditions can be measured within each array. Incomplete block designs (IBD) are aimed to deal with this situation. A Latin Square design is an elegant example of an IBD. It crosses the condition of interest with two blocking factors in such a way that the design is balanced, but not each combination of factors is observed.
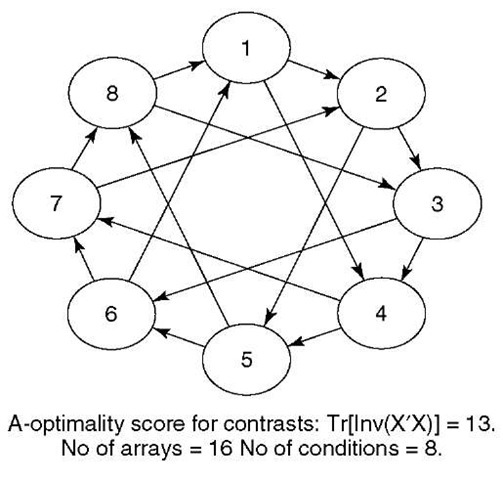
Two-channel microarray experiments can be regarded as experimental designs with block-size two. If more than two conditions are of interest, then the assignment of conditions to arrays can be particularly tricky. Many standard incomplete block designs do not apply in this case. A simple class of interwoven loop designs has been suggested (Kerr and Churchill, 2001b) and shown to have excellent efficiency properties (Wit et al., 2005). Figure 1 shows an example of an interwoven loop design for eight conditions, which consists of lining up the conditions in the an imaginary circle (in any order) and by hybridizing each condition with the condition that is 1 step and with the condition that is 3 steps down the circle respectively. An interwoven loop design should always contain a 1-step circle in order to guarantee that all the conditions are connected. The other jump sizes can either be chosen intuitively or with some optimization function, such as od in smida library in R (Wit and McClure, 2004). An additional advantage is that by its very definition interwoven loop designs are dye-balanced and avoid the need of using inefficient dye-swap designs.
Figure 1 An interwoven loop design is a special case of an incomplete block design with block-size two. This design has excellent efficiency properties and is balanced in the “nuisance” dye factor
4. Normalization and estimation of effects
If an experiment has been designed according to the above design principles, then Analysis of Variance (ANOVA) is a coherent technique to untangle the effects of interest from the nuisance effects (see Article 53, Statistical methods for gene expression analysis, Volume 7 and Article 59, A comparison of existing tools for ontological analysis of gene expression data, Volume 7). For example, in a microarray experiment, one would like to estimate the contribution of a particular condition to the gene expression of a particular gene, while correcting for the dye used for hybridization, the pin used for printing and the position of the spot on the array, and perhaps the batch number from which the microarray came. Classical ANOVA is by no means the only technique that is able to estimate the effects of interest. More recent (hierarchical) Bayesian modeling approaches are capable of doing very much the same thing. In this discussion, we focus on the classical ANOVA.
First of all, it is essential to determine the response of interest. Gene expression is typically measured as an optical intensity across several pixels (dual-channel arrays) or several probes (Affymetrix Gene Chip). Typically, these values are summarized in a single expression value, either by taking the mean, median, or by performing a somewhat more complicated operation (e.g., Li etal., 2003). Intensity is an essentially positive and often a multiplicative scale. We recommend applying a logarithmic transformation to the intensities before analysis (see also Kerr and Churchill, 2001a), although generalized log-transformations have also proved useful (Huber etal., 2003). For two-channel arrays, each array gives two expression values for each gene. Some studies interpret each channel as an independent observation (Kerr and Churchill, 2001a), whereas others prefer to take the log-ratio of each of these two values (Wit and McClure, 2004). The latter is safer, although more conservative.
Anything that contributes to variation in the response is known in the statistical literature as an effect. The idea behind ANOVA is to write the observed experimental quantity as a sum of contributing elements, which are the result of the varying experimental conditions. An ideal microarray experiment across nc conditions and ng genes would be modeled as
where one typically assumes that the noise term e is normally distributed with a fixed variance. The quantity \x stands for the overall expression level across the arrays Gt, measures the average deviation from that expression level \x for gene i, Cj, measures the average deviation from \x for condition j. Most importantly, (GC)ij stands for the differential expression of gene i with respect to level j. In particular, if for a particular gene i the quantities (GC)ij are zero across all j, then this gene is not differentially expressed under the experimental conditions. The term (GC)ij is an example of an interaction effect. This interaction effect allows the response to vary differently across the conditions for each of the genes.
Clearly, the model in equation (1) is too simplistic. Besides a random error term, practitioners know that in many experiments there are also systematic nuisance effects. These nuisance terms are related to experimental conditions only partially under the control of the experimenter, such as, for example, a dye effect, a spatial effect, a pin effect, an array effect, or a batch effect. Under the assumption that each of these factors influences the signal additively, a more complete model for describing the observed gene expression involves additional terms for each of them, which is given by
where s(i) and b (j) are functions that indicate the position of gene i on the array and the batch number of array j respectively. If the experiment uses printed dual-channel arrays, then also a dye term and a print pin term can be added. One can also add interaction terms of these nuisance effects. For example, a pin-batch interaction effect would model the fact that in a different microarray batch, the pin effects are probably different as the pins have most likely changed between different batch runs (Kerr and Churchill, 2001a).
The key element in an ANOVA is the F-test, evaluating the effect of each of the terms. These F-tests are typically summarized in an ANOVA table. See Table 1 for an example. Given that the number of terms in an ANOVA is limited, multiple testing is not particularly an issue and we recommend using the usual 0.05 cutoff for significance. Terms that have an associatedp-value (last column) less than the cutoff are deemed important. Biologically most important are the individual estimates of the differential expression terms, that is, the condition-gene interactions. The individual differential expression terms can be put to further scrutiny.
There are two types of effects: so-called fixed effects and random effects. Fixed effects are most common and assume that the condition or treatment underlying the effect is some individual entity. Examples are gene effects, dye, and spatial effects. Random effects are used to model the effects of elements that can be considered to come from a larger population. The microarray batch used in an experiment can be considered as a particular sample from all possible batches made by the particular producer. Random effects are used when the effect of the individual levels of the condition or treatment are not of any particular interest, but the overall influence of them collectively is something to be taken into consideration. When both fixed and random effects are used in modeling a particular, one speaks of a mixed effects model.
Table 1 ANOVA table for Arabidopsis example, using log gene expression ratios for 100 genes across the four distinct plant types and two different regions involving 16 microarrays
| Df | Sum sq | Mean sq | F-value | Pr(>F) | |
| Dye | 1 | 1314.42 | 1314.42 | 1302.02 | 0.000 |
| Pin | 3 | 1.09 | 0.36 | 0.36 | 0.782 |
| Condition | 7 | 72.81 | 10.40 | 10.30 | 0.000 |
| Gene | 96 | 101.01 | 1.05 | 1.04 | 0.378 |
| Array | 8 | 90.70 | 11.34 | 11.23 | 0.000 |
| Condition* gene | 693 | 3930.93 | 5.67 | 5.62 | 0.000 |
| Type*gene | 297 | 3474.29 | 11.70 | 11.58 | 0.000 |
| Region*gene | 99 | 134.99 | 1.36 | 1.35 | 0.018 |
| Type*region*gene | 297 | 321.65 | 1.08 | 1.07 | 0.235 |
| Residuals | 792 | 799.54 | 1.01 |
Wolfinger et al. (2001) introduced a mixed effect model in a microarray context. The difference between fixed and random effects is not always clear-cut – for example, should pins be considered fixed or random effects? Using random effects results in somewhat more conservative estimates (larger standard errors), although typically it does not affect the estimates of the fixed effects, for example, the differential expression parameters GC ij.
5. Design and analysis of a microarray experiment
We illustrate all the ideas in this article by means of a practical design and analysis of a stylized dual-channel microarray experiment. An experimenter wants to compare four genetically distinct types of Arabidopsis plants across two different regions of a country. It is of interest to compare the gene-expression values both across the genetic types as well as across region. We can therefore distinguish 4 x 2 = 8 separate conditions. Given the availability of 16 dual-channel microarrays, the way to obtain the best estimates of differential expression for each condition-pair is as shown in Figure 1 (Wit et al., 2005). Typical reference designs would merely measure each condition twice, whereas this interwoven loop design measures each condition four times. The microarrays contain 100 probes, associated with 100 different genes.
The resulting dataset contains 1200 log-expression ratios. The ANOVA table, shown in Table 1, can be obtained by most standard statistical software. We first consider the nuisance effects. By evaluating the p-values, it is clear that there is an important dye and array effect, although there is no evidence that the four pins used to print the arrays have any distorting effect on the gene expressions. After correcting for the array and dye effect, it is evident from the highly significant condition-gene interaction that there are at least some genes that are differentially expressed across the eight conditions. In particular, there is a lot of evidence for differentially expressed genes across the four Arabidopsis types. There is also evidence that the region from where the plants were harvested affects the gene expression, although no synergetic effect on gene expression of genetic type and region is observed.
6. Conclusions
In order to avoid obtaining useless data, it is essential to integrate the statistical analysis with the design of any complex scientific experiment. For example, sources of variation cannot be estimated if they are confounded in the experimental design. Using ANOVA, or Bayesian equivalents, has the advantage of combining the normalization process with the data analysis. Considerations of optimal design can be employed to obtain the most accurate estimates of the parameters of interest.