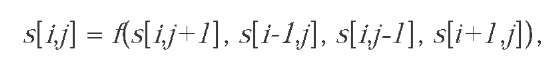INTRODUCTION
In recent years, the notion of complex systems proved to be a very useful concept to define, describe, and study various natural phenomena observed in a vast number of scientific disciplines. Examples of scientific disciplines that highly benefit from this concept range from physics, mathematics, and computer science through biology and medicine as well as economy, to social sciences and psychology. Various techniques were developed to describe natural phenomena observed in these complex systems. Among these are artificial life, evolutionary computation, swarm intelligence, neural networks, parallel computing, cellular automata, and many others. In this text, we focus our attention to one of them, i.e. ‘cellular automata’.
We present a truly discrete modelling universe, discrete in time, space, and state: Cellular Automata (CAs) (Sloot & Hoekstra, 2007, Kroc, 2007, Sloot, Chopard & Hoekstra, 2004). It is good to emphasize the importance of CAs in solving certain classes of problems, which are not tractable by other techniques. CAs, despite theirs simplicity, are able to describe and reproduce many complex phenomena that are closely related to processes such as self-organization and emergence, which are often observed within the above mentioned scientific disciplines.
BACKGROUND
We briefly explain the idea of complex systems and cellular automata and provide references to a number of essential publications in the field.
Complex Systems
The concept of complex systems (CSs) emerged simultaneously and often independently in various scientific disciplines (Fishwick, 2007, Bak, 1996, Resnick, 1997). This could be interpreted as an indication of their universality. Despite the diversity of those fields, there exist a number of common features within all complex systems. Typically a complex system consist of a vast number of simple and locally operating parts, which are mutually interacting and producing a global complex response. Self-organization (Bak, 1996) and emergence, often observed within complex systems, are driven by dissipation of energy and/or information.
Self-organization can be easily explained with ant-colony behavior studies where a vast number of identical processes, called ants, locally interact by physical contact or by using pheromone marked traces. There is no leader providing every ant with information or instructions what it should do. Despite the lack of such a leader or a hierarchy of leaders, ants are able to build complicated ant-colonies, feed their larvae, protect the colony, fight against other colonies, etc. All this is done automatically through a set of simple local interactions among the ants. It is well known that ants are responding on each stimuli by one out of 20 to 40 (depending on ant species) reactions, these are enough to produce the observed complexity.
Emergence is defined as the occurrence of new processes operating at a higher level of abstraction then is the level at which the local rules operate. Each level usually has its own local rules different from rules operating at other levels. An emergent, like an ant-colony, is a product of the process of emergence. There can be a whole hierarchy of emergents, e.g. as in the human body, that consists of chemicals and DNA, going through polypeptides, proteins, cellular infrastructures and cycles, further on to cells and tissues, organs, and bodies. We see that self-organization and emergence are often closely linked to one another.
Cellular Automata
Early development of CAs dates back to A. Turing, S. Ulam, and J. von Neumann. We can define CA’s by four mutually interdependent parts: the lattice and its variables, the neighbourhood, and the local rules (Toffoli & Margolus, 1987, Toffoli, 1984, Vichniac, 1984, Ilachinski, 2001, Wolfram, 2002, Wolfram 1994, Sloot & Hoekstra, 2007, Kroc, 2007). This is briefly explained below.
Lattices and Networks
A lattice is created by a grid of elements, for historical reasons called cells, which can be composed in one, two, three, or higher dimensional space. The lattice is typically composed of uniform cells such as, for instance squares, hexagons or triangles in two dimensions.
CAs operating on networks and graphs represent a generalization of classical CAs, which are working on regular lattices. Networks can be random or regular. Networks can have various topologies, which are classified by the degree of regularity and randomness. A lattice of cells can be interpreted as a regular network of vertices interconnected by edges. When we leave this regularity and allow some random neighbours, more precisely, if a major part of a network is regular and a smaller fraction of it is random, then we enter the domain of small-world networks. The idea of small-world networks provides a unique tool, which allows us to capture many essential properties of naturally observed phenomena especially those linked to social networks and surprisingly to (metabolic and other) networks operating within living cells. Whereas small-world networks are a mixture of regular and random networks, pure random networks have a completely different scope of use. It is worth to mention the concept of scale-free networks, which have a connectivity that does not depend on scale anymore (Kroc, 2007, Sloot, Chopard & Hoekstra, 2004).
Variables
A CA contains an arbitrary number of discrete variables. The number and range of them are dictated by the phenomenon under study. The simplest CAs are built using only one Boolean variable in one dimension (1D), see e.g. (Wolfram, 2002). Some of such simple 1D CAs express even high complexity and are shown to be capable of the universal computation.
Neighbourhoods
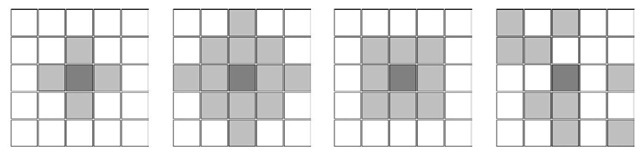
The neighbourhood, which is used to evaluate a local rule, is defined by a set of neighbouring cells including the updated cell itself in the case of regular lattices, Figure 1. Neighbours with relative coordinates [i,j+1], [i-1,j], [i, j-1], [i+1, j] of the updated cell [i, j] and located on North, West, South, and East, respectively, define the so called the von Neumann neighbourhood with radius r =1. The Moore neighbourhood with radius r =1 contains the same cells as the von Neumann neighbourhood plus diagonal cells located at relative positions [i-1, j+1], [i-1, j-1], [i+1, j-1], [i+1, j+1], i.e. North-west, South-west, South-east, and North-east, respectively.
There are many other types of neighbourhoods possible; neighbourhoods can even be spatially or temporally non-uniform. One example is the Margolus neighbourhood, used in diffusion modelling.
The boundaries for each CA can be fixed, reflecting or periodic. Periodic boundary conditions represent infinite lattices. Periodic means that, e.g. in one dimension, the most right cell of a lattice is connected to the most left lattice cell. Fixed boundary cells are kept at predefined values. Reflecting boundary cells reflect values back to the bulk of the lattice.
Local Rules
A local rule defines the evolution of each CA. Usually; it is realized by taking all variables from all cells within the neighbourhood and by evaluation of a set of logical and/or arithmetical operations written in the form of an algorithm. The vector s of those variables is updated according to the following local rule in the case of the von Neumann neighbourhood
Figure 1. Four types of neighbourhood is shown on the lattice of 5 x 5 cells: (from left) the von Neumann with r =1, and r =2, the Moore with r =1, and finally a random one
where i represents the x coordinate, j represents y coordinate of the cell, and f the local rule. The updated cell has coordinates [ij]. Figure 1 shows a 5×5 two-dimensional CA with neighbourhoods having various radiuses.
Modelling
Computational modeling is defined as a mathematical, numerical and/or computational description of a naturally observed phenomenon. It is essential in situations where the observed phenomena are not tractable by analytical means. Results are often validated against analytical solutions in special or simplified cases. Its importance has been shown in physics and chemistry and is continuously increasing in new fields such as biology, medicine, sociology, and psychology.
CELLULAR AUTOMATA MODELLING OF COMPLEX SYSTEMS
There is a constant influx of new ideas and approaches enriching the CA method. Within CA modelling of complex systems, there are distinct streams of research and their applications in various disciplines, these are briefly discussed in this section.
Classical cellular automata, with a regular lattice of cells, are used to model ferromagnetic and anti-ferromagnetic materials, solidification, static and dynamic recrystallization, laser dynamics, traffic flow, escape and pedestrian behaviour, voting processes, self-replication, self-organization, earthquakes, volcano activity, secure coding of information and cryptography, immune systems, living cells and tissue behaviour, morphological development, ecosystems, and many other natural phenomena (Sloot, Chopard & Hoekstra, 2004, Kroc, 2007, Illachinski, 2001). CAs were first used in the modelling of excitable media, such as heart tissue. CAs often outperforms other methods as, e.g., the Monte-Carlo method, especially for highly dissipa-tive systems. The main reason why CAs represents the best choice in modelling of many naturally observed complex phenomena is because CAs are defined above truly spatio-temporally discretized worlds. The inherent CA properties brings new qualities in models that are not principally achievable by other computational techniques.
An example of an advanced CA method is the Lattice Boltzmann method consisting of a triangular network of vertices interconnected by edges where generalized ‘liquid particles’ move and undergo collisions according a collision table. A model of a gas is created where conservation of mass, momentum and energy during collisions are enforced, which produce a fully discrete and simplified, yet physically correct micro dynamics. When operated in the right limits, they reproduce the incompressible Navier-Stokes equations and therefore are a model for fluid dynamics. Averaged quantities resulting from such simulations correspond to solutions of the Navier-Stokes equations (Sloot & Hoekstra, 2007, Rivet & Boon, 2001).
Classical CAs, using lattices, have many advantages over other approaches but some known disadvantages have to be mentioned. One of the disadvantages of CAs could be in the use of discrete variables. This restriction is by some authors removed by use of continuous variables, leading to generalized CAs. The biggest disadvantage of classical CAs is often found in the restricted topology of the lattice. Classical regular lattices fail to reproduce properties of many naturally observed phenomena. What led to the following development in CAs.
Generalized cellular automata, Darabos, Giacobini & Tomassini in (Kroc, 2007), are built on general networks, which are represented by regular, random, scale-free networks or small-world networks. A regular network can be created from a classical CA and its lattice where each cell represents a node and each neighbour is linked by an edge. A random graph is made from nodes that have randomly chosen nodes as neighbours. Within scale-free networks, some nodes are highly connected to other points whereas other nodes are less connected. Their properties are independent of their size. The distribution of degree of links at a node follow a power law relationship P(k) = k- g, where P(k) is the probability that a node is connect to k other nodes. The coefficient g is in most cases between 2 and 3. Those networks occur for instance in the Internet, in social networks, and in biologically produced networks such as gene regulatory networks within living cells or food chains within ecosystems (Sloot, Ivanov, Boukhanovsky, van de Vijver & Boucher, 2007).
In general, the behaviour of a given CA is unpredictable what is often used in cryptography. There exist a number of mostly statistical techniques enabling to study the behaviour of given CA but none of them is exact. The easiest way, and often the only one, to find out the state of a CA is its execution.
CASE STUDIES
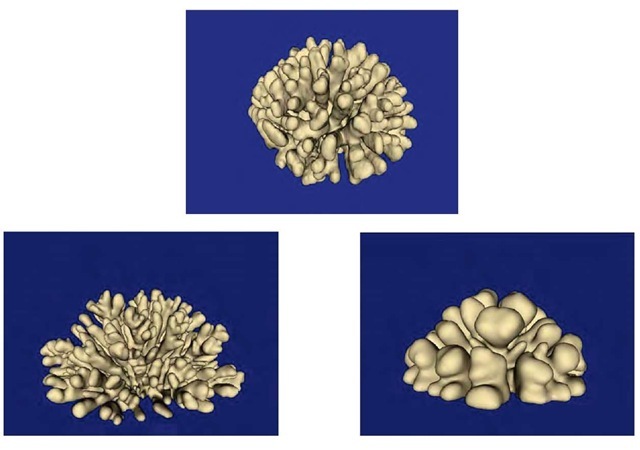
Understanding morphological growth and branching of stony corals with the lattice Boltzmann method is a good example of studying natural complex system with CAs (Kaandorp, Lowe, Frenkel & Sloot, 1996, Kaandorp, Sloot, Merks, Bak, Vermeij, & Maier, 2005). A deep insight into those processes is important to assess the role of corals in marine ecosystems and, e.g., its relation to global climate changes. Simulation of growth and branching of a coral involves multiphysics processes such as, nutrient diffusion, fluid flow, light absorption by the zooxanthele that live in symbiosis with the coral polyps, as well as mechanical stress.
It is demonstrated that nutrient gradients determine the morphogenesis of branching of phototropic corals. In this specific case, we deal with diffusion-limited processes fully determining the morphological shape of the growing corals. It is known from tank experiments and simulation studies that those diffusion dominant regions operate for relatively high flow velocitie s. It has been demonstrated that simulated coral morphologies are indistinguishable from real corals (Kaandorp, Sloot, Merks, Bak, Vermeij, & Maier, 2005), Figure 3.
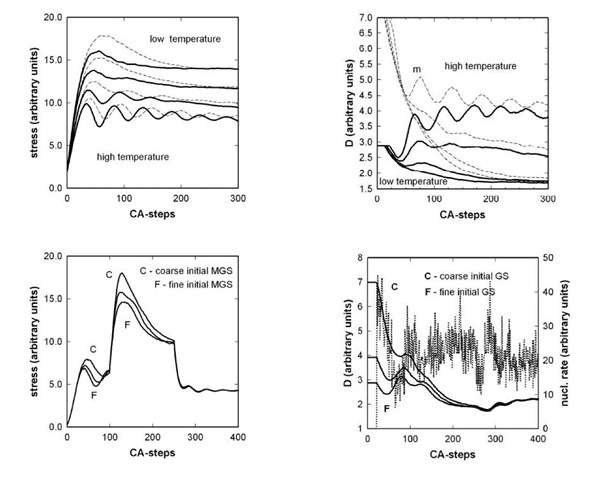
Modelling of dynamic recrystallization represents another living application of CAs within the field of solid state physics (Kroc, 2002). Metals having poly-crystalline form, composed from many single crystals, are deformed at elevated temperatures. The stored energy is increasing due to deformation, which is in turn released by recrystallization, where nuclei grow and form new grains. Growth is driven by the release of stored energy. The response of deformed polycrys-talline material is reflected by complex changes within the microstructure and deformation curve.
Stress-strain curves measured during deformation of metallic samples exhibits either single peak or multiple peak behaviour. This complex response of deformed material is a direct result of concurrent processes operating within deformed material. CAs, so far, represents the only computational technique, which is able to describe such complex material behaviour (Kroc, 2002), Figure 3.
FUTURE TRENDS
There is a number of distinct tracks within CAs research with a constant flux of new discoveries (Kroc, 2007, Sloot & Hoekstra, 2007). CAs are used to model physical phenomena but they are increasingly used to model biological, medical and social phenomena. Most CAs are designed by hand but the future requires development of automatic and self-adjusting optimization techniques to design local rules according to the needs of the described natural phenomena.
Figure 2. Morphological growth of coral Mandracis mirabilis obtained through 3D visualization of a CT-scan of the coral (top) and two simulated growth forms (bottom) with different morphological shapes are depicted (Kaandorp, Sloot, Merks, Bak, Vermeij, & Maier, 2005). Simulated structures are indistinguishable from real corals.
It is important to stress that the CA technique is bringing a cross-fertilization among many scientific disciplines. It happened many times in past that two or more very similar techniques were developed in distinct scientific fields such as, e.g. physics and social science.
The spatial structure of CAs is evolving from regular lattices to networked CAs Darabos, Giacobini, Tomassini in (Kroc, 2007), and to multilevel CAs (Hoek-stra, Lorentz, Fakone & Chopard, 2007). Updating schemes of CAs will address in the future two regimes: synchronous (the classical one), and asynchronous (Sloot, Overeinder & Schoneveld, 2001).
CONCLUSIONS
We briefly discussed complex systems and demonstrate the usefulness of cellular automata in modelling those systems. It has been shown that cellular automata provide a simple but an extremely efficient numerical technique, which is able to describe and simulate such complicated behaviour as self-organization and emergence. This extraordinary combination of simplicity and expressivity brings a constant flux of new discoveries in description of many naturally observed phenomena in almost all scientific fields.
Figure 3. Simulation of dynamic recrystallization is represented by: stress-strain curves (top-left), relevant mean grain size D-strain curves (top-right), an abrupt change loading strain rate (bottom-left), and relevant D-strain curves (bottom-right). Strain is represented by the number of CA steps (Kroc, 2002).
Finally, it is good to emphasize that CAs represent a generic method often used in the development of prototypes of completely new numerical methods describing naturally observed phenomena. We believe that CAs have a great potential for the future development of computational modelling and the understanding of the dynamics of complex systems.
KEY TERMS
Cellular Automaton: (plural: cellular automata.)A cellular automaton is defined as a lattice (network) of cells (automata) where each automaton contains a set of discrete variables, which are updated according to a local rule operating above neighbours of given cell in discrete time steps. Cellular automata are typically used as simplified but not simple models of complex systems.
Generalized Cellular Automaton: It is based on use of networks instead of regular lattices.
Complex Network: Most of biological and social networks reflect topological properties not observed within simple networks (regular, random). Two examples are small-world and scale-free networks.
Complex System: A typical complex system consists of a vast number of identical copies of several generic processes, which are operating and interacting only locally or with a limited number of not necessary close neighbours. There is no global leader or controller associated to such systems and the resulting behaviour is usually very complex.
Emergence: Emergence is defined as the occurrence of new processes operating at a higher level of abstraction then is the level at which the local rules operate. A typical example is an ant colony where this large complex structure emerges through local interactions of ants. For example, a whole hierarchy of emergents exists and operates in a human body. An emergent is the product of an emergence process.
Lattice Gas Automata: Typically, it is a triangular network of vertices interconnected by edges where generalized liquid particles move and undergo collisions. Averaged quantities resulting from such simulations correspond to solutions of the Navier-Stokes equations.
Modelling: It is a description of naturally observed phenomena using analytical, numerical, and/or computational methods. Computational modelling is classically used in such fields as, e.g. physics, engineering. Its importance is increasing in other fields such as biology, medicine, sociology, and psychology.
Random Network: A neighbourhood of a vertex is created by a set of randomly chosen links to neighbouring vertices (elements) within a network of vertices.
Regular Lattice: A perfectly regular and uniform neighbourhood for each lattice element called cell characterizes such lattices.
Self-Organization: Self-organization is a process typically occurring within complex systems where a system is continuously fed by energy, which is transformed into a new system state or operational mode by a dissipation of energy and/or information.
Self-Organized Criticality: A complex system expressing SOC is continuously fed by energy where release of it is discrete and typically occurs in the form of avalanches. Most of its time, SOC operates at a critical point where avalanches occur. Earthquakes and volcano eruptions represent prototypical examples of SOC observed in many naturally observed phenomena.
Small-World Network: A mixture of two different types of connections within each neighbourhood characterizes small-worlds. Typically, a neighbourhood of given vertex is composed of a greater fraction of neighbours having regular short-range connectivity (regular network) and a smaller fraction of random connections (random network). Such type of neighbourhood provides unique properties to each model built on the top of it.