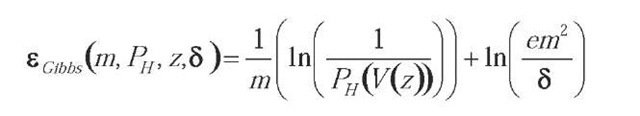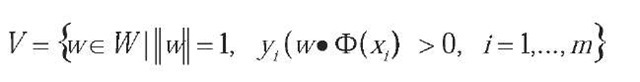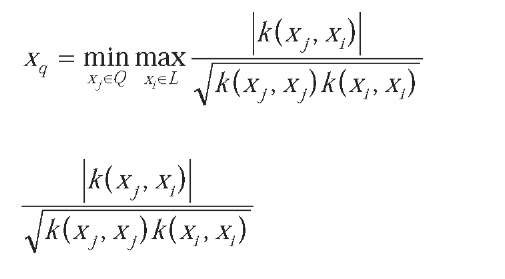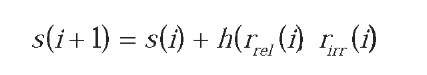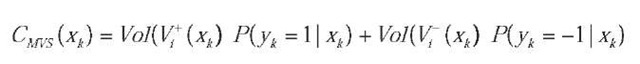INTRODUCTION
With the increasing demand of multimedia information retrieval, such as image and video retrieval from the Web, there is a need to find ways to train a classifier when the training dataset is combined with a small number of labelled data and a large number of unlabeled one. Traditional supervised or unsupervised learning methods are not suited to solving such problems particularly when the problem is associated with data in a high-dimension space. In recent years, many methods have been proposed that can be broadly divided into two groups: semi-supervised and active learning (AL). Support Vector Machine (SVM) has been recognized as an efficient tool to deal with high-dimensionality problems, a number of researchers have proposed algorithms of Active Learning with SVM (ALSVM) since the turn of the Century. Considering their rapid development, we review, in this chapter, the state-of-the-art of ALSVM for solving classification problems.
BACKGROUND
The general framework of AL can be described as in Figure 1. It can be seen clearly that its name – active learning – comes from the fact that the learner can improve the classifier by actively choosing the “optimal” data from the potential query set Q and adding it into the current labeled training set L after getting its label during the processes. The key point of AL is its sample selection criteria.
AL in the past was mainly used together with neural network algorithm and other learning algorithms. Statistical AL is one classical method, in which the sample minimizing either the variance (D. A. Cohn, Ghahramani, & Jordan, 1996), bias (D. A. Cohn, 1997) or generalisation error (Roy & McCallum, 2001) is queried to the oracle. Although these methods have strong theoretical foundation, there are two common problems limiting their application: one is how to estimate the posterior distribution of the samples, and the other is its prohibitively high computation cost. To deal with the above two problems, a series of version space based AL methods, which are based on the assumption that the target function can be perfectly expressed by one hypothesis in the version space and in which the sample that can reduce the volume of the version space is chosen, have been proposed. Examples are query by committee (Freund, Seung, Shamir, & Tishby, 1997), and SG AL (D. Cohn, Atlas, & Ladner, 1994). However the complexity of version space made them intractable until the version space basedALSVMs have emerged.
The success of SVM in the 90s has prompted researchers to combine AL with SVM to deal with the semi-supervised learning problems, such as distance-based (Tong & Koller, 2001), RETIN (Gosselin & Cord, 2004) and Multi-view (Cheng & Wang, 2007) based ALSVMs. In the following sections, we summarize existing well-known ALSVMs under the framework of version space theory, and then briefly describe some mixed strategies. Lastly, we will discuss the research trends for ALSVM and give conclusions for the chapter.
VERSION SPACE BASED ACTIVE LEARNING WITH SVM
The idea of almost all existing heuristic ALSVMs is explicitly or implicitly to find the sample which can reduce the volume of the version space. In this section, we first introduce their theoretical foundation and then review some typical ALSVMs.
Figure 1. Framework of active learning
| Initialize Step: An classifier h is trained on the initial labeled training set L | |
| step 1: | The learner evaluates each data x in potential query set Q (subset of or whole unlabeled data set U) and query the sample x*which has lowest EvalFun(x, L, h, H to the oracle and get its label y*; |
| step 2: | The learner update the classifier h with the enlarged training set {L + ( x*,
y*)}; |
| step 3: | Repeat step 1 and 2 until stopping training; |
| Where | |
| > | EvalFun(x, L, h, H): the function of evaluating potential query x (the lowest value is the best here) |
| > | L: the current labeled training set |
| > | H: the hypothesis space |
Version Space Theory
Based on the Probability Approximation Correct learning model, the goal of machine learning is to find a consistent classifier which has the lowest generalization error bound. The Gibbs generalization error bound (McAllester, 1998) is defined as
where PH denotes a prior distribution over hypothesis space H, V(z) denotes the version space of the training set z, m is the number of zand 5 is a constant in [0, 1]. It follows that the generalization error bound of the consistent classifiers is controlled by the volume of the version space if the distribution of the version space is uniform. This provides a theoretical justification for version space based ALSVMs.
Query by Committee with SVM
This algorithm was proposed by (Freund et al., 1997) in which 2k classifiers were randomly sampled and the sample on which these classifiers have maximal disagreement can approximately halve the version space and then will be queried to the oracle. However, the complexity of the structure of the version space leads to the difficulty of random sampling within it.
(Warmuth, Ratsch, Mathieson, Liao, & Lemmem, 2003) successfully applied the algorithm of playing billiard to randomly sample the classifiers in the SVM version space and the experiments showed that its performance was comparable to the performance of standard distance-based ALSVM (SD-ALSVM) which will be introduced later. The deficiency is that the processes are time-consuming.
Standard Distance Based Active Learning with SVM
For SVM, the version space can be defined as:
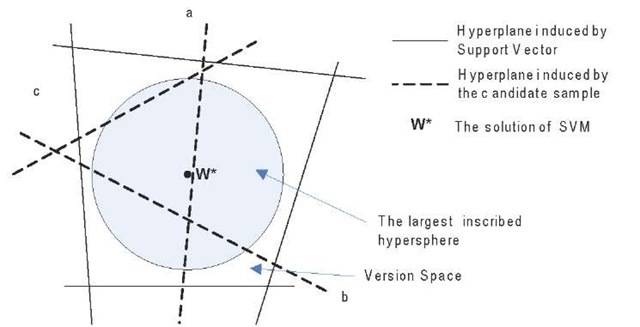
where ®(.) denotes the function which map the original input space Xinto a high-dimensional space ®(X), and W denotes the parameter space. SVM has two properties which lead to its tractability with AL. The first is its duality property that each point w in Vcorresponds to one hyperplane in ®(X) which divides 0( X) into two parts and vice versa. The other property is that the solution of SVM w* is the center of the version space when the version space is symmetric or near to its center when it is asymmetric.
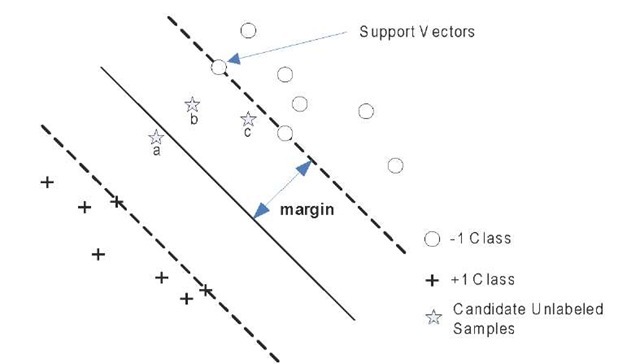
Based on the above two properties, (Tong & Koller, 2001) inferred a lemma that the sample nearest to the decision boundary can make the expected size of the version space decrease fastest. Thus the sample nearest to the decision boundary will be queried to the oracle (Figure 2). This is the so-called SD-ALSVM which has low additional computations for selecting the queried sample and fine performance in real applications.
Figure 2. Illustration of standard distance-based ALSVM
Figure 2a. The projection of the parameter space around the Version Space
Figure 2b. In the induced feature space
Batch Running Mode Distance Based Active Learning with SVM
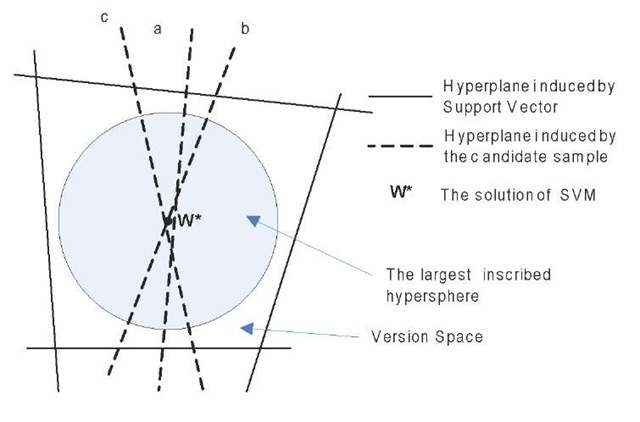
When utilizing batch query, (Tong & Koller, 2001) simply selected multiple samples which are nearest to the decision boundary. However, adding a batch of such samples cannot ensure the largest reduction of the size of version space, such as an example shown in figure 3. Although every sample can nearly halve the version space, three samples together can still reduce about 1/2, instead of 7/8, of the size of the version space. It can be observed that this was ascribed to the small angles between their induced hyperplanes.
To overcome this problem, (Brinker, 2003) proposed a new selection strategy by incorporating diversity measure that considers the angles between the induced hyperplanes. Let the labeled set be L and the pool query set be Q in the current round, then based on the diversity criterion the further added sample xq should be
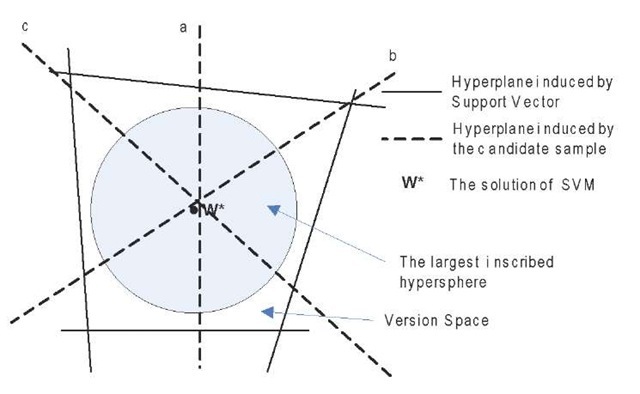
where denotes the cosine value of the angle between two hyperplanes induced by xj and xi, thus it is known as angle diversity criterion. It can be observed that the reduced volume of the version space in figure 4 is larger than that in Figure 3.
Figure 3. One example of simple batch querying with “a”, “b” and “c” samples with pure SD-ALSVM
Figure 4. One example of batch querying with “a”, “b” and “c” samples by incorporating diversity into SD-ALSVM
RETIN Active Learning
Let (Ij) je[1...n ] be the samples in a potential query set Q, and r(i, k) be the function that, at iteration i, codes the position k in the relevance ranking according to the distance to the current decision boundary, then a sequence can be obtained as follows:
In SD-ALSVM, s(i) is such as /,. ,,,…,/,. ,, ,
‘ v ‘ r(i,s(i) ‘ ‘ r(i,s(i)+m-1
are the m closest samples to the SVM boundary. This strategy implicitly relies on a strong assumption: an accurate estimation of SVM boundary. However, the decision boundary is usually unstable at the initial iterations. (Gosselin & Cord, 2004) noticed that, even if the decision boundary may change a lot during the earlier iterations, the ranking function r() is quite stable. Thus they proposed a balanced selection criterion that is independent on the frontier and in which an adaptive method was designed to tune s during the feedback iterations. It was expressed by
where h(x, y) = k x (x – y) which characterizes the system dynamics (k is a positive constant), rrel(i) and rirrl(i) denote the number of relevant and irrelevant samples in the queried set in the ith iteration. This way, the number of relevant and irrelavant samples in the queried set will be roughly equal.
Mean Version Space Criterion
(He, Li, Zhang, Tong, & Zhang, 2004) proposed a selection criterion by minimizing the mean version space which is defined as
where Vol (V+ (xk) (Vol (V~ (xk)) denotes the volume of the version space after adding an unlabelled sample xk into the ith round training set. The mean version space includes both the volume of the version space and the posterior probabilities. Thus they considered that the criterion is better than the SD-ALSVM. However, the computation of this method is time-consuming.
Multi-View Based Active Learning
Different from the algorithms which are based only on one whole feature set, multi-view methods are based on multiple sub-feature ones. Several classifiers are first trained on different sub-feature sets. Then the samples on which the classifiers have the largest disagreements comprise the contention set from which queried samples are selected. first (I. Muslea, Minton, & Knoblock, 2000) applied in AL and (Cheng & Wang, 2007) implemented it with ALSVM to produce a Co-SVM algorithm which was reported to have better performance than the SD-ALSVM.
Multiple classifiers can find the rare samples because they observe the samples with different views. Such property is very useful to find the diverse parts belonging to the same category. However, multi-view based methods demand that the relevant classifier can classify the samples well and that all feature sets are uncorrelated. It is difficult to ensure this condition in real applications.
MIXED ACTIVE LEARNING
Instead of single AL strategies in the former sections, we will discuss two mixed AL modes in this section: one is combining different selection criteria and another is incorporating semi-supervised learning into AL.
Hybrid Active Learning
Contrast to developing a new AL algorithm that works well for all situations, some researchers argued that combining different methods, which are usually complementary, is a better way, for each method has its advantages and disadvantages. The intuitive structure of the hybrid strategy is parallel mode. The key point here is how to set the weights of different AL methods.
The simplest way is to set fixed weights according to experience and it was used by most existing methods. The Most Relevant/Irrelevant (L. Zhang, Lin, & Zhang, 2001) strategies can help to stabilize the decision boundary, but have low learning rates; while standard distance-based methods have high learning rates, but have unstable frontiers at the initial feedbacks. Considering this, (Xu, Xu, Yu, & Tresp, 2003) combined these two strategies to achieve better performance than only using a single strategy. As stated before, the diversity and distance-based strategies are also complementary and (Brinker, 2003), (Ferecatu, Crucianu, & Boujemaa, 2004) and (Dagli, Rajaram, & Huang, 2006) combined angle, inner product and entropy diversity strategy with standard distance-based one respectively.
However, the strategy ofthe fixed weights can not fit well into all datasets and all learning iterations. So the weights should be set dynamically. In (Baram, El-Yaniv, & Luz, 2004), all the weights were initialized with the same value, and were modified in the later iterations by using EXP4 algorithm. In this way, the resulting AL algorithm is empirically shown to consistently perform almost as well as and sometimes outperform the best algorithm in the ensemble.
Semi-Supervised Active Learning
1. Active Learning with Transductive SVM
In the first stages of SD-ALSVM, a few labeled data may lead to great deviation of the current solution from the true solution; while if unlabeled samples are considered, the solution may be closer to the true solution. (Wang, Chan, & Zhang, 2003) showed that the closer the current solution is to the true one, the larger the size of the version space will be reduced. They incorporated Transductive SVM (TSVM) to produce more accurate intermediate solutions. However, several studies (T. Zhang & Oles, 2000) challenged that TSVM might not be so helpful from unlabeled data in theory and in practice. (Hoi & Lyu, 2005) applied the semi-supervised learning techniques based on the Gaussian fields and Harmonic functions instead and the improvements were reported to be significant.
2. Incorporating EM into Active Learning
(McCallum & Nigam, 1998) combined Expectation Maximization (EM) with the strategy of querying by committee. And (Ion Muslea, Minton, & Knoblock, 2002) integrated Multi-view AL algorithm with EM to get the Co-EMT algorithm which can work well in the situation where the views are incompatible and correlated.
FUTURE TRENDS
How to Start the Active Learning
AL can be regarded as the problem of searching target function in the version space, so a good initial classifier is important. When the objective category is diverse, the initial classifier becomes more important, for bad one may result in converging to a local optimal solution, i.e., some parts of the objective category may not be correctly covered by the final classifier. Two-stage (Cord, Gosselin, & Philipp-Foliguet, 2007), long-term learning (Yin, Bhanu, Chang, & Dong, 2005), and pre-cluster (Engelbrecht & BRITS, 2002) strategies are promising.
Feature-Based Active Learning
In AL, the feedback from the oracle can also help to identify the important features, and (Raghavan, Madani, & Jones, 2006) showed that such works can improve the performance of the final classifier significantly. In (Su, Li, & Zhang, 2001), Principal ComponentsAnalysis was used to identify important features. To our knowledge, there are few reports addressing the issue.
The Scaling of Active Learning
The scaling of AL to very large database has not been extensively studied yet. However, it is an important issue for many real applications. Some approaches have been proposed on how to index database (Lai, Goh, & Chang, 2004) and how to overcome the concept complexities accompanied with the scalability of the dataset (Panda, Goh, & Chang, 2006).
CONCLUSION
In this chapter, we summarize the techniques of ALSVM which have been an area of active research since 2000. We first focus on the descriptions of heuristic ALSVM approaches within the framework of the theory of version space minimization. Then mixed methods which can complement the deficiencies of single ones are introduced and finally future research trends focus on techniques for selecting the initial labeled training set, feature-based AL and the scaling of AL to very large database.
KEY TERMS
Heuristic Active Learning: The set of active learning algorithms in which the sample selection criteria is based on some heuristic objective function. For example, version space based active learning is to select the sample which can reduce the size of the version space.
Hypothesis Space: The set of all hypotheses in which the objective hypothesis is assumed to be found.
Semi-Supervised Learning: The set of learning algorithms in which both labelled and unlabelled data in the training dataset are directly used to train the classifier.
Statistical Active Learning: The set of active learning algorithms in which the sample selection criteria is based on some statistical objective function, such as minimization of generalisation error, bias and variance. Statistical active learning is usually statistically optimal.
Supervised Learning: The set of learning algorithms in which the samples in the training dataset are all labelled.
Unsupervised Learning: The set of learning algorithms in which the samples in training dataset are all unlabelled.
Version Space: The subset of the hypothesis space which is consistent with the training set.