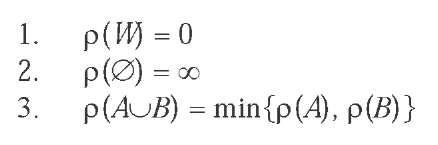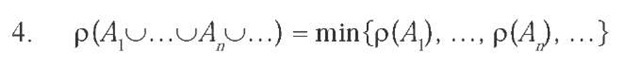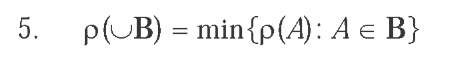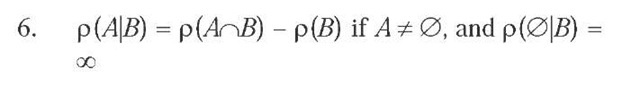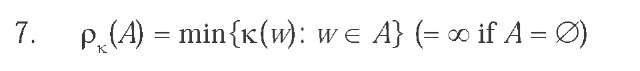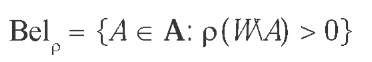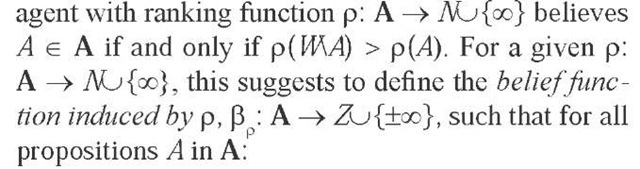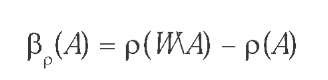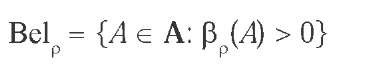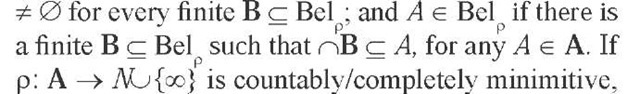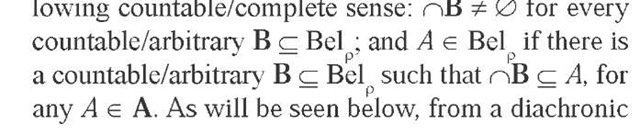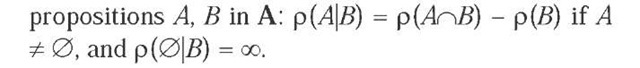INTRODUCTION
Ranking functions have been introduced under the name of ordinal conditional functions in Spohn (1988; 1990). They are representations of epistemic states and their dynamics. The most comprehensive and up to date presentation is Spohn (manuscript).
BACKGROUND
The literature on knowledge, belief, and uncertainty in artificial intelligence is divided into two broad classes. In epistemic logic (Hintikka 1961, Halpern & Fagin & Moses & Vardi 1995), belief revision theory (Alchour-ron & Gardenfors & Makinson 1985, Gardenfors 1988, Rott 2001), and nonmonotonic reasoning (Kraus & Lehmann & Magidor 1990, Makinson 2005) qualitative approaches are used to represent the epistemic state of an agent. In probability theory (Pearl 1988, Jeffrey 2004) and alternatives (Dempster 1968, Shafer 1976, Dubois & Prade 1988) epistemic states are represented quantitatively as degrees of belief rather than yes-or-no beliefs (see Halpern 2003 for an overview). One ofthe distinctive features of ranking functions is that they are quantitative, but nevertheless induce a notion of yes-or-no belief that satisfies the standard requirements of rationality, viz. consistency and deductive closure.
RANKING FUNCTIONS
Let Wbe a non-empty set of possibilities or worlds, and let A be a field of propositions over W That is, A is a set of subsets of Wthat includes the empty set 0(0 e A) and is closed under complementation with respect to W (if A e A, then WA e A) and finite intersection (if A e A and B e A, then AnB e A). A function p from the field A over Winto the natural numbers Nextended by <x>, p: A ^ NO {<x>}, is a (finitely minimitive) ranking function on A if and only if for all propositions A, B in A:
If the field of propositions A is closed under countable intersection (if A, e A, …, A e A, …, n e N, then
function p on A is countably minimitive ii and only ii it holds for all propositions A1 e A,. An e A, .
If the field of propositions A is closed under arbitrary intersection (if B c A, then nB e A) so that A is a y-field, a ranking function p on A is completely minimitive if and only if it holds for all sets of propositions B c A:
A ranking function p on A is regular just in case p(A) < <x> for each non-empty or consistent proposition A in A.
The conditional ranking function p(-|-): Ax A ^ No {<x>} based on the ranking function p on A is defined such that for all propositions A, B in A:
p(-|B) is a ranking function on A, for each proposition B in A.
A function k from the set of worlds Win to the natural numbers N, k: W^ N, is a pointwise ranking function on Wif and only if k(W = 0 for at least one world w in W. Each pointwise ranking function k on Winduces a regular and completely minimitive ranking function pK on every field of propositions A over Wby defining
Huber (2006) discusses under which conditions a ranking function on a field of propositions A induces a pointwise ranking function on the underlying set of worlds W
The rank of a proposition A, p(A), represents the degree to which an agent with ranking function p disbelieves A. If p(A) = 0, the agent does not disbelieve A. However, this does not mean that she believes A. She may well suspend judgment and neither disbelieve A nor its complement or negation WA (in this case p(A) = p( WA) = 0). Rather, belief in a proposition is characterized by disbelief in its negation: an agent with ranking function p: A ^ NO{<x>} believes A e A if and only if p( W\a) > 0. The belief set Belp of an agent with ranking function p: A ^ NO{<x>} is the set of all propositions she believes:
The axioms of ranking theory require an agent to not disbelieve both a proposition and its negation – i.e. at least one of A, W\A has to be assigned rank 0. Thus an
Pp assigns positive numbers to the propositions that are believed, negative numbers to the propositions that are disbelieved, and 0 to those propositions and their negations with respect to which the agent suspends judgment. As a consequence,
Belp is consistent and deductively closed in the finite sense, for every ranking function p on A. That is, nB
Bel is consistent and deductively closed in the fol-
point of view the converse is true as well. However, first we have to discuss how an epistemic agent is to update her ranking function when she learns new information.
UPDATE RULES
A theory of epistemic states is incomplete if it does not account for the way the epistemic states are updated when the agent receives new information. As there are different formats in which the agent may receive new information, there are different update rules. The simplest and most unrealistic case is that of the agent becoming certain of a new proposition. This case is covered by
Plain Conditionalization
If the agent’s epistemic state at time t is represented by the ranking function p on A, and if, between t and t’, the agent becomes certain of the proposition E e A and of no logically stronger proposition E+ c E, E+ e A, then the agent’s epistemic state at time t’ should be represented by the ranking function p’ = p(-\E) on A.
We usually do not learn by becoming certain of a proposition, though. In most cases the new information merely changes the strength of our beliefs in various propositions. This is illustrated by a variation of an example due to Jeffrey (1983). Let our agent be interested in the color of the carpet of her hotel room. At time t, before checking in, she neither believes nor disbelieves any of the following three hypotheses: the carpet is beige (beige), the carpet is brown (brown), the carpet is black (black). However, she is certain that the carpet is either beige or brown or black. The relevant part of her ranking function at time t thus looks as follows: p (beige) = p(not beige) = p (brown) = p(not brown) = p (black) = p(not black) = p (beige or brown or black) = 0, p(neither beige nor brown nor black) = <x>.
At time f, after checking in and when opening the door to her room, it appears to the agent that the carpet is rather dark. As a consequence she now believes that the carpet is either brown or black. But since it is late at night, the curtains are closed, and she has not turned on the light yet, she cannot tell whether the carpet is brown or black. Her ranks for the relevant propositions thus change to the following values: p’(beige) = p’ (not brown) = p’(not black) = 1, p’(not beige) = p’ (brown) = p’ (black) = 0.
A change in the strength of the agent’s beliefs about the color of the carpet will affect the strength of her beliefs about the color of, say, the furniture in the hotel room. For instance, at time t, our agent is pretty confident that the hotel room does not have dark furniture if the carpet is brown – and similarly if the carpet is black. She is also pretty confident that the hotel room has dark furniture if the carpet is beige. The relevant part of her ranking function at time t looks as follows: p(dark\brown) = p(dark|black) = 3, p(dark\beige) = 0. This implies that, at time t, the agent neither believes the furniture is dark nor that it is not dark, p(dark) = p(not dark) = 0.
The important question now is how the agent should update the rest of her ranking function (including the ranks for the propositions about the color of the furniture) when her ranks for the propositions about the color of the carpet change as specified above. The answer, already formulated in Spohn (1988), is given by
Spohn Conditionalization
If the agent’s epistemic state at time t is represented by the ranking function p on A, and if, between t and t’, the agent’s ranks on the partition {E_i \in \begin{cal}A\ end{cal}: E_i \in I} change to n_i \in N\cup{\infty} with min_i{n_i}=0 (n_i=0 if E_i=Wandn_i=\infty if E_i=\emptyset), and the agent’sfinite ranks change on no finer partition, then the agent’s epistemic state at time t’ should be represented by the ranking function p’ = min{p(-\E1) + rr …, p(-\Ej + rn, …} on A.
Applied to our example this means that, at time t, the agent’s rank for the proposition that the furniture is dark should be p’ (dark) = min{p (dark\beige) + 1, p (dark\brown) + 0, p(dark\black) + 0} = 1. That is, at time f, the agent believes, if only very weakly, that the furniture is not dark.
Spohn Conditionalization covers Plain Condition-alization as a special case. Shenoy (1991) presents an update rule for evidence of a still different format.
JUSTIFICATION
Ranking theory tells an epistemic agent how to organize her beliefs, and how to update her beliefs when she receives new information of various formats. Why should the agent follow those prescriptions?
The answer to this question requires a bit ofterminol-ogy. An agent’s degree of entrenchment for the proposition A is the number of information sources providing the information A that it takes for the agent to give up her disbelief in A. If the agent does not disbelieve A to begin with, her degree of entrenchment for A is 0. If no finite number of information sources providing the information A makes the agent give up her disbelief in A, her degree of entrenchment for A is <x>.
Degrees of entrenchment are used to measure an epistemic agent’s degrees of disbelief. If you want to measure my degree of disbelief for the proposition that Madrid is the capitol of Spain, you put me on a busy plaza in the center of Madrid and count the number of people passing by and telling me that Madrid is the capitol of Spain. My degree of entrenchment for the proposition that Madrid is the capitol of Spain equals n just in case I stop disbelieving that Madrid is the capitol of Spain after n people have passed by and told me it is – provided all those people are independent and equally reliable, indeed minimally positively reliable. Most people (and certainly all people in Madrid) are more than minimally positively reliable, though. An agent’s degree of disbelief in A is therefore defined as the number of information sources providing the information A that it would take for the agent to give up her disbelief that A if those information sources were independent and minimally positively reliable.
Now we can explain why an agent’s degrees of disbelief should obey the ranking calculus and thus be ranks, and why she should update her ranks according to Spohn Conditionalization. She should do so because doing so is necessary and sufficient for her to always have consistent and deductively closed beliefs. More precisely, Huber (2007) proves the following.
Consistency Theorem
An agent’s belief set is and will always be consistent and deductively closed in thefinite/countable/complete sense (and possibly conditional on some evidential proposition) if and only if this agent’s degree of disbelief function is a finitely/countable/completely minimitive ranking function and the agent updates according to Plain/Spohn/Shenoy Conditionalization when she receives information ofthe appropriate format.
Seen this way, the axioms and update rules of ranking theory are nothing but a diachronic version of consistency and deductive closure.
FUTURE TRENDS
One question in artificial intelligence is how an agent should update her epistemic state if she learns new conceptual information without also learning anything factual about the world she lives in. There are several ways in which such a conceptual change may occur. The agent may learn a new concept as when an enological ignoramus learns the concept barrique. Or the agent may learn that she has omitted a possibility from her set of worlds as when an enological ignoramus learns that there are rose wines besides red and white wines. All these conceptual changes involve the adoption of a new set of worlds W and, consequently, a new field of propositions A on the side of the agent. None of these conceptual changes seems to be adequately modeled by any of the formalisms mentioned at the beginning. Ranking theory is able to adequately model those conceptual changes by employing the so called ur or tabula rasa ranking – i.e. that ranking function that assigns rank 0 to every proposition. If the agent adds new possibilities to her set of worlds she should simply assign rank 0 to all those new possibilities. Similarly in case the agent replaces the old worlds by richer worlds. Huber (2009) discusses this and other future trends.
CONCLUSION
Ranking functions are an indispensable tool for artificial intelligence. First, they seem to adequately model most if not all of those phenomena that are dealt with in both qualitative as well as quantitative approaches to uncertainty. Second, they provide a link between these two classes of approaches that has been missing so far. Third, they can deal with phenomena that neither qualitative nor quantitative approaches seem to be able to deal with.
KEY TERMS
Belief: An agent with ranking function p: A ^ NO{<x>} believes A if and only if p( WA) > 0 – equiva-lently, if and only if p( WA) > p(A).
Belief Set: The belief set of an agent with ranking function p: A ^ NO{<x>} is the set of propositions the agent believes, Belp = {A e A: p( WA) > 0}.
Conditional Ranking Function: The conditional ranking function p(-|-): AxA ^ AU{<x>} based on the ranking function p on A is defined such that for all
Completely Minimitive Ranking Function: A ranking function p on a y-field of propositions A is completely minimitive if and only if p (uB) = min{p (A): A e B} for each set of propositions B c A.
Countably Minimitive Ranking Function: A ranking function p on a c-field of propositions A is countably minimitive if and only if p(A1u^uAnu) = min{p(A1), …, p(An), …} for all propositions A1 e A,… A e A, …
Pointwise Ranking Function: A function k from the set of worlds Win to the natural numbers N, k: W N, is a pointwise ranking function on W if and only if k(w) = 0 for at least one world w in W.
Degree of Disbelief: An agent’s degree of disbelief in the proposition A is the number of information sources providing the information A that it would take for the agent to give up her disbelief that A if those information sources were independent and minimally positively reliable.
Degree of Entrenchment: An agent’s degree of entrenchment for the proposition A is the number of information sources providing the information A that it takes for the agent to give up her disbelief in A.
Ranking Function: A function p on a field of propositions A over a set of worlds W into the natural numbers extended by <x>, p: A ^ AU{<x>}, is a (finitely minimitiv£) ranking function on A if and only if for all propositions A, B in A: p( W = 0, p(0) = <», p(AuB) = min{p(A), p(B)}.