In Depth Tutorials and Information

Kinematics (Advanced Methods in Computer Graphics) Part 2

Linear and Angular Velocity

In addition to the position and the orientation, the velocity of the end effector is also an important parameter in many applications involving a serial chain. For example, an articulated character model may be required to move an object with constant velocity. The velocity of the end effector is a combination of the linear velocity of the chain itself and the angular velocity introduced by the joint rotations.

Fig. 6.6 Velocity vectors on a single link in two-dimensional space

Velocity in Two Dimensions

First, we consider a single link AB that can move on the xy-plane, and rotate about the point A (Fig. 6.6). The position of the link at any instant is defined by the coordinates (xa, ya) of the point A. The point B takes the role of the end effector. The orientation of the link is measured by the angle 9 made by the link with the direction of the x-axis. The linear velocity of the link is the instantaneous speed with which it is moved from its current position A. If (Ax, Ay) denote the change in the position of the link from A in an infinitesimal interval of time At, the linear velocity components are given by

The angular velocity ! of the link is defined as the instantaneous change in the rotation angle 9 :

The direction of angular velocity is perpendicular to the xy-plane. If k is a unit vector along the z-direction, the angular velocity vector is

The linear velocity v9 of the point B induced by the above rotation is tangential to the circular arc with radius r at B (Fig. 6.6). This velocity is relative to the point A. If r denotes the vector from A to B given by (xb — xa, yb — ya), then v9 is defined as the following vector cross product:

The total velocity of the end effector B relative to the coordinate frame is simply the vector sum

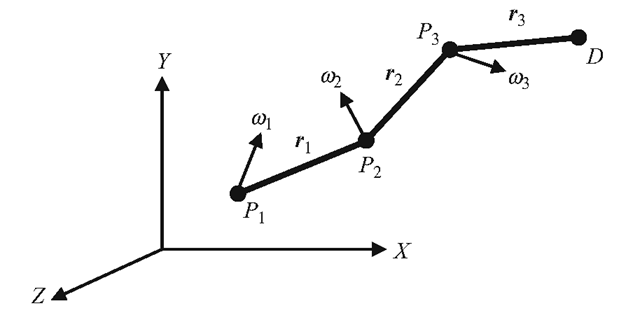
Now consider a three-link joint chain on the xy-plane, shown in Fig. 6.3. We define the vectors r1, r2, r3 along the links as follows:

The linear velocity v6 of the end effector E induced by the three joint angle rotations is given by

where is a unit vectoralong the z-axis.

Therefore

The total velocity of the end effector E is v6 + va where va is the velocity of the chain induced by the translational movement of the base A. As a particular case of Eq. 6.13, if p is a vector from A to B that undergoes only a rotational motion about A, then the linear velocity of the point B is given by

Velocity Under Euler Angle Transformations

The animation of a general serial chain in a three-dimensional space can be performed using Euler angle rotations (see Eq. 5.30) applied at the joints. In an extrinsic composition of rotations, the axes of rotation are fixed relative to the joint chain. In such a case, if the Euler angle sequence is given by f f, ¢, 6g as described in Sect. 5.4.1, the angular rate vector has the following form:

Fig. 6.7 Angular velocity vectors on a joint chain in three-dimensional space

Let us now consider a joint chain that is transformed using Euler angle rotations, as shown in Fig. 6.7.

Each joint P, (i = 1, 2, 3) has a set of Euler angles f f ; ¢, 9,-} from which we can construct a rotational transformation matrix R, using Eq. 5.30, and an angular velocity vector «,■ using Eq. 6.19. If di is the length of ,th link, the vectors r, along the link directions can be computed as

The linear velocity v9 of the end effector E resulting from the changes in the Euler angles can now be computed using Eq. 6.16. We add this velocity to the translational velocity of the joint chain at the base Pi to get the total velocity of the end effector E with respect to the reference frame.

Quaternion Velocity

We know that if P = (0, p) is a pure quaternion, and Q a unit quaternion, then the equation P’ = QPQ* gives a rotational transformation of the vector p, where P’ = (0,p’). The quaternion transformation can be viewed as defining the orientation of an object where p is a vector specified in a body-fixed frame, and p0 the same vector in the fixed (inertial) coordinate reference frame. Differentiating both sides and noting that p is a constant vector,

The inverse transformation for P is given by P = Q*P’Q. Substituting this expression in the above equation, we get

Since Q is a unit vector, QQ* = 1. Therefore,

Differentiating both sides of the equation QQ* = 1, we also find that

The above equation shows thatIn other words, the real part of the quaternion Q Q* is zero. Hence Q Q *can be expressed in the form (0, v). With these observations, Eq. 6.23 becomes

Using the quaternion multiplication rule in Eq. 5.11, we get

Since we consider only rotational motion of the vector p’, its linear velocity is given by Eq. 6.18. Comparing both equations, we find that ! = 2v. Hence we can write

where ! is the angular rate. Conversely, if a vector is rotated using a unit quaternion Q, the angular rate is given by the vector part of the quaternion product 2 Q Q *. Using Eq. 5.13, we can write this relationship in matrix form as given below.