3.2
G.711 is an ITU-T-G.711 Recommendation (1988) pulse code modulation (PCM) logarithmic compression. The G.711 codec is an example of waveform-based compressing [URL (Cisco-coding)], which means that the decoder
reconstructs the actual signal without making an assumption on any speech models. G.711 is supported in PSTN, hardware interfaces for voice samples, and VoIP deployments. PCMU is PCM using aw, which is popularly used in North America. PCMA is PCM compression using the A-law scheme used in Europe and some countries of Asia. PCMA and PCMU together are called as G.711-based compression scheme. G.711 takes a smaller code size of the order of 100 lines, and processing is insignificant compared with other voice processing operations. The basic difference between PCMU and PCMA [URL (PCM), URL (TI-PCM)] schemes are actual quantization, coding steps, dynamic range, and bit formats. Some more details on G.711 and power-level calculations are given in the subsequent sections.
3.2.1
u-Law Compression of Analog Signal
In analog representation [Bellamy 11991) , URL (Cisco-coding), URL (TL PCM)] or for a continuous signal of |i-law compression, maximum input amplitude is mapped to normalized logarithmic output of ±1. For a given input x, the equation for |i-law encoding (compression) output y is given as follows:
![]()
In the equation, |i = 255 is the compression parameter, sgn(x) is the sign of x, sgn (positive number) = 1, and sgn (negative number) = -1. Symbol “ln” is the natural logarithm; i.e., logarithm to the base e = 2.71828. A natural logarithm is used in applications of finding unknown variables, Taylor series expansion, differentiation, and quantization. Logarithm to the base 10 is popularly used in power calculations. A | -law decoder (decompression) performs the reverse process of converting the compressed signal y back to the expanded analog signal X Expansion for the decoder input y is defined by the inverse equation
[Bellamy (1991), URL (TI- PCM) , URL (Cisco - coding) ].
![]()
Analog signals are usually represented as x(t), y(t), and X(t), with t as time. In the above equations, signals are denoted as x, y, and x for simplification in representation. In digital implementation, the linear input sample is converted to an 8-bit digital number after compression. Certain deviations of G.711 occur from continuous representation. Continuous representation gradually modifies step sizes, and G.711 follows finite segmented discrete steps.
3.2.2
PCMU for Digitized Signals
In G.711-based implementation, amplitude is split into eight segments for each polarity signal also called chords, and each segment has fixed quantization.
PCMU digital implementation takes a maximum linear sample sine wave amplitude of ±8159 equal to 3.17 dBm in power representation. The front-end analog circuit and ADCs are calibrated to take a 3.17-dBm sine wave and give ±8159 amplitude in digital number representation. The numbers 8159 and above are clipped to 8158 in the process of quantization. In the process of compression, the input range is broken into segments, and each segment will use different intervals. Most segments contain 16 intervals, and the interval size doubles from segment to segment as shown in Table 3.1. Large signals use a big quantization step and small signals use a small quantization step. This type of nonuniform quantization gives a signal-to-noise ratio (SNR) of 38 to 40 dB for most of the useful signal amplitude range and limits the significant signal dynamic range to 48 dB [Bellamy (1991)]. For full-scale amplitude of 3.17 dBm, signal to quantization is shown as 39.3 dB in reference [Bellamy (1991)].
A PCM 14 – bit (±8159 amplitude) input is split into eight amplitude segments represented with 3 bits. Each segment is quantized uniformly into 16 levels using 4 bits. The polarity of the input is represented using 1 bit. A sign bit is represented as “1″ for positive numbers and as “0″ for negative numbers. In a two’s complement number format, sign bit-1 is used for negative numbers. After framing 8 bits, the last 7 bits except the sign bit are inverted in PCMU.
This bit inversion increases the one’ s bit density in transmission systems that help timing and clock recovery circuits in the receiver. Ideal channel noise makes bits toggle between 01111111 (0x7F) and 11111111 (0xFF), which allows clock recovery to be better even under ideal channel conditions. Bit inversion is achieved by simple exclusive OR (XOR) operation of the encoded output with value 0x7F. This inversion is applied on both positive and negative values of input. At the decoder, the same operation of 7-bit inversion can retrieve the original decoded compressed byte. In Table 3.1, inverted encoder output is listed.
Interpretation of PCMU Coding. Table 3.1 lists PCMU encoded and decoded output values for positive and negative numbers. In the table, positive values are presented first for all segments, and negative values are given for a few segments to limit the table size. Higher amplitude is split into 16 equal intervals of 256 size and is categorized as segment number 81 but coded in 3 bits as “111,” which will occupy half (4063 to 8158) of the total amplitude. At the next level, 16 intervals of 128 are used, categorized as segment 7, and coded as “110,” which occupies one quarter (2015 to 4062) of the total range. The interval keeps decreasing by a factor of two, causing a small amplitude to be quantized with small quantization steps. The last column of Table 3.1 is the decoder
1PCMU has eight segments numbered from 1 to 8. The segment number and interval size of that segment are related as Interval size = 2lsegment number). In PCMU, the maximum interval size is 256, and the corresponding segment number is 8. However, encoded output has only 3 bits for representing the segment number, which means only numbers from 0 to 7 can be used for segment coding. Therefore, in PCMU, maximum and minimum segment numbers are coded as 111(7) and 000(0), respectively.
Table 3.1. PCMU Quantization Example for Positive Inputs and a Few Segments of Negative Inputs
| Decoder | |||||
| Output | |||||
| Segment | Interval | Step | Encoded Output After | for Input | |
| Input Range | in Bits | Size | Number | Bit Inversion | Range |
| 0 | 000 | 1 | 0 | 01111111(0x7F) 11111111(0xFF) | 0 |
| 1-2 | 000 | 2 | 1 | 11111110(0xFE) | 2 |
| 29-30 | 000 | 2 | 15 | 11110000(0xF0) | 30 |
| 31-34 | 001 | 4 | 0 | 11101111(0xEF) | 33 |
| 91-94 | 001 | 4 | 15 | 11100000(0xE0) | 93 |
| 95-102 | 010 | 8 | 0 | 11011111(0xDF) | 99 |
| 215-222 | 010 | 8 | 15 | 11010000(0xD0) | 219 |
| 223-238 | 011 | 16 | 0 | 11001111(0xCF) | 231 |
| 463-478 | 011 | 16 | 15 | 11000000(0xC0) | 471 |
| 479-510 | 100 | 32 | 0 | 10111111(0xBF) | 495 |
| 959 – 990 | 100 | 32 | 15 | 10110000(0xB0) | 975 |
| 991 – 1054 | 101 | 64 | 0 | 10101111(0xAF) | 1023 |
| 1951-2014 | 101 | 64 | 15 | 10100000(0xA0) | 1983 |
| 2015-2142 | 110 | 128 | 0 | 10011111(0x9F) | 2079 |
| 3935-4062 | 110 | 128 | 15 | 10010000(0×90) | 3999 |
| 4063-1318 | 111 | 256 | 0 | 10001111(0x8F) | 4191 |
| 7903-8158 | 111 | 256 | 15 | 10000000(0×80) | 8031 |
| For negative numbers, segments 0, 1, 6, and 7 are given to represent the beginning and the | |||||
| end of the range | |||||
| -1 to -2 | 000 | 2 | 1 | 01111110(0x7E) | -2 |
| -29 to -30 | 000 | 2 | 15 | 01110000(0×70) | -30 |
| -31 to -34 | 001 | 4 | 0 | 01101111(0x6F) | -33 |
| -91 to -94 | 001 | 4 | 15 | 01100000(0×60) | -93 |
| -2015 to -2142 | 110 | 128 | 0 | 00011111(0x1F) | -2079 |
| -3935 to -4062 | 110 | 128 | 15 | 00010000(0×10) | -3999 |
| -4063 to -4318 | 111 | 256 | 0 | 00001111(0x0F) | -4191 |
| -7903 to -8158 | 111 | 256 | 15 | 00000000(0×00) | -8031 |
output. For an input range of 7903 to 8158, output is one single value 8031. The value 8031 may be interpreted as the rounded mean value of the input range. To represent negative values, few selected ranges in the beginning and at the end are given.
3.2.3
PCMU Quantization Effects
Figure 3.1 has three graphs in three rows. The top graph is the encoder input and output relation for input values between 16 and 8158. The PCMU encoder output is given to the decoder, and the resulting absolute error is given in the middle graph. The middle graph shows a growing error with an increase in amplitude toward 8158. This error is happening because of the big step size at

Figure 3.1. PCMU quantization. (a) input and output relation indicating bigger steps at high amplitude. (b) error between input and corresponding decoder output — more error at high amplitude. (c) percentage of error with input — error is relatively steady for a wide range of input signal levels.
higher amplitudes. At lower amplitude, error is very low. In the middle graph, it can be observed that half of the amplitudes between 4063 and 8158 are occupied in 16 intervals, and it is continuing to reduce by a factor of 2 for lower input amplitudes. The bottom graph is the percentage of error or relative error with reference to the original input. As observed, error is contained to approximately ±3%. The percentage error is remaining steady with growing amplitude. It shows that relative distortion or signal to quantization or SNR caused by logarithmic compression will remain almost steady for a wide range of input amplitudes. At lower amplitudes from 0 to 16, the percentage of error is more and it increases toward an amplitude of “0.” In Table 3.1, for input-output relations of input “1,” the cascaded decoder output is 2. Error here is “1,” and percentage of error is 100%. In the bottom graph, it can be observed that percentage of error is growing toward an input amplitude of 16, which makes SNR caused by G.711 compression lower at lower amplitudes.
3.2.4
A-Law Compression for Analog Signals
In analog representation [ITU-T-G.711 (1988)] or a continuous signal of A-law compression, maximum input is mapped to a normalized logarithmic output of ±1. For a given input x, the equation for A-law encoding is defined by
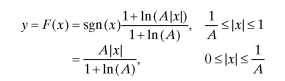
In the equations, x is the input to be compressed and A = 87.6 is the compression parameter. The A-law decoder performs a reverse process of expanding compressed samples to linear samples. A-law expansion is defined by a continuous inverse equation [Bellamy (1991), URL (TI-PCM)].
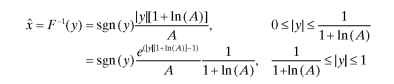
In digital implementation, a 16-bit linear input sample is converted to 8 bits after compression.
3.2.5
PCMA for Digitized Signals
PCMA takes a maximum input of ±4096 equal to 3.14dBm in power representation. The front – end analog circuit and analog – to – digital converters (ADCs) are calibrated to take 3.14 dBm and to give ±4096 amplitude in digital number representation. The quantization procedure is the same as with PCMU
with few deviations in quantization steps. The quantization steps of A-law use 4 bits for 16 quantization steps. The 16 intervals are of 128, 64, 32, 16, 8, 4, and
2 for two 16 intervals, which means the last two segments use the same interval 2. Of 16 total segments for positive and negative numbers, four segments from -63 to 63 use a step size of 2. Hence, PCMA is referred to as 13-segment quantization. PCMA encodes a 13-bit sample number to an 8-bit compressed sample. Similar to |>law, there are certain deviations of PCMA from continuous A–aw representation. Continuous representation gradually changes to step sizes. Table 3.2 shows A–aw compressed and expanded output for both positive and negative values as per G.711.
In PCMU, the last 7 bits are inverted, and in A–aw, encoder output even bits inversion (EBI) is used. In the A-law tables, bits before inversion and after EBI are also included in separate columns. EBI is performed in software by XOR operation of the encoded output with 0×55. EBI is applied on both positive and negative values of input. At the decoder, the same operation of even bit inversion can retrieve the original decoded compressed byte. EBI in PCMA once again helps clock recovery mechanisms during ideal channel or near zero amplitude signals.
3.2.6
PCMA Quantization Effects
In Fig. 3.2 , three graphs are given. This figure looks similar to Fig. 3.1 with PCMU, with the main difference in input range and quantization steps. The top graph is the input and output relation for input between 16 and 4096. The PCMA encoder output is given to the decoder, and the error is provided in the middle graph. The middle graph shows a growing error with an increase in amplitude toward 4096. At lower amplitude, the error is lower. In the middle graph, it can be observed that half of the amplitudes from 2048 to 4095 are occupying 16 intervals and that they are continuing to reduce by a factor of 2.
The bottom graph is the percentage of error or relative error with reference to the original input. Here error is contained to approximately ±3%. The percentage error remains steady with growing amplitude. This graph shows that relative distortion, signal to quantization, or SNR caused by logarithmic compression will remain almost steady at different amplitudes. At lower amplitude (0 to 16), the percentage of error is more, which makes the SNR lower at very small amplitudes.
3.2.7
Power Levels in PCMU/PCMA and SNR
PCMU maximum power is 3.17dBm for sine wave tone and corresponding input decimal numbers of ±8159. Any numbers above ±8158 are clipped to ±8158. For a square wave input of ±8158 or above, PCMU power is 6.17 dBm,
3 dB more than 3.17dBm. A sine wave or perfect square wave may be used for calibration purposes. In actual measurements, a square wave test may not
Table 3.2. PCMA Quantization Example for Positive Inputs and a Few Segments of Negative Inputs
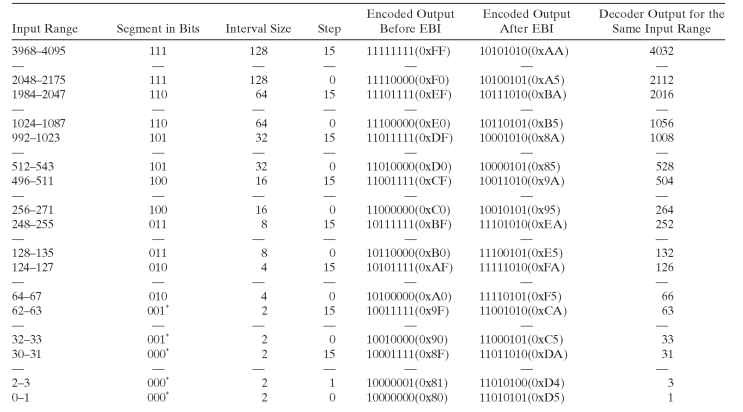
Table 3.2. Continued
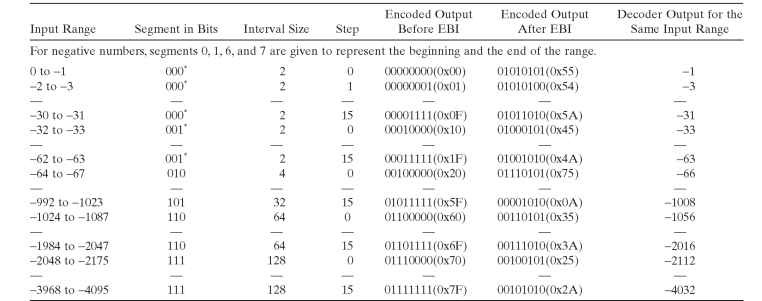
*Note: In the G.711 recommendation, the last segment is shown as a long segment with 32 values. Here it is shown as segment 1, but a segment field in the segment position of 8 bits was changed to “000.” In actual coding, this results in a 3-bit segment value of “000.” To avoid confusion, in this section, it is listed as “0″ in the segment column instead of “1.” It has to be noted that the interval is 2 for segments 0 and 1. The modified values are used in Table 3.2 for the last segment. While referring to multiple references, the difference in representation has to be noted.

Figure 3.2. PCMA quantization: (a) input and output relation indicating bigger steps at high amplitude, (b) error between input and corresponding decoder output — more error at high amplitude, and (c) percentage of error with input — error is relatively steady for a wide range of input signal levels.
be used and is not accurate. The front-end telephone interfaces limit the square wave bandwidth, which causes rise and fall of the square wave. Hence, the measurements will not match with the mathematical representation of a square wave. In general, telephone measuring instruments use sine wave tone and a combination of sine wave tones for the tests.
In PCMA, maximum sine wave power is 3.14 dBm. For a square wave, this is 6.14dBm. The same interpretation of PCMU is applicable for PCMA for amplitude limits at ±4096. The SNR of the PCMU and PCMA are in the range of 38 to 40dB [URL (PCM)] . The SNR of PCMU is estimated as 39.3dB [Bellamy (1991)] for a full-scale sine wave of 8159. The SNR varies based on the signal amplitude. To conduct measurements for the SNR or power-l evel
calibration sine wave, a range of 1004 to 1020 Hz is used. The details on the acceptable SNR for different signal levels are given in TR-57 (1993). A tone of 1004 Hz is not harmonically related to 8000 Hz, and it exercises all encoder and decoder levels [Bellamy (1991)].
The quality difference between PCMU and PCMA is minor in nature. PCMA has a higher dynamic range, but PCMU signal quality is better than PCMA. For small signals, PCMA works as 2/4096 quantization, and PCMU is 2/8159; therefore, the signal quality from PCMU is better. Ideal channel noise is quantized better in PCMU. PCMA does not define zero-level output for the first quantization interval; hence, PCMA is a mid-riser quantizer. The quality degradation with this type of quantization difference is imperceptible [Bellamy
(1991) ].
