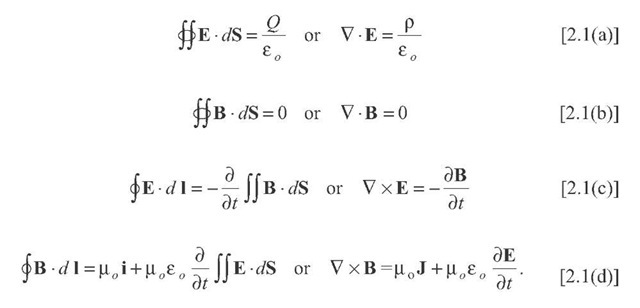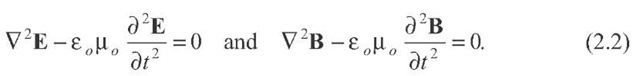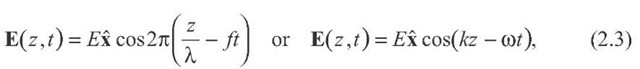We have discussed various remote sensing modalities and some characteristics of modern systems; at this point, it is necessary to review some basic physics.
The chief thing to understand is the electromagnetic (EM) spectrum and EM radiation, of which light, radar, and radio waves are examples. We’ll look at the physical equations that underlie EM waves, the wave equations that result, their energy in the context of the photoelectric effect, sources of EM radiation, and some fundamental interactions of EM waves with matter.
Maxwell’s equations
The principles that define electricity and magnetism were codified by Maxwell in the late 1800s in four equations that bear his name:
These four equations, respectively, say the following:
a) The electric flux through a Gaussian surface is equal to the charge contained inside the surface.
b) In the absence of a magnetic point charge, the magnetic flux through a Gaussian surface is equal to zero.
c) The voltage induced in a wire loop is defined by the rate of change of the magnetic flux through that loop (the equation that defines electrical generators).
d) A magnetic field is generated by a current (typically in a wire), but also by a time-varying electric field.
These equations can be manipulated in differential form to produce a new differential inline equation, the wave equation in either electric or magnetic fields:
Maxwell understood that the solutions to these equations were defined by oscillating electric and magnetic fields (E and B). In particular, these equations immediately give the speed of light:
. The complexity of the solutions vary, but there are some fairly simple ones involving plane waves propagating in a straight line. Like all wave phenomena, the solution involves the wavelength, frequency, and velocity of the radiation. In equation form, a typical solution looks like this:
which is the equation for a wave propagating in the plus z direction, with an electric field polarized in the x direction (more on polarization below). The various terms in this equation are defined as follows:
E = amplitude of the electric field
= wavelength (in m) f = frequency in Hz (cycles/s) c = phase velocity of the wave (in m/s)
= angular frequency,
k = the wave number,
The solution depends upon the wavelength and frequency, which are related by:
Figure 2.1 Four cycles of a wave are shown, with wavelength X, or period t. The wave has an amplitude A equal to 3.
For EM waves in a vacuum, the value of
an important constant of physics. Note that the period t is the inverse of the frequency, because for a wave it must be true that
The angular frequency and wave number are somewhat less intuitive than the frequency and wavelength, but are standard terminology in describing waves.
