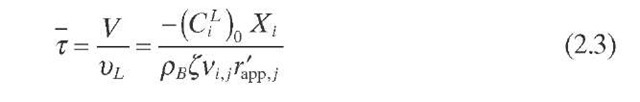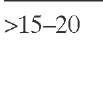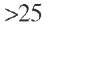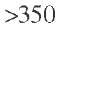Ideal Flow Reactors
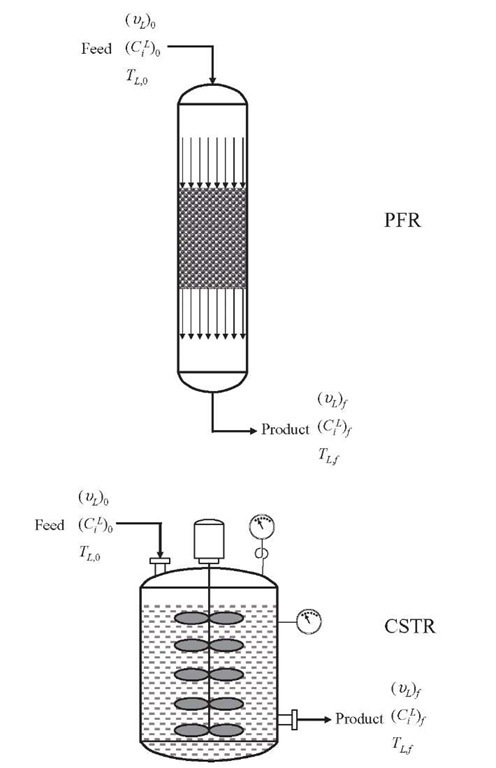
Plug – flow and perfectly mixed patterns are the two ideal extremes in which continuous reactors commonly lie (Figure 2.5). The ideality of these two flow patterns allows simple mathematical description of the reactors, and reliable and easy treatment of experimental data since radial and axial mass and heat dispersion terms in the continuity equations are neglected. Macro gradients of concentration or temperature in the reactor are the major reasons for deviations from ideal flow patterns, which may result from imperfect mixing in the case of CSTR or from axial dispersion, wall effects, or catalyst bypassing in the case of a plug-flow reactor (PFR). These intrareactor gradients affect the evolution of the chemical reactions occurring inside. Therefore, they have to be taken into account to avoid errors during experimental data interpretation.
Figure 2.5. Ideal flow patterns.
Following are some observations about deviation from ideal plug flow in TBRs:
• Axial liquid dispersion in commercial reactors is not significant relative to the bulk flow.
• Reduction of reactor bed length will cause greater deviation from plug flow than will reduction of reactor bed diameter.
• Wall flow leads to axial dispersion because of higher fluxes in the area near the wall, where the packing void fraction is higher.
Once the criteria for elimination of intrareactor transport effects are fulfilled, the substitution of new catalyst and/or feedstocks in existing TBRs can also be studied with considerably scaled- down reactors. The way in which laboratory and bench-scale reactors have to be operated to ensure the ideality of flow pattern for measuring intrinsic reaction rates is described in the following sections.
Plug-Flow Continuous Reactor The mass balance equation for any flow pattern is given by
DaL and DrL are the overall axial and radial dispersions in the liquid phase, respectively, which are made up of contributions from axial molecular diffusion, convective dispersion in the packing, and macroscopic velocity distributions in the reactor. When the reacting fluid moves through the PBR in turbulent flow, the fluid moves like a plug or piston. In the PFR, the condition of turbulent flow generally ensures the absence of concentration, temperature, and velocity gradients in the radial direction, that is, well-mixed radially and zero – mixed axially (Perego and Paratello, 1999). Hence, the space-rime (t) expression from the steady-state mass balance equation for ideal plug flow in PBR becomes
A plug – flow regime implies that the residence time of each volume element of the fluid must be the same as that in a large number of mixers in series. Hence, axial molecular diffusion may be the main cause of spread in the residence time in the reactor; meanwhile, the axial convective dispersion within the packing results from statistical variations in the width, length, and direction of individual channels (Sie, 1996).
-f a commercial TBR is assumed to be close to an ideal integral FBR, although the hydrodynamics is different, the condition for a kinetically representative laboratory reactor is that it should also be sufficiently approximate to ideality behavior. A well-designed industrial FBR can be considered as a close approximation to an ideal integral reactor if the following criteria are fulfilled (Sie, 1996):
• All volume elements of the feed must last the same time inside the reactor so as to contribute equally to the overall conversion (e.g., PFR behavior, narrow residence time distribution of the liquid).
• All parts of the catalyst bed must contribute maximally to the overall conversion (all catalyst particles in good contact with the reactant stream, i.e., complete contacting of the catalyst with the liquid phase).
Therefore, hydrodynamics in laboratory and pilot-plant reactors is of importance only to the extent that they affect compliance with the following requirements: plug – flow pattern, complete catalyst particles wetting, pressure drops, and heat transport phenomena.
Perfectly Mixed Continuous Reactor Perfectly mixed reactors include an external recycle reactor (recycle-to-feed flow ratio > 25) and a CSTR. On the macroreactor scale, both types of reactors are characterized by the absence of intrareactor concentration and temperature gradients throughout the reaction volume. According to the ideal behavior, the space-time may be obtained directly from a simple algebraic equation expressed in terms of effluent conversion:
Intrareactor Temperature Gradients
Temperature differences inside a reactor may originate from mass and temperature intrareactor gradients, which can cause deviations from isothermality. Uniformity of reactor temperature profile is a crucial characteristic for performing appropriate experiments in order to obtain intrinsic reaction rates, since it is very difficult to cope up with intrinsic rate constants from noniso-thermal data. Therefore, both axial and radial gradients must be minimized. Due to the exothermic or endothermic nature of reactions, axial temperature gradients in FBRs are always present; however, by increasing the ratio of bed length to catalyst particle diameter (LB/dpe) the gradients can be minimized. Dilution of either the feed or the catalyst and decreasing the reactor diameter are the most common experimental methods for reducing radial temperature gradients. If the reactor diameter is decreased, the particle diameter should also be reduced, to maintain a constant dR/dpe ratio and fulfill the PFR condition without introducing flow bypassing problems. However, dilution of catalyst particles with smaller inert particles produces high pressure drops. This problem can be solved by mixing catalyst particles with suitably sized inert particles so that good fluid distribution and low pressure drop are guaranteed.
The mathematical criteria reported in the literature to neglect temperature gradients generally compare two functions, one representing measurable parameters of the actual system and the other calculated from theoretical parameters. If the value of the former is greater (or lower) than that of the latter, it is assumed that the temperature gradient observed may cause only a certain deviation (e.g., a 5 or 10% difference in reaction rate).
Radial Heat Dispersion Radial and axial transport effects within a reactor are not easy to evaluate and control. Radial temperature gradients probably cause unreliable data in TBRs, which are attributed to heat conduction problems due to low effective thermal conductivity of the catalyst. When the reaction rate and heat release are large, severe radial temperature gradients are expected. If these gradients are neglected, they can lead to reaction rates several orders of magnitude greater than those calculated with the temperature at the wall, thus causing unreliable results in PFRs (Mears, 1971).
Typical diameters of experimental reactors (e.g., pilot scale and bench scale) may provoke undesired radial temperature profiles if the reactor is not operated in true adiabatic mode. It has been shown that in these experimental reactors, radial heat transfer effects at the hot-spot location are more important than axial heat transfer effects (Mears, 1976). These intrareactor temperature gradients are nearly always more severe than interphase temperature gradients, which are generally more severe than intraparticle temperature gradients. Therefore, isothermal operation of the reactor is critical to the generation of reliable laboratory data. For this task, mathematical criteria aid in understanding what reactor system features can be manipulated to achieve better isothermal control. Based on this, the following recommendations can help to establish isothermal operation:
• Low conversion levels
• Small catalyst particles
• Dilution of catalyst bed with inert particles to decrease bed voidage
• High thermal conductivity catalyst support
• Feed diluents with high thermal conductivity
• High flow rates
• Decreased reactor diameter
Mears (1971) has pointed out the importance of decreasing the diameters of both the reactor and the catalyst particles to minimize radial interparticle heat transport limitations in experimental FBRs with heat exchange at the wall. However, this may not be appropriate to avoid the wall effect. The approximate criterion derived by Mears (1971) for determining the existence of radial interparticle heat transfer limitations often causes severe deviations from the isothermal plug- flow operation desired. Mears (1971) established that <5% deviation in the reaction rate due to radial temperature gradients for high values of dR/dpe (>100), where heat transfer resistance at the wall of the reactor is negligible, is found if Eq. (2.4) (Table 2.1) is fulfilled. However, for small laboratory reactors, heat transfer resistance at the wall cannot be neglected. If it is significant, for such a deviation in the reaction rate in cases when dR/dpe < 100, the interparticle criterion becomes Eq. (2.5). This criterion is conservative when applied at the inlet section of a reactor, but it does apply at any cross section in reactors with linearly decreasing dilution, and at the hot spot in undiluted or uniformly diluted beds.
TABLE 2.1. Equations for the Criteria for Intrareactor Temperature Gradients
|
Criterion |
Eq. |
 |
(2.4) |
 |
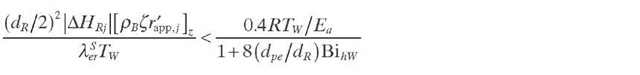(2.5) |
 |
(2.6) |
 |
(2.7) |
 |
(2.8) |
Doraiswamy and Tajbl (1974) have indicated that a reduction in reactor diameter, and thus in the aspect ratio (dR/dpe), is helpful in minimizing radial temperature gradients. The practical lower limit of dR/dpe appears to be about 4, so the contribution of heat transfer at the inside tube wall is not significant. According to Butt and Weekman (1974), the critical design factor to avoid the influence of radial temperature gradients is reactor diameter and hence the dR/dpe ratio, since if the reactor diameter is reduced beyond a limit, the wall effect will appear. There are not analytical criteria to choose the dR/dpe ratio. However, most researchers have reported values between 10 and 20. Once this ratio has been specified, the criteria given by Eqs. (2.4) and (2.5) may be used to estimate the probable influence of radial temperature gradients.
Carberry (1976) stated that a reactor diameter of five to six times the particle diameter is the maximum value at which reactor isothermality is certain to be maintained. However, this criterion is in conflict with the general PBR rule that a minimum of 8 to 15 particle diameters is necessary to minimize wall effects. This means that no matter what is done invariably, some error will be made (Tarhan, 1983). Although the catalyst bed will be diluted with a good heat-conducting material [e.g., silicon carbide (SiC), «-Al2O3, or quartz], it is recommended that temperatures at the wall and at the center of the bed always be measured if the reactor diameter is greater than 3 cm (Gierman, 1988).
Axial Heat Dispersion The sensible heat term can be neglected in the differential energy balance when the axial temperature gradient is zero. This occurs at any cross section in reactors with linearly decreasing dilution and at hot-spot locations. Axial heat conduction can also be neglected for beds with a sufficient length-to-particle diameter ratio (LB/dpe > 30), so that plug flow is approached.
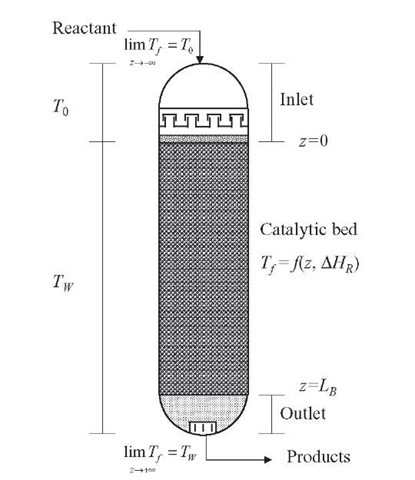
Young and Finlayson (1973) proposed the criterion given by Eq. (2.6) to neglect axial heat dispersion at the initial reactor section without catalyst particles. If Eq. (2.6) [and Eq. (2.4) for axial mass dispersion] is not properly satisfied, axial mass and heat dispersions will be important at the inlet section of the reactor, although axial dispersion may be of less or no importance at the outlet. Neglecting these axial dispersion effects would lead to errors at the inlet, and consequently, in the entire reactor. Young and Finlayson (1973) also proposed another criterion [Eq. (2.7)] to determine the importance of axial heat dispersion in the reactor section with catalyst particles. Based on the criterion proposed by Young and Finlayson (1973), Mears (1976) derived another criterion [Eq. (2.8)] to consider cases where the inlet reactor temperature is equal to the wall reactor temperature (T ,0 = TW) or for endothermic reactions (Figure 2.6 ).
Intrareactor Mass Gradients
Radial Mass Dispersion Compared with other hydrodynamic parameters, relatively few studies have been reported on the radial liquid distribution in TBRs. The reactor-to-particle size ratio (dR/dpe- has been demonstrated to have a significant effect on radial distribution (Saroha et al., 1988). In large commercial units, a uniform radial mass can be achieved by employing a suitable design for a multipoint distributor and other reactor internals (Alvarez et al., 2007). In laboratory reactors, a single -point distributor and a certain amount of inert material (e.g., a helly pack) are generally used to achieve a prior uniform radial distribution. An adequate radial flow of reactants and products through the catalyst beds can minimize the pressure drop in FBRs.
Bischoff and Levenspiel (1962) have presented a criterion [Eq. (2.9), Table 2.2] to neglect the radial dispersion effect in packed beds based on the ratio of the catalytic bed length to the reactor diameter. For large ratios of reactor to particle diameter (dR/dpe > 25), D^ is approximately constant over the radius in packed beds. By assuming a size of one particle diameter for individual stirred tanks, Levenspiel and Bischoff (1963) found that eLDrL / uLdpe = 0.21 for flow in packed beds with a Reynolds number higher than 100. Satterfield (1970) confirmed that liquid and gas radial dispersion is constant for a particle Reynolds number (Re) higher than 100, whereas axial dispersion is constant for Re > 10. According to Carberry and White (1969)- the product yield calculated for an FBR using a two-dimensional model is quite sensitive to a radial heat transport effect but is virtually insensitive to a radial mass transport effect. This suggests that if a reactor design meets the criteria for eliminating a radial temperature gradient, the radial mass transport effect can be neglected by assuming uniform radial concentration.
Figure 2.6. Geometry of a nonisothermal reactor to derive the criterion of Young and Finlayson (1973).
Axial Mass Dispersion Contrary to radial mass dispersion, mass transfer in the axial direction is always present, but it can be minimized to prevent significant deviations from plug flow by selecting the appropriate ratio of bed length to particle diameter (LB/dpe). Table 2.3 summarizes the values of this ratio proposed by different researchers for neglecting axial mass dispersion. The axial dispersion of the reactant in an FBR can also be described in terms of an equivalent number of CSTR in series (N) or by the dimensionless Peclet number (Pe) defined by Eq. (2.10) – in which the reactor length (LB) features as the characteristic dimension. For axial dispersion caused only by packing, the dimensionless Bodenstein number (Bo), defined by Eq. (2.11), can be used to describe it; in this case the equivalent particle diameter (dpe) is chosen as the characteristic dimension. In Eqs. (2.10) and (2.11), Dfa is the overall axial-dispersion coefficient, which includes contributions from axial molecular diffusion, convective dispersion in the packing, and macroscopic velocity distributions in the reactor (Sie, 1996). By combining these two equations, the relationship given by Eq. (2.12) between the Peclet and Bodenstein numbers can be derived.
As a general criterion, to have ideal plug-flow behavior, N or Pe should be higher than a certain minimum value. This minimum value depends on the reaction order (n) and the degree of conversion (X). The minimum Peclet number is about twice the equivalent number of CSTRs in series [Eq. (2.13)]. Based on a variety of published data of axial dispersion in fixed beds for trickle flow, Gierman (1988) developed a correlation between Bodenstein and liquid particle Reynolds numbers which shows that an increased Bo number requires an increased Re number when Re > 10. However, the Bo number reaches a more or less constant value at low Re numbers, which are typically found in small laboratory reactors (0.001 < Re < 0.1). This is valid for single-phase flow as well as for trickle flow with a lower constant value of Bo for trickle flow, indicating greater axial dispersion in a trickle bed at similar velocity and particle size. The mean Bodenstein value for the low Reynolds region of interest in laboratory TBRs is 0.04.
Szekely (1961) and Petersen (1965) applied an asymptotic solution approach to isothermal first-order reactions and found that the effect of backmixing is negligible ( LBPILB ~ 1) if the reaction rate is slow. They proposed the criterion given by Eq. (2.14) for plug flow. Mears (1971) obtained a more conservative design criterion by utilizing perturbation solutions for power-law kinetics, which holds the deviation in the required reactor length to less than 5% [Eq. (2.15)]. This criterion shows that the dispersion effect can be negligible except for cases involving short beds and high conversion.
Levenspiel and Bischoff (1963) developed a criterion to neglect deviations from plug flow in isothermal reactors with first – order reactions. They proposed Eqs. (2.16) and (2.17), which involve conversion and size of the actual reactor and the reactor calculated using the plug-flow model. By combining Eqs. (2.11) and (2.17) and assuming the mean residence time of fluid in the system (t) with a maximum error of 5%, Eqs. (2.18) and (2.19) in terms of concentration and conversion can be obtained. This criterion is best suited for design purposes and might not be valid for large eLD^ /(uLLB) values (Young and Finlayson, 1973). By taking the size of an individual CSTR equal to one particle diameter, the value eLDL / uLdpe = 0.5 can be reproduced for flow in packed beds with Re > 100 (Satterfield, 1970).
For a 4% deviation of plug flow in adiabatic reactors with single nth - order reactions, Hlavacek and Marek (1966) proposed the criteria given by Eqs. (2.20) and (2.21). One of the most used design criteria based on the minimum bed length required to neglect axial dispersion or backmixing effects on three-phase reactor behavior was developed by Mears (1971) , who was the first to use a relationship between Bo number, reaction order n , and conversion X. . The criterion establishes that deviation in the required actual reactor length with respect to the ideal length where plug flow is achieved (for a given conversion) is less than 5% if Eq. (2.22) is fulfilled.
TABLE 2.2. Equations for the Criteria for Intrareactor Mass Gradients
|
Criterion |
Eq. |
Criterion |
Eq. |
 |
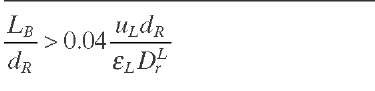(2.9) |
 |
(2.16) |
 |
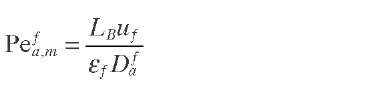(2.10) |
 |
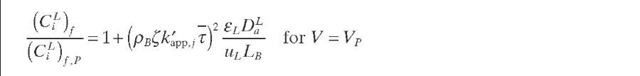(2.17) |
 |
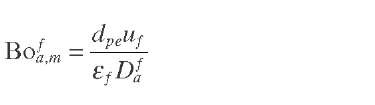(2.11) |
 |
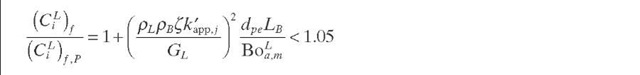(2.18) |
 |
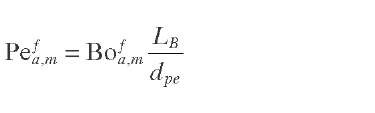(2.12) |
 |
(2.19) |
 |
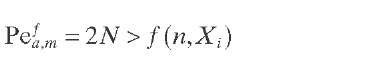(2.13) |
 |
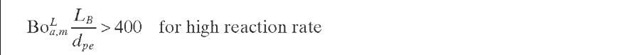(2.20) |
 |
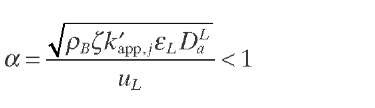(2.14) |
 |
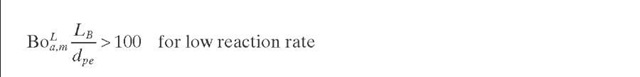(2.21) |
 |
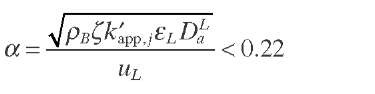(2.15) |
 |
(2.22) |
 |
 |
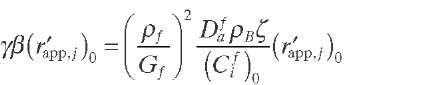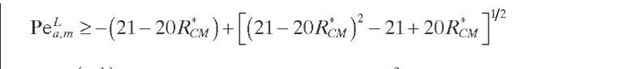(2.29) |
|
 |
(2.23) |
 |
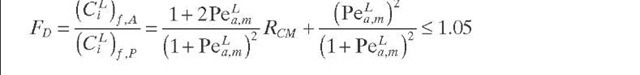(2.30) |
 |
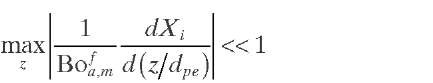(2.24) |
 |
( 2.31) |
 |
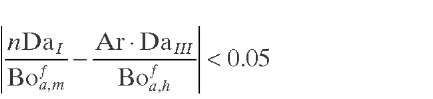(2.25) |
 |
(2.32) |
 |
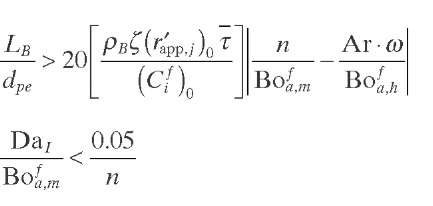(2.26) (2.27) |
 |
(2.33) (2.34) |
 |
(2.28) |
 |
TABLE 2.3. Rule of Thumb for Axial Mass Dispersion
 |
Application |
Reference |
 |
From data of Hochman and Effron (1969) on TBR with a liquid mass velocity of 4 kg/m2-s |
Gianetto and Specchia (1992) |
 |
To minimize axial dispersion in packed towers |
Scott (1935) |
 |
Simple rule of minimum length to neglect axial mass dispersion and heat conduction |
Mears (1971) |
 |
Axial dispersion and axial heat conduction can be neglected, ensuring that plug flow is closely approached |
Doraiswamy and Tajbl (1974) |
 |
For long isothermal reactors |
Carberry and Wendel (1963) |
 |
For the flow velocities in industrial practice the effect of axial dispersion of heat and mass on conversion is negligible |
Froment and Bischoff (1990) |
 |
For two – phase FBRs |
Perego and Paratello (1999) |
 |
For neglecting backmixing effects in two-phase FBRs |
Ancheyta et al. (2002) |
 |
For TBRs |
Perego and Paratello (1999) |
 |
To avoid backmixing in TBRs |
Sie (1991) |
 |
Minimum axial dispersion for bench-scale HDT units processing straight-run gas oil |
Mears (1971,1974) |
 |
Backmixing is minimum |
Kumar et al. (2001) |
Equation (2.22) was derived from perturbation solutions using the one -parameter piston diffusion (PD) model for power-law kinetics. Its applicability is valid only under the conditions of liquid- l imiting reactions (it cannot be applied to complete external wetting), nth-order irreversible reaction kinetics, isothermal TBR, and conversion of less than 90%. The minimum length for negligible deviation increases with an increase in conversion or a decrease in Bodenstein number. As Mears (1971) pointed out, no simple rules such as LB/dpe > 30 are adequate for all cases.
Young and Finlayson (1973) examined the importance of both axial and radial dispersion in nonadiabatic reactors. A criterion was derived [Eq. (2.23)] (Figure 2.6) to determine if axial mass dispersion is important at the inlet section of nonisothermal PBRs with cooling or heating at the walls and with inlet and outlet sections free of catalyst particles. Even though criteria for axial heat dispersion [Eq. (2.6)] and axial mass dispersion [Eq. (2.23)] are satisfied, if the maximum axial temperature or conversion gradient occurs at z ^ 0, discrepancies in temperature and conversion profiles from those with plug flow can also occur. An indication of the importance of axial dispersion inside the reactor can be obtained by comparing the fluxes with and without axial dispersion. If axial mass dispersion is to be negligible, the absolute difference in the fluxes for these two cases must also be negligible [Eq. (2.24)]. The problem with using the criteria for axial heat dispersion [Eq. (2.7)] and axial mass dispersion [Eq. (2.24)] is that their importance inside the reactor requires knowledge of the maximum temperature and conversion gradients.
Shah and Paraskos (1975) extended Mears’ (1971) criterion for isothermal TBRs to predict significant axial dispersion effects in commercial and pilot-scale adiabatic hydroprocessing TBRs. The criteria were validated for irreversible reactions following power-law kinetics (n = 1 and 2) and BoLm > 3. It was observed that at high conversions, adiabatic operation produces a larger axial dispersion effect than that produced by isothermal operation. At low conversions, the opposite results were obtained. Plots of (PeLm ) in the plane of Pe£m versus R’n for first- and second-order reactions were used to show the criteria for Lb = 0.95Lbp. For vapor-phase reactors, these criteria do not apply in cases where the external film heat transfer is important.
Mears (1976) applied the inlet rate criterion proposed by Young and Finlayson (1973) to evaluate the axial dispersion effect of heat and mass in an nonisothermal reactor cooled or heated at the wall, with a uniform temperature along the wall reactor [Eq. (2.25)]. This criterion predicts that the reaction rate deviation from plug-flow conditions at the reactor inlet will be less than ±5%. It is more precise and less conservative than the criteria given by Eqs. (2.6) and (2.23). The criterion may also be expressed in terms of minimum length for insignificant axial dispersion effect at the inlet section [Eq. (2.26)]. From a criterion expressed in this way, it is possible to see that the minimum length increases with increases in conversion, reaction order, heat of reaction, and activation energy for the specific case of isothermal reactors with first-order reactions throughout the bed and non-first-order reactions at the inlet section before the catalyst bed [Eq. (2.27)].
Mears’ (1971) conservative criterion to neglect axial dispersion effects on TBRs was slightly modified by Gierman (1988). The former is attained to estimate concentration deviation values from plug flow of less than 5%; the latter, for deviations less than 10%. Gierman’s criterion is based on the more relaxed criterion that the temperature requirement for the same conversion should not be higher than theoretical by about 1°C, which is considered to be the maximum accuracy of temperature definition in practical cases. For the usual magnitude of activation energy of reactions of interest, the criterion proposed is that given by Eq. (2.28) (Sie, 1996).
Both Mears and Gierman criteria apply only for liquid–imiting reactions. According to the authors, much higher LB/dpe ratios are required in laboratory experiments than those expected from the rule of thumb of LB/dpe > 50. For FBRs, the latter simple criterion is indeed sufficient, provided that the particle Reynolds number is above 10. However, laboratory reactors are usually operated with a particle ReL < 0.1 being more the rule than the exception.
Cassanello et al. (1994) demonstrated that Mears’ model is severe only in certain conditions and formulated another criterion for liquid or gaseous limited reactions, based on a general approximation to the solution of the axial dispersion model, to establish the conditions under which the liquid axial dispersion affects the behavior of three-phase FBRs for both downflow and upflow operations [Eq. (2.29)]. This criterion implies that the deviation with respect to the plug-flow model should not be larger than 5%.
Cassanello et al. (1996) developed a general criterion to analyze the influence of plug-flow deviations on TBRs – behavior. The criterion may be used for reactor design purposes by determining operating conditions and geometric features to ensure negligible axial dispersion effects based on the assumption that deviations with respect to the plug-flow model should not be larger than 5% if Eq. (2.30) is fulfilled. By applying a general approximate solution of the axial dispersion model and considering the ratio of product concentrations, Eq. (2.30) can be expressed as Eq. (2.31) – This criterion is valid for any type of kinetics and very useful when the geometrical characteristics and operating conditions of the reactor are already defined. However, the kinetic constant is unknown. Similar to the criterion developed by Cassanello et al. (1992) – for this critical Peclet value, deviation of outlet concentration with respect to that from plug flow is close to 0.95. The main disadvantage of this criterion is the need of reactant concentration at the reactor outlet according to perfect mixing (PeL,m ^ 0) and plug-flow ( PeL,m ^ models. However, the evaluation of these concentrations is much easier than that corresponding to the axial dispersion model.
It is possible to evaluate PeL,m from correlations reported in the literature and to measure the reactant outlet concentration. If the experimental outlet concentration is considered as that obtained by assuming a plug-flow model, the apparent kinetic constant can be estimated in a first approximation. The value obtained in this way is used to calculate the outlet concentration with the perfect mixing model. Hence, the ratio given by Eq. (2.32) is determined, which can be applied in Eq. (2.30) to estimate whether there is an axial dispersion effect in the experimental measurements.
From data of Hochman and Effron (1969) on TBRs with a liquid mass velocity of 4kg/(m2-s), Gianetto and Specchia (1992) established that plug flow should be approximated in beds in which LB/dpe > 15 to 20. For kinetic experiments at high conversion, van Herk et al. (2005) indicated that the Peclet number is a more suitable parameter to be considered and proposed the rule of thumb given by Eq. (2.33) for neglecting axial mass dispersion. Since achieving the criteria proposed by Mears (1971) and Gierman (1988) might still be too strict for some cases [e.g., hydrotreating TBR when producing ultralow-sulfur diesel due to the very high conversions (99.5% or even higher)], Chen et al. (2009) have proposed an even more relaxed criterion with 15% deviation from plug flow [Eq. (2.34) ].
