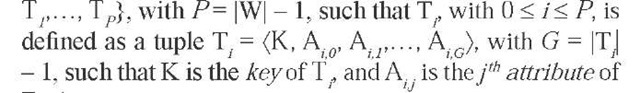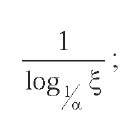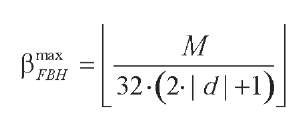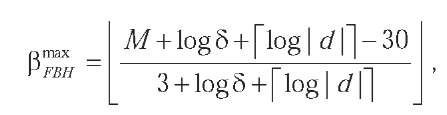Introduction
Histograms have been extensively studied and applied in the context of Selectivity Estimation (Kooi, 1980; Muralikrishna & DeWitt, 1998; Piatetsky-Shapiro et al., 1984; Poosala et al., 1996; Poosala, 1997), and are effectively implemented in commercial systems (e.g., Oracle Database, IBM DB2 Universal Database, Microsoft SQL Server) to query optimization purposes. In statistical databases (Malvestuto, 1993; Shoshani, 1997), histograms represent a method for approximating probability distributions. They have also been used in data mining activities, intrusion detection systems, scientific databases, that is, in all those applications which (i) operate on huge numbers of detailed records, (ii) extract useful knowledge only from condensed information consisting of summary data, (iii) but are not usually concerned with detailed information. Indeed, histograms can reach a surprising efficiency and effectiveness in approximating the actual distributions of data starting from summarized information. This has led the research community to investigate the use of histograms in the fields of database management systems (Acharya et al., 1999; Bruno et al., 2001; Gunopulos et al., 2000; Ioannidis & Poosala, 1999; Kooi, 1980; Muralikrishna & DeWitt, 1998; Piatetsky-Shapiro et al., 1984; Poosala, 1997; Poosala & Ioannidis, 1997), online analytical processing (OLAP) systems (Buccafurri et al., 2003; Cuzzocrea, 2005a; Cuzzocrea & Wang, 2007; Furfaro et al., 2005; Poosala & Ganti, 1999), and data stream management systems (Guha et al., 2001; Guha et al., 2002; Thaper et al., 2002), where, specifically, compressing data is mandatory in order to obtain fast answers and manage the endless arrival of new information, as no bound can be given to the amount of information which can be received.
Histograms are data structures obtained by partitioning a data distribution (or, equally, a data domain) into a number of mutually disjoint blocks, called buckets, and then storing, for each bucket, some aggregate information of the corresponding range of values, like the sum of values in that range (i.e., applying the SQL aggregate operator SUM), or the number of occurrences (i.e., applying the SQL aggregate operator COUNT), such that this information retains a certain “summarizing content.”
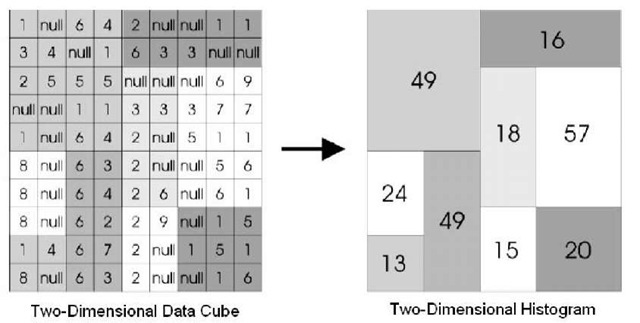
Figure 1 shows an instance of a histogram built on a two-dimensional data cube (left-side of the figure), represented as a matrix. The corresponding (two-dimensional) histogram (right-side of the figure) is obtained by (i) partitioning the matrix into some rectangular buckets which do not overlap, and (ii) storing for each so-obtained bucket the sum of the measure attributes it contains.
Histograms are widely used to support two kinds of applications: (i) selectivity estimation inside Query Optimizers of DBMS, as highlighted before, and (ii) approximate query answering against databases and data cubes. In the former case, the data distribution to be compressed consists of the frequencies of values of attributes in a relation (it should be noted that, in this vest, histograms are mainly used within the core layer of DBMS, thus dealing with databases properly). In the latter case, the data distribution to be compressed consists of the data items of the target domain (i.e., a database or a data cube) directly, and the goal is to provide fast and approximate answers to resource-intensive queries instead of waiting-for time-consuming exact evaluations of queries. To this end, a widely-accepted idea is that of evaluating (with some approximation) queries against synopsis data structures (i.e., succinct, compressed representations of original data) computed over input data structures (i.e., a database or a data cube) instead of the same input data structures. Histograms are a very-popular class of synopsis data structures, so that they have been extensively used in the context of approximate query answering techniques. Some relevant experiences concerning this utilization of histograms are represented by the work of Ioannidis and Poosala (Ioannidis & Poosala, 1999), that propose using histograms to provide approximate answers to set-valued queries, and the work of Poosala and Ganti (Poosala & Ganti, 1999), that propose using histograms to provide approximate answers to range-queries (Ho et al., 1997) in OLAP.
In both utilizations, a relevant problem is how to reconstruct the original data distribution form the compressed one. In turn, this derives from the fact that the original data distribution summarized within a bucket cannot be reconstructed exactly, but can be approximated using some estimation strategies, like continuous value assumption (CVA) (Colliat, 1996) or uniform spread assumption (USA) (Poosala et al., 1996). For a given storage space reduction, the problem of determining the “best” histogram (i.e., the histogram which minimizes the approximation of reconstructing the original content of ranges corresponding to buckets) is crucial. Indeed, different partitions lead to dramatically different errors in reconstructing the original data distribution, especially for skewed (i.e., asymmetric) data. This issue has been investigated for some decades, and a large number of techniques for arranging histograms have been proposed (Buccafurri et al., 2003; Christodoulakis, 1984; Donjerkovic et al., 1999; Ioannidis & Poosala, 1995; Jagadish et al., 2001). The aim of every partition technique is to build a histogram whose buckets contain values with “small” differences, so that one can estimate a range query inside a bucket assuming that data distribution is uniform, thus successfully exploiting linear interpolation. Indeed, finding the optimal solution to this problem in multiple dimensions is NP-hard (Muthukrishnan et al., 1999). Several techniques and heuristics have been proposed to find sub-optimal solutions with provable quality guarantees (Jagadish et al., 1998; Gilbert et al., 2001). These guarantees regard the “distance” of the provided solution from the optimal one, but do not provide any measure of the approximation of each estimated answer to a range-query.
Figure 1. A two-dimensional data cube and its corresponding two-dimensional histogram
Another important, more recent utilization of histograms concerns with the data visualization problem, where the data compression paradigm is intended as a solution to aid the visualization of complex and multidimensional domains. This is a quite-unexplored line of research: pioneeristic works can be found in the DIVE-ON (Ammoura et al., 2001) and Polaris (Stolte et al., 2002) projects, whereas recent works can be found in (Cuzzocrea et al., 2007).
In this chapter, we survey several state-of-the-art histogram-based techniques for compressing databases and data cubes, ranging from one-dimensional to multidimensional data domains. Specifically, we highlight similarity and differences existing among the investigated techniques, and put-in-evidence how proposals have evolved over time towards more and more sophisticated and very-efficient solutions, beyond early experiences focused on selectivity estimation issues within the core layer of DBMS.
background
A database D is a tuple D = (W,I,F) such that (i) W is the schema of D; (ii) I is the instance of D, that is, its realization in terms of collections of tuples adhering to W; (iii) F is the collection of functional dependencies defined over W. In turn, W is a collection of relation schemas W = {T ,
Ti. A functional dependence is expressed as a logical rule over attributes of T . The instance of a relation scheme T is named as relation, and denoted by Ri.
A data cube L is a tuple L = (C,J,H,M), such that: (i) C is the data domain of L containing (OLAP) data cells, which are the basic SQL aggregations of L computed against the relational data source S alimenting L; (ii) J is the set of dimensions of L, that is, the functional attributes (of S) with respect to which the underlying OLAP analysis is defined (in other words, J is the set of attributes with respect to which relational tuples in S are aggregated); (iii) H is the set of hierarchies related to the dimensions of L, that is, hierarchical representations of the functional attributes shaped-in-the-form-of generic trees; (iv) M is the set of measures of L, that is, the attributes of interest (of S) for the underlying OLAP analysis (in other words, M is the set of attributes with respect to which SQL aggregations stored in data cells of L are computed).
Figure 2. A taxonomy of histograms 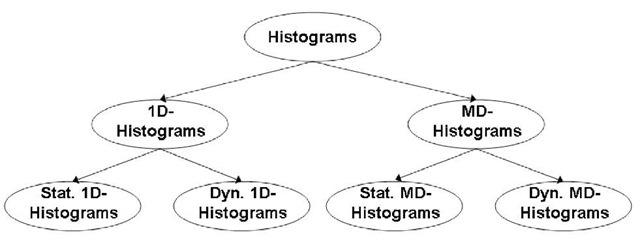
histogram-based compression techniques for databases and data cubes
Classes of Histograms
We distinguish between one-dimensional histograms, those devoted to compress one-dimensional data domains, and multidimensional histograms, those working on multidimensional data domains, which are more interesting than the former, and can be found in a wide range of modern, large-scale, data-intensive applications. Moreover, we can also further distinguish between static histograms and dynamic histograms. The first ones are statically computed against the target domain, and are not particularly suitable to efficiently accomplish data updates occurring on original data sources. The second ones are dynamically computed by taking into consideration, beyond the target domain, or, in some cases, a synopsis of it, other entities related to the dynamics of the target DBMS/OLAP server such as query-workloads, query feedbacks, load balancing issues, and so forth. Contrary to the previous histogram class, dynamic histograms efficiently support update management, being their partition dependent on a “parametric” configuration that can be easily (re-)computed at will. From this classification, a simple-yet-effective taxonomy of histograms can be derived (see Figure 2).
Static One-Dimensional Histograms
One-dimensional histograms deal with the problem of approximating a one-dimensional data domain or, equally, a one-dimensional data distribution. As an example, one-dimensional histograms can be used to approximate the domain/distribution of an attribute R.A of a given relation R of a RDBMS server to selectivity estimation purposes. Such histograms represent first research experiences in this field, and have been proposed in the context of query optimizers mainly (Kooi, 1980).
Let B be the whole number of buckets of the final histogram, obtaining an equal number of rows per bucket is the goal of (one-dimensional) Equi-depth histogram, introduced by Piatetsky-Shapiro and Connell (Piatetsky-Shapiro et al., 1984), that propose a simple construction procedure based on first sorting, and then taking B—1 equally-spaced splits of the target domain. This approach can be improved by first sampling, and then taking equally-spaced splits of the sampled domain instead of the original domain (Piatetsky-Shapiro et al., 1984), or applying one-pass quantile algorithms (Greenwald & Khanna, 2001). Maintaining such histogram is also very efficient as it can be maintained using one-pass algorithms, or a backing sample (Gibbons et al., 1997), which, essentially, consists in keeping bucket counts up-to-date.
Poosala et al. (1996) propose compressing Equi-Depth histograms by creating singleton buckets for largest values, and maintaining the equi-depth strategy over the rest of data. This allows the “original” version of the Equi-Depth histogram to be improved significantly, as exact information is kept for largest values, whereas less-detailed information is maintained for the rest of data. The construction of such compressed histogram can be implemented by (i) sorting buckets, (ii) scanning the buckets looking for the largest values (this is done in time O(B-logB)), and, finally, (iii) performing a one-pass scan in order to process the remaining data. Alternatively, sampling can be used to improve performance, similarly to the “original” version of the histogram. Gibbons et al. (1997) propose maintaining compressed Equi-Depth histograms by using the split-&-merge approach as in the uncompressed ones, but also taking in account the issue of deciding when to create and remove singleton buckets.
In a V-Optimal histogram, introduced by Ioannidis and Poosala (1995), buckets are selected in such a way as to minimize frequency variance within them. In Ioannidis and Poosala (1995), authors show that V-Optimal histogram minimizes the average selectivity estimation error for equality-joins and selections. Following the original idea, V-Optimal construction method has been further improved by Jagadish et al. (1998), that give-to-this-end an O(B-n2) time dynamic programming algorithm, such that (i) B is (still) the overall number of buckets of the histogram, and (ii) n is the number of items of the input data domain D (i.e., the size of D).
Dynamic One-Dimensional Histograms
In the case of dynamic one-dimensional histograms, the final histogram is computed by considering additional information apart from the target data domain (or a synopsis of it). A relevant instance of such class of histograms is represented by the so-called Self-Tuning histogram (ST-histogram), introduced by Aboulanaga and Chaudhuri (1999), that propose improving the original version of Equi-Depth histogram via tuning bucket frequencies by (i) comparing actual selectivity to histogram estimate, (ii) using this information to adjust bucket frequencies by dividing the values of each bucket by a quantity equal to DF-SE, where Dpis the dampening factor, and SE is the actual error, and, finally, (iii) restructuring the histogram by merging buckets of near-equal-frequencies and splitting large-frequency buckets.
Static Multidimensional Histograms
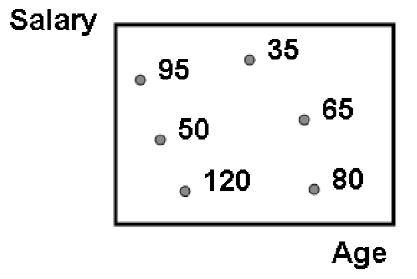
The basic problem addressed by techniques for compressing multidimensional domains is to approximate the joint data distribution of multiple attributes, obtained by jointly combining the distributions of singleton attributes. For instance, in Figure 3 a two-dimensional data domain on salary and age of employers is depicted; in each dimension, a distinctive data distribution related to the singleton attribute can be identified.
Figure 3. A two-dimensional joint data distribution
The goal of these techniques is to provide selectivity estimation for queries with multiple predicates, like in Mu-ralikrishna and DeWitt (1998), and to approximate general relations, like in Poosala and Ioannidis (1997), or OLAP data cubes, like in Vitter et al. (1998). A popular and conventional approach is based on the well-known attribute-value independence (AVI) assumption (Selinger et al., 1979), according to which any query involving a set of attributes can be answered by applying it on each attribute singularly. This approach is theoretically reasonable, but it has been recognized as source of gross errors in practice (e.g., (Christodoulakis, 1984; Faloutsos & Kamel, 1997; Poosala, 1997; Poosala & Ioannidis, 1997). To cope with this problem, multidimensional histograms use a small number of multidimensional buckets to directly approximate the joint data distribution. The approximate d-dimensional distribution f is obtained from the actual d-dimensional distribution fvia (i) setting the total bucket frequency F, and (ii) approximating data points of f on a w(0)x w(1)x… x w{jdj-2)x w(/d/-1) uniform grid G, such that w(k) is the number of distinctive values along the dimension dk, and each cell of G has a bucket frequency equal to F / {w(0)-w(1)-…-w(/d/-2)-w(/d/-1)).
However, even if reasonable, this approach introduces serious limitations when applied to real-life databases and data cubes. Indeed, constructing histograms is much harder for two dimensions than for the one-dimensional case, as recognized by Muthukrishnan et al. (1999). This problem gets worse in the case that the dimension number increases, and becomes a problematic bottleneck in real-life data-intensive systems where corporate databases and data cubes with more than 100 dimensions can be found. From this evidence, various and heterogeneous alternatives to the problem of computing multidimensional histograms have been proposed in literature, each of them based on one or more properties of data distributions characterizing the input data domain. Conventional approaches take into consideration statistical and error-metrics-based properties of data distributions. Other approaches expose greedy solutions, as traditional approaches introduce excessive computational overheads on highly-dimensional data domains.
Among all the alternatives, we focus our attention on the following (static) multidimensional histograms, mainly because they can be considered as representative and significant experiences in this context: Equi-Depth (Muralikrishna & DeWitt, 1998), MHist (Poosala & Ioannidis, 1997), Min-Skew (Acharya et al., 1999), GenHist (Gunopulos et al., 2000), and GHBH (Furfaro et al., 2005) histograms.
Given a d-dimensional data domain D (e.g., a data cube), (multidimensional) Equi-Depth histogram Hed(D), proposed by Muralikrishna and DeWitt (1998), is built as follows: (i) fix an ordering of the d dimensions; (ii) set a « ldlth root of desired number of buckets; (iii) initialize HE d(D) to the input data distribution of D, (iV) for each k in {0, 1, …, |d|-1} split each bucket in HED(D) in a equi-depth partitions along dk; finally, (v) return resulting buckets to HDD). This technique presents some limitations: fixing a and the dimension ordering can result in poor partitions, and, consequently, there could be a limited level of bucketization that, in turn, involves low quality of HED(D) in its general goal of approximating D.
MHist histogram, proposed by Poosala and Ioannidis (1997), overcomes Equi-Depth performance. MHist build procedure depends on the parameter p (specifically, such histogram is denoted by MHist-p): contrarily to the previous technique, at each step, the bucket bi in a MHist histogram Hmh(D) containing the dimension dk whose marginal is the most in need of partitioning is chosen, and it is split along dk into p (e.g., p = 2) buckets. Experimental results shown in Poosala and Ioannidis (1997) state that MHist overcomes AVI and Equi-Depth.
Min-Skew histogram was originally designed by Acharya et al. (1999) to tackle the problem of selectivity estimation of spatial data in geographical information systems (GIS). Spatial data are referred to spatial (or geographical) entities such as points, lines, poly-lines, polygons and surfaces, and are very often treated by means of minimal rectangles containing them, namely Minimum bounding rectangles (MBR). Min-Skew is more sophisticated than MHist. The main idea behind a Min-Skew histogram HMS(D is to follow the criterion of minimizing the spatial skew of the histogram by performing a binary space partitioning (BSP) via recursively dividing the space along one of the dimensions each time. More formally, each point in the space of a given GIS instance is associated to a spatial density, defined as the number of MBR that contain such a point. When performing the partition, each bucket bi is assigned the spatial skew si, defined as follows: s= ^^=0 (fj – f)2 / n„ where (i) n. is the number of points contained within b,, (ii) f is the spatial frequency of the jth point within b, and (iii) f represents the average frequency of all the points within b.. The total skew
Sof H (D is defined as follows: S = 1 n. • s, where (i) B is the total number of buckets, (ii) si is the spatial skew associated with bucket b, and (iii) n. is the number of points of b.. The construction technique of HMS(D) tries, at each step, to minimize the overall spatial skew of the histogram by selecting (i) a bucket to be split, (ii) a dimension of the multidimensional space along which split, and (iii) a splitting point along that dimension such that the overall spatial skew computed after the split is smaller than the one computed at the previous step (i.e., before the current split). Finally, noticing that the spatial skew captures the variance of the spatial density of MBR within each bucket, we can say that Min-Skew follows, in some sense, the spirit of V-Optimal.
Gunopulos et al. propose GenHist histogram (2000), a new kind of multidimensional histogram that is different from the previous ones with respect to the build procedure. The key idea is the following: given an histogram H whit hb buckets on an input data domain D, a GenHist histogram Hgh(D) is built by finding nb overlapping buckets on H, such that nb is an input parameter. To this end, the technique individuates the number of distinct regions that is much larger than the original number of buckets hb, thanks to a greedy algorithm that considers increasingly-coarser grids. At each step, such algorithm selects the set of cells J of highest density, and moves enough randomly-selected points from Jinto a bucket to make Jand its neighbors “close-to-uniform.” Therefore, the novelty of the proposal consists in defining a truly multidimensional splitting policy, based on the concept of tuple density. A drawback of the GenHist proposal is the difficulty of choosing the right values for setting the input parameters, which are: (i) the degree of the grid used to obtain regular partitions of the data domain at each iteration; (ii) the number of buckets b created at each iteration; (iii) the value a, which controls the rate by which decreases. Indeed, authors state that: (i) the optimal setting for the initial value of denoted by must be such that, at the first iteration, the percentage of points that are removed from the input data cube to provide b buckets is at least
(ii) the optimal setting for a is a = (1/2)1/d, such that dis the number of dimensions of the input data cube.
More recently, Furfaro et al. (2005) propose a new kind of multidimensional histogram which can be considered as very innovative if compared with previous ones. They first propose the definition of a new class of histograms, called flat binary histogram (FBH), which are characterized by the property that buckets are represented independently from one another, without exploiting the hierarchical structure of the underlying partition. Then, they classify MHist and Min-Skew inside the class FBH histograms, and give theoretical motivations to this claim. Finally, they introduce the grid hierarchical binary histogram (GHBH), a new histogram belonging to the FBH class. The partition scheme used by a GHBH histogram HGHBH(D is the same of that of MHist and Min-Skew histograms, thus based on (i) statistical properties of data, like the standard deviation, and (ii) greedy (generating) algorithms. The novelty of HGHBH(D) is that the hierarchy adopted to determine the structure of the histogram is also used to represent it, thus introducing surprising efficiency in terms of both space consumption and accuracy of query estimations. Furthermore, HGHBH(D is based on a constrained partition scheme, where buckets of data cannot be split anywhere along one of their dimensions, but the split must be laid onto a grid partitioning the bucket into a number of equally-sized sub-buckets. The adoption of this constrained partitioning enables a more efficient physical representation of the histogram with respect to other histograms using more traditional partition schemes. Thus, the saved space can be invested to obtain finer grain buckets, which approximate data in more detail. Indeed, the ability of creating a larger amount of buckets (in a given storage space) does not guarantee a better accuracy in estimating range-queries, as it could be the case that buckets created by adopting a constrained scheme contain very skewed (i.e., non-uniform) distributions. In Furfaro et al. (2005), authors show that given a d-dimensional data domain D and the space bound M(i.e., the storage space available for housing the output compressed data structure), the maximum number of buckets p™ within M of a FBH over D, denoted by HFBH(D), is
assuming that an integer value is represented using 32 bits. On the contrary, using Hghbh(D), the maximum number of buckets PmaxBH within Mis
such that 8 is the “degree” of the grid-based constrained partition scheme.
Dynamic Multidimensional Histograms
Dynamic multidimensional histograms extend capabilities of static multidimensional histograms by incorporating inside their generating algorithms the amenity of building/refining the underlying partition in dependence on non-conventional entities related to the dynamic behavior of the target DBMS/ OLAP server, such as query-workloads. Among this class of histograms, relevant proposal are: wavelet-based (Matias et al., 1998) and STHoles (Bruno et al., 2001) histograms, and our innovative data structure TP-Tree (Cuzzocrea & Wang, 2007).
Wavelet-based histograms, proposed by Matias et al. (1998), aim at combining the benefits coming from the usage of wavelet transformations in the context of data-compression/approximate-query-answering (Vitter et al., 1998) (basically, these benefits can be synthesized in a greater flexibility in supporting different classes of queries rather than histograms) with histograms. The key idea of this approach is to use a compact subset of Haar (or linear) wavelet coefficients to approximate the data distribution.
This approach has provided good results in range-query selectivity estimation issues, and has outperformed performance of original histograms. Subsequently, authors have then addressed the problem of the dynamic maintenance of wavelet-based histograms (Matias et al., 2000). Here, they observe that updates in singleton distribution value can affect the values of many coefficients through propagations like paths-to-the-root of the decomposition tree given by the wavelet transformation; therefore, they develop a dynamic technique in which as distribution changes, “most significant” (e.g., largest) wavelet coefficients are updated consequentially.
Bruno et al. (2001) propose a different kind of multidimensional histogram, based on the analysis of the query-workload on it: the workload-aware histogram, which they call STHoles. Rather than an arbitrary overlap, a STHoles histogram HST(D) allows bucket nesting, thus achieving the definition of the so-called bucket tree. Query-workloads are handled as follows: the query result stream QRto be analyzed is intercepted and, for each query Q. belonging to QR and for each bucket b. belonging to the current bucket tree, the number |Q.. 0 bj is counted. Then, “holes” in b. for regions of different tuple density are “drilled” and “pulled out” as children of b Finally, buckets of similar densities are merged in such a way as to keep the number of buckets constant. Hst(D) makes use of a tree-like in-memory-data-structure, since the parent-child relationship in a tree is comparable to the nest relationship, and the sibling-sibling relationship is represented by buckets nested within the same external bucket, (nested buckets look-like holes within external buckets—the name STHoles comes from this). The construction algorithm of HST(D) does not take into account the original data set; indeed, the needed information is instead gathered by inspecting the target query-workload and query feedbacks. This amenity makes HST(D) self tunable, that is, adaptable to updates and modifications in the original data cube. On the basis of this approach, a relevant amount of the total storage space available for housing the histogram is invested in representing “heavy-queried regions,” thus providing a better approximation for such regions, whereas a fewer storage space is reserved to “lowly-queried regions,” admitting some inaccuracy (however, tolerable in OLAP context (Cuzzocrea, 2005a)) for such regions. More specifically, Hst(D) construction algorithm is outlined in the following. Given an input data cube L and a query-workload QWL={Qff Qi>->Q\qwl\J, for each query Q. e QWL at iterationj, new buckets are generated by intersecting each bucket bi of the current partition P.(L) with Q, thus determining the set of candidate buckets U = {bc | . = Q. 0 b,, b . e P.(L), Q. e QWL, Q . Ob. 4 0}; if such buckets have densities notably different from their parents’ ones, then these new buckets are definitively added to the current partition. This process is iterated until the histogram reaches the maximum number of allowed buckets (i.e., the whole available storage space is consumed). At this point, in order not to exceed the given amount of storage space, after candidate buckets are added to the current partition, the algorithm finds couples of buckets linked together by either a parent-child relationship or a sibling-sibling relationship, and having the closest densities. The size reduction is accomplished by performing either a parent-child or a sibling-sibling merge between the components of these couples, until the histogram fits within the given amount of storage space. A thorough set of experimental results on both real-life and synthetic data sets demonstrates that STHoles overcomes performance of Equi-Depth,MHist, and GenHist; in addition to this, (Bruno et al., 2001) authors also show that, on the DBMS Microsoft SQL Server, query-workload analysis overheads introduced by STHoles are very low, less than 10 percent of the overall DBMS throughput.
Tunable-partition-tree (TP-Tree), proposed by Cuz-zocrea & Wang (2007), is a tree-like, highly-dynamic data structure that codifies a multidimensional histogram for massive (multidimensional) data cubes, denoted by HTp(D), whose partition varies over time according to the query-workload against the target OLAP server. For this reason, partitions of HTp(D are named as tunable partitions, and HTp(D is said to be a “workload-aware” synopsis data structure. This approach resembles that proposed by Bruno et al. (2001). The main contribution of the TP-Tree proposal with respect to previous techniques consists in introducing models and algorithms having low computational costs, whereas previous techniques are, usually, time-consuming and resource-intensive. Data stored inside buckets of TP- Tree partitions are obtained by (i) sampling the input data cube (from this solution, low computational costs required by the TP-Tree approach follow), and (ii) separately representing, storing, and indexing outliers via high performance quadtree based (data) structures. Outlier management is another innovative and relevant contribution of the TP- Tree proposal, as it allows us to provide probabilistic guarantees over the degree of approximation of the answers, which is a leading research topic very often neglected by the research community (for instance, see (Cuzzocrea, 2005b)). Finally, the TP-Tree data organization is characterized by a hierarchical and multi-resolution nature, which allows us to efficiently answer relevant-in-practice classes of OLAP queries, like range-queries.
future trends
For what regards the basic problem of computing histograms, in order to achieve more and more sophisticated representations beyond actual capabilities of state-of-the-art techniques, next years’ challenges for histogram research are the following. (i) Error guarantees. No one of the surveyed state-of-the-art techniques consider the relevant issue of building histograms capable of ensuring a fixed threshold over the (query) error due to the approximate evaluation of queries against such data structures. Indeed, the next frontier of histogram research is represented by the challenge of ensuring error guarantees over the final data structures; some initiatives devoted to fill the actual gap in this context are (Cuzzocrea & Wang, 2007; Koudas et al., 2000), whereas similar efforts in wavelet-based database and data cube approximation, which is a research issue close to ours, are Garofalakis and Gibbons (2002); Garofalakis and Kumar (2004). (ii) Flexibility for wide families of queries. One of the most important limitations of histograms is the fact that they are “build-one-use-many-times” data structures, meaning that state-of-the-art techniques construct histograms for a specific family of queries, for example, those given by typical query-workloads of the target DBMS/OLAP server, so that it could happen to obtain high accuracy on certain queries, and, contrarily, low accuracy on different queries. This is a problematic issue to be handled, and can be reasonable considered as a leading open problem for histogram research.
Also in-consequence-of influencing insights given by Ioannidis (2003), for what regards the integration of histogram-based techniques with other popular data-intensive techniques, main future directions can be summarized by the following points. (i) Integration of histogram-based and clustering techniques. Computing clusters of a given item set defines the same problem of computing a histogram as a collection of buckets over that item set, given that (i) clustering is, similarly to histogram-based ones, a partition-based technique, and (ii) buckets are conceptually the same of clusters, since in clustering we want to generate clusters such that intra-cluster distance is small and extra-bucket distance is big, and, symmetrically, in buckets we aggregate data having, for instance, low variance (which, in turn, is a distance-based metrics), whereas among buckets we want to obtain big variance. In literature, there exists a wide number of clustering techniques, so that it is very interesting to study how these proposals can be applied to the problem of computing histograms, and, specifically, multidimensional histograms, given that research communities have devoted a great deal of attention to the problem of clustering high-dimensional domains. (ii) Integration of histogram-based and pattern recognition techniques. Choosing the parameters according to which computing buckets (e.g., variance, skewness, etc.) is similar to the problem of establishing which parameters are similar for items of a given item set in order to group items according to these parameters. The simplest case of such kind of problems is to choose a dimension among all the dimensions of a given domain to grouping/clustering purposes. Specifically, this general problem is recognized in literature as the pattern recognition problem. Just like the histograms/clustering symmetry, it is also very interesting to study how pattern recognition techniques can influence histogram research. (iii) Integration of histogram-based and tree-like indexing techniques. A hierarchical indexing data structure is very similar to a hierarchical histogram, where each level is partitioned according to a criterion that is inspired to classical histogram-based techniques. This similarity leads to, from a side, (i) the definition of high-performance indexing data structures for massive data sets that exploit consolidate results of histogram research, and, from the other side, (ii) the idea of adopting successful methodologies of RDBMS indexes (e.g., B+-trees, R-trees, etc.) to the problem of computing histograms for one-dimensional and multidimensional domains.
conclusion
Due to an impressive proliferating of data-intensive systems in real-life applications, the problem of compressing massive databases and data cubes play a critical role in database and data warehouse research. On the other hand, this problem has significantly stimulated research communities during the last two decades, and, presently, it continues attracting attention and efforts of research communities, also thanks to innovative, previously-unrecognized knowledge production, processing, and fruition paradigms drawn by emerging technologies like those of data stream management systems and sensor network data management systems. In consequence of this, a plethora of database and data cube compression techniques have been proposed in literature, with different aims and goals (and fortune). Among these, histogram-based techniques are a very popular solution of tackling research challenges posed by compressing massive databases and data cubes, and have been extensively studied and investigated since early 1980 and before. The result we observe at now is a wide literature on histogram-based techniques, which, in our opinion, will continue to stimulate research communities towards investigating new and exciting problems that, basically, concern the core layer of DBMS and OLAP servers, with also important influences on commercial platforms. Given these considerations, in this article we surveyed state-of-the-art histogram-based techniques for compressing databases and data cubes, ranging from one-dimensional to multidimensional data domains. As an additional contribution, a simple-yet-effective taxonomy of histograms has been provided.
key terms
Multidimensional OLAP (MOLAP): An in-memory-storage model that represents a multi-dimensional data cube in form of a multi-dimensional array.
OLAP Query: A query defined against a data cube that introduces a multidimensional range (via specifying an interval for each dimension of the data cube) and a SQL aggregate operator, and returns as output the aggregate value computed over cells of the data cube contained in that range.
Online Transaction Processing (OLTP): A methodology for representing, managing and querying DB data generated by user/application transactions according to flat (e.g., relational) schemes.
Online Analytical Processing (OLAP): A methodology for representing, managing and querying massive DW data according to multidimensional and multi-resolution abstractions of them.
Relational Query: A query defined against a database that introduces some predicates (e.g., Boolean) over tuples stored in the database, and returns as output the collection of tuples satisfying those predicates.
Selectivity of an OLAP Query: A property of an OLAP query that estimates the cost required to evaluate that query. It is usually model in terms of the geometrical volume of the query range.
Selectivity of a Relational Query: A property of a relational query that estimates the cost required to evaluate that query. It is usually model in terms of the number of tuples involved by the query.