1.3
Selection of an induction motor and its control scheme depends on the load. An ASD of a fan will certainly differ from that of a winder in a paper mill, the manufacturing process in the latter case imposing narrow tolerance bands on speed and torque of the motor. Various classifications can be used with respect to loads. In particular, they can be classified with respect to: (a) inertia, (b) torque versus speed characteristic, and (c) control requirements.
High-inertia loads, such as electric vehicles, winders, or centrifuges, are more difficult to accelerate and decelerate than, for instance, a pump or a grinder. The total mass moment of inertia referred to the motor shaft can be computed from the kinetic energy of the drive. Consider, for example, a motor with the rotor inertia of Ju that drives a load with the mass moment of inertia of Jh through a transmission with the gear ratio of N. The kinetic energy, EL, of the load rotating with the angular velocity
![tmp2B7-1_thumb[3] tmp2B7-1_thumb[3]](http://lh5.ggpht.com/_X6JnoL0U4BY/S1hVfk6efRI/AAAAAAAAH4M/FZ5RupyeYuw/tmp2B71_thumb3_thumb.png?imgmax=800)
![tmp2B7-2_thumb[1] tmp2B7-2_thumb[1]](http://lh3.ggpht.com/_X6JnoL0U4BY/S1hVg7XntTI/AAAAAAAAH4U/Z2O8WOeRgDE/tmp2B72_thumb1_thumb.png?imgmax=800)
while the kinetic energy, EM, of the rotor whose velocity is o>M is given by
![tmp2B7-3_thumb[1] tmp2B7-3_thumb[1]](http://lh5.ggpht.com/_X6JnoL0U4BY/S1hViNbYGmI/AAAAAAAAH4c/aiWZbjAT8Ms/tmp2B73_thumb1_thumb.png?imgmax=800)
Thus, the total kinetic energy, ET, of the drive can be expressed as
![tmp2B7-4_thumb[1] tmp2B7-4_thumb[1]](http://lh6.ggpht.com/_X6JnoL0U4BY/S1hVjn5TcqI/AAAAAAAAH4k/3bg0Fjh9Cxw/tmp2B74_thumb1_thumb.png?imgmax=800)
where JT denotes the total mass moment of inertia of the system referred to the motor shaft. Because
![tmp2B7-5_thumb[1] tmp2B7-5_thumb[1]](http://lh6.ggpht.com/_X6JnoL0U4BY/S1hVk4cOlLI/AAAAAAAAH4s/w1RUMoHXixY/tmp2B75_thumb1_thumb.png?imgmax=800)
then
![tmp2B7-6_thumb[1] tmp2B7-6_thumb[1]](http://lh4.ggpht.com/_X6JnoL0U4BY/S1hVmPrbpsI/AAAAAAAAH40/gqfZF3RIU5w/tmp2B76_thumb1_thumb.png?imgmax=800)
The difference, Td, between the torque, TM, developed in the motor and the static torque, Th, with which the load resists the motion is called a dynamic torque. According to Newton’s second law,
![tmp2B7-7_thumb[1] tmp2B7-7_thumb[1]](http://lh3.ggpht.com/_X6JnoL0U4BY/S1hVnellMbI/AAAAAAAAH48/HMLJQkJiYyQ/tmp2B77_thumb1_thumb.png?imgmax=800)
or
![tmp2B7-8_thumb[1] tmp2B7-8_thumb[1]](http://lh3.ggpht.com/_X6JnoL0U4BY/S1hVotqQLKI/AAAAAAAAH5E/SjR6wF037ok/tmp2B78_thumb1_thumb.png?imgmax=800)
Unsurprisingly, the preceding equation indicates that a high mass moment of inertia makes a drive sluggish, so that a high dynamic torque is required for fast acceleration or deceleration of the load.
The concept of an equivalent wheel is convenient for calculation of the total mass moment of inertia referred to the shaft of a motor driving an electric vehicle or another linear-motion load. The equivalent wheel is a hypothetical wheel assumed to be directly driven by the motor and whose peripheral velocity, ml, equals the linear speed of the load. Denoting the radius of the equivalent wheel by req, the speed of the load can be expressed in terms of that radius and motor speed as
![tmp2B7-9_thumb[1] tmp2B7-9_thumb[1]](http://lh5.ggpht.com/_X6JnoL0U4BY/S1hVpif2xgI/AAAAAAAAH5M/LliHNUslA9k/tmp2B79_thumb1_thumb.png?imgmax=800)
The equation for kinetic energy, Eh, of the load whose mass is denoted by mL,
![tmp2B7-10_thumb[1] tmp2B7-10_thumb[1]](http://lh5.ggpht.com/_X6JnoL0U4BY/S1hVqzipzGI/AAAAAAAAH5U/OHLVrKoz33g/tmp2B710_thumb1_thumb.png?imgmax=800)
can therefore be rearranged to
![tmp2B7-11_thumb[1] tmp2B7-11_thumb[1]](http://lh4.ggpht.com/_X6JnoL0U4BY/S1hVsAHjvDI/AAAAAAAAH5c/FFFEQUZ7tl0/tmp2B711_thumb1_thumb.png?imgmax=800)
with 7L denoting the effective mass moment of inertia of the load, given by
![tmp2B7-12_thumb[1] tmp2B7-12_thumb[1]](http://lh6.ggpht.com/_X6JnoL0U4BY/S1hVtRaI_nI/AAAAAAAAH5k/_AKnAe6GSAg/tmp2B712_thumb1_thumb.png?imgmax=800)
Because the motor is assumed to drive the equivalent wheel directly (i.e., N = 1), the total mass moment of inertia, /x, is equal to the sum of JL and JM.
In most loads, the static torque, TL, depends on the load speed, coL. The rL(a)L) relation, usually called a mechanical characteristic, is an important feature of the load, because its intersection with the analogous characteristic of the motor, 7M(o)M), determines the steady-state operating point of the drive. Expressing the mechanical characteristic by a general equation
![tmp2B7-13_thumb[1] tmp2B7-13_thumb[1]](http://lh5.ggpht.com/_X6JnoL0U4BY/S1hVulsOkFI/AAAAAAAAH5s/R2v_Qu7N19U/tmp2B713_thumb1_thumb.png?imgmax=800)
where Tw and t are constants, three basic types, illustrated in Figure 1.1, can be distinguished:

FIGURE I. I Mechanical characteristics of common loads.
1. Constant-torque characteristic, with k *=» 0, typical for lifts and conveyors and, generally, for loads whose speed varies in a narrow range only.
2. Progressive-torque characteristic, with k > 0, typical for pumps, fans, blowers, compressors, electric vehicles and, generally, for most loads with a widely varying speed.
3. Regressive-torque characteristic, with k < 0, typical for winders. There, with a constant tension and linear speed of the wound tape, an increase in the coil radius is accompanied by a decreasing speed and an increasing torque.
Practical loads are better described by operating areas rather than mechanical characteristics. An operating area represents a set of all allowable operating points in the (coL,rL) plane. Taking a pump as an example, its torque versus speed characteristic strongly depends on the pressure and viscosity of the pumped fluid. Analogously, the mechanical characteristic of a winder varies with changes in the tape tension and speed. Therefore, a single mechanical characteristic cannot account for all possible operating points. An example operating area of a progressive-torque load is shown in Figure 1.2a. Clearly, if a load is driven directly by a motor, the motor operating area in the (coM,rM) plane is the same as that of the load. However, if the load is geared to the motor, the operating areas of the load and motor differ because the gearing acts as a transformer of the mechanical power. The operating area of a motor driving the load in Figure 1.2a through a frictionless transmission with a gear ratio of 0.5 is shown in Figure 1.2b.
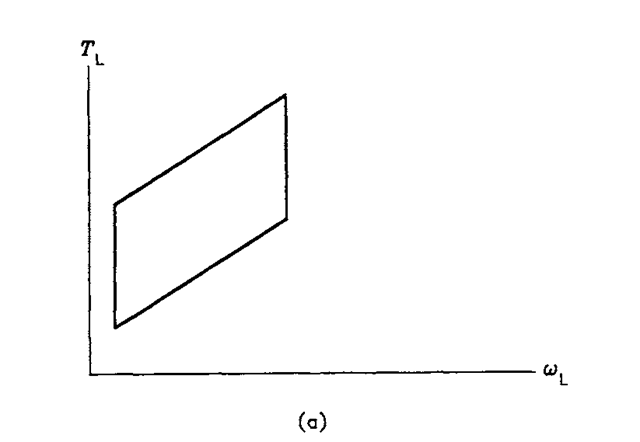
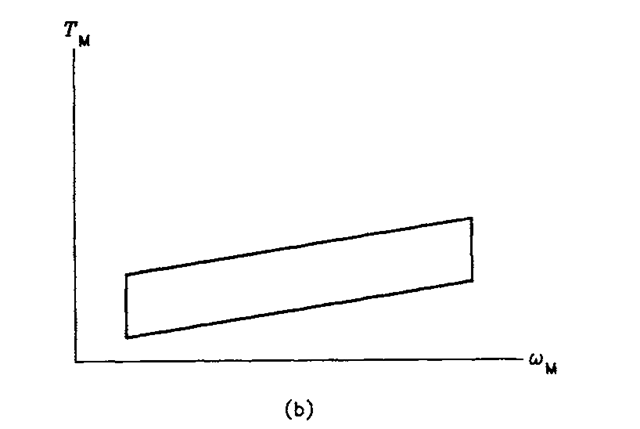
FIGURE 1.2 Example operating areas: (a) load, (b) motor (same speed and torque scales used in both diagrams).
In a properly designed drive system, the motor operates safely at every point of its operating area, that is, neither the voltage, current, nor speed exceeds its allowable values. The gearing may be needed to provide proper matching of the motor to the load. A gear ratio less than unity is employed when the load is to run slower than the motor, with a torque greater than that of the motor. Conversely, a high-speed, low-torque load requires a gear ratio greater than unity.
Control requirements depend on the particular application of a drive system. In most practical drives, such as those of pumps, fans, blowers, conveyors, or centrifuges, the main controlled variable is the load speed. High control accuracy in such systems is usually not necessary. Drives with a directly controlled torque, for instance those of winders or electric vehicles, are more demanding with regard to the control quality. Finally, positioning systems, such as precision machine tools or elevator drives, must be endowed with the highest level of dynamic performance. In certain positioning systems, control requirements are so strict that induction motors cannot be employed.
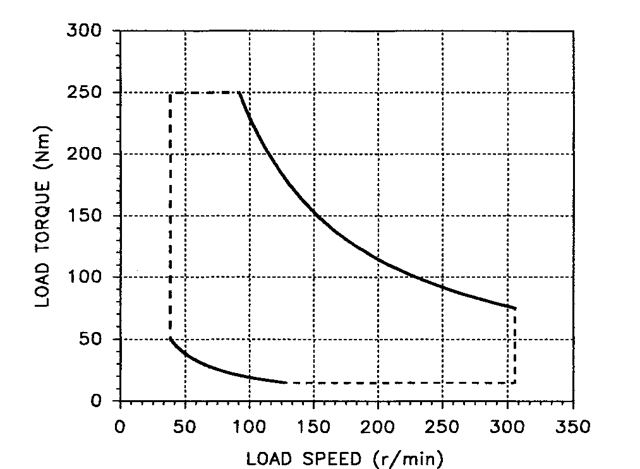
FIGURE 1.3 Operating area of the example winder.
COMMON LOADS (Induction Motor)
Next post: OPERATING QUADRANTS (Induction Motor)
Previous post: DRIVE SYSTEMS WITH INDUCTION MOTORS
