Positioning, or finding the user’s location, with GPS requires some understanding of the GPS signal structure and how the measurements can be made. Likewise, as the GPS signal is received through a GPS receiver, understanding the capabilities and limitations of the various types of GPS receivers is essential. Furthermore, the GPS measurements, like all measurable quantities, contain errors and biases, which can be removed or reduced by combining the various GPS observables. This topic discusses these issues in detail.
GPS signal structure
The two carrier frequencies are generated at 1,575.42 MHz (referred to as the L1 carrier) and 1,227.60 MHz (referred to as the L2 carrier). The corresponding carrier wavelengths are approximately 19 cm and 24.4 cm, respectively, which result from the relation between the carrier frequency and the speed of light in space [1, 2]. The availability of the two carrier frequencies allows for correcting a major GPS error, known as the ionospheric delay.All of the GPS satellites transmit the same L1 and L2 carrier frequencies. The code modulation, however, is different for each satellite, which significantly minimizes the signal interference.
The two GPS codes are called coarse acquisition (or C/A-code) and precision (or P-code). Each code consists of a stream of binary digits, zeros and ones, known as bits or chips. The codes are commonly known as PRN codes because they look like random signals (i.e., they are noise-like signals). But in reality, the codes are generated using a mathematical algorithm. Presently, the C/A-code is modulated onto the L1 carrier only, while the P-code is modulated onto both the L1 and the L2 carriers. This modulation is called biphase modulation, because the carrier phase is shifted by 180° when the code value changes from zero to one or from one to zero [3].
The C/A-code is a stream of 1,023 binary digits (i.e., 1,023 zeros and ones) that repeats itself every millisecond. This means that the chipping rate of the C/A-code is 1.023 Mbps. In other words, the duration of one bit is approximately 1 ms, or equivalently 300m [4]. Each satellite is assigned a unique C/A-code, which enables the GPS receivers to identify which satellite is transmitting a particular code. The C/A-code range measurement is relatively less precise compared with that of the P-code. It is, however, less complex and is available to all users.
The P-code is a very long sequence of binary digits that repeats itself after 266 days [1]. It is also 10 times faster than the C/A-code (i.e., its rate is 10.23 Mbps). Multiplying the time it takes the P-code to repeat itself, 266 days, by its rate, 10.23 Mbps, tells us that the P-code is a stream of about 2.35 X 1014 chips! The 266-day-long code is divided into 38 segments; each is 1 week long. Of these, 32 segments are assigned to the various GPS satellites. That is, each satellite transmits a unique 1-week segment of the P-code, which is initialized every Saturday/Sunday midnight crossing. The remaining six segments are reserved for other uses. It is worth mentioning that a GPS satellite is usually identified by its unique 1-week segment of the P-code. For example, a GPS satellite with an ID of PRN 20 refers to a GPS satellite that is assigned the twentieth-week segment of the PRN P-code. The P-code is designed primarily for military purposes. It was available to all users until January 31,1994 [1]. At that time, the P-code was encrypted by adding to it an unknown W-code. The resulting encrypted code is called the Y-code, which has the same chipping rate as the P-code. This encryption is known as the antispoofing (AS).
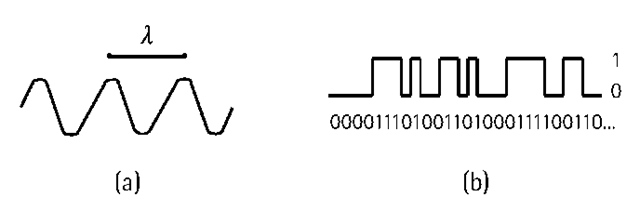
Figure 2.1 (a) A sinusoidal wave; and (b) a digital code.
The GPS navigation message is a data stream added to both the L1 and the L2 carriers as binary biphase modulation at a low rate of 50 kbps. It consists of 25 frames of 1,500 bits each, or 37,500 bits in total. This means that the transmission of the complete navigation message takes 750 seconds, or 12.5 minutes. The navigation message contains, along with other information, the coordinates of the GPS satellites as a function of time, the satellite health status, the satellite clock correction, the satellite almanac, and atmospheric data. Each satellite transmits its own navigation message with information on the other satellites, such as the approximate location and health status [1].
GPS modernization
The current GPS signal structure was designed in the early 1970s, some 30 years ago [5]. In the next 30 years, GPS constellation is expected to have a combination of Block IIR satellites, currently being launched, and Block IIF and possibly Block III satellites. To meet the future requirements, the GPS decision makers have studied several options to adequately modify the signal structure and system architecture of the future GPS constellation. The modernization program aims, among other things, to provide signal redundancy and improve positioning accuracy, signal availability, and system integrity.
The modernization program will include the addition of a civil code (C/A-code) on the L2 frequency and two new military codes (M-codes) on both the L1 and the L2 frequencies [5]. These codes will be added to the last 12 Block IIR satellites, which will be launched at the beginning of 2003. The availability of two civil codes (i.e., C/A-code on both L1 and L2 frequencies) allows a user with a stand-alone GPS receiver to correct for the effect of the ionosphere (the upper layer of the atmosphere), which is a major error source.With the termination of selective availability, it is expected that once a sufficient number of satellites with the new capabilities is available, the autonomous GPS horizontal accuracy will be about 8.5m (95% of the time) or better [5].
The addition of the C/A-code to L2, although it improves the autonomous GPS accuracy, was found to be insufficient for use in the civil aviation safety-of-life applications. This is mainly because of the potential interference from the ground radars that operate near the GPS L2 band. As such, to satisfy aviation user requirements, a third civil signal at 1,176.45 MHz (called L5) will be added to the first 12 Block IIF satellites along with the C/A-code on L2 and the M-code on L1 and L2, as part of the modernization program [5]. This third frequency will be robust and will have a higher power level. In addition, this new L5 signal will have wide broadcast bandwidth (a minimum of 20 MHz) and a higher chipping rate (10.23 MHz), which provide higher accuracy under noisy and multipath conditions. The new code will be longer than the current C/A-code, which reduces the system self-interference through the improvement of the auto-and cross-correlation properties. Finally, the broadcast navigation message of the new signal, although containing more or less the same data as the L1 and L2 channels, will have an entirely different, more efficient, structure. The first Block IIF satellite is scheduled to be launched in 2005 or shortly after that date. The addition of these capabilities will dramatically improve the autonomous GPS positioning accuracy. As well, the real-time kinematic (RTK) users, who require centimeter-level accuracy in real time, will be able to resolve the initial integer ambiguity parameters instantaneously.
The modernization of GPS will also include the studies for the next generation Block III satellites, which will carry GPS into 2030. Finally, the GPS ground control facilities will also be upgraded as a part of the GPS modernization program. With this upgrade, the expected standalone GPS horizontal accuracy will be 6m (95% of the time) or better [5].
Types of GPS receivers
In 1980, only one commercial GPS receiver was available on the market, at a price of several hundred thousand U.S. dollars [6]. This, however, has changed considerably as more than 500 different GPS receivers are available in today’s market (see, for example, the January 2001 issue of GPS World magazine). The current receiver price varies from about $100 for the simple handheld units to about $15,000 for the sophisticated geodetic quality units. The price will continue to decline in the future as the receiver technology becomes more advanced. A GPS receiver requires an antenna attached to it, either internally or externally. The antenna receives the incoming satellite signal and then converts its energy into an electric current, which can be handled by the GPS receiver [6, 7].
Commercial GPS receivers may be divided into four types, according to their receiving capabilities. These are: single-frequency code receivers, single-frequency carrier-smoothed code receivers, single-frequency code and carrier receivers, and dual-frequency receivers. Single-frequency receivers access the L1 frequency only, while dual-frequency receivers access both the L1 and the L2 frequencies. Figure 2.2 shows examples of various types of GPS receivers. GPS receivers can also be categorized according to their number of tracking channels, which varies from 1 to 12 channels. A good GPS receiver would be multichannel, with each channel dedicated to continuously tracking a particular satellite. Presently, most GPS receivers have 9 to 12 independent (or parallel) channels. Features such as cost, ease of use, power consumption, size and weight, internal and/or external data-storage capabilities, interfacing capabilities, and mul-tipath mitigation (i.e., type of correlator) are to be considered when selecting a GPS receiver.
The first receiver type, the single-frequency code receiver, measures the pseudoranges with the C/A-code only. No other measurements are available. It is the least expensive and the least accurate receiver type, and is mostly used for recreation purposes. The second receiver type, the single-frequency carrier-smoothed code receiver, also measures the pseudoranges with the C/A-code only. However, with this receiver type, the higher-resolution carrier frequency is used internally to improve the resolution of the code pseudorange, which results in high-precision pseudorange measurements. Single-frequency code and carrier receivers output the raw C/A-code pseudoranges, the L1 carrier-phase measurements, and the navigation message. In addition, this receiver type is capable of performing the functions of the other receiver types discussed above.
Dual-frequency receivers are the most sophisticated and most expensive receiver type. Before the activation of AS, dual-frequency receivers were capable of outputting all of the GPS signal components (i.e., L1 and L2 carriers, C/A-code, P-code on both L1 and L2, and the navigation message).
Figure 2.2 Examples of GPS receivers.
However, after the AS activation, the P-code was encrypted to Y-code. This means that the receiver cannot output either the P-code or the L2 carrier using the traditional signal-recovering technique. To overcome this problem, GPS receiver manufacturers invented a number of techniques that do not require information of the Y-code. At the present time, most receivers use two techniques known as the Z-tracking and the cross-correlation techniques. Both techniques recover the full L2 carrier, but at a degraded signal strength. The amount of signal strength degradation is higher in the cross-correlation techniques compared with the Z-tracking technique.
Time systems
Time plays a very important role in positioning with GPS.In addition, measuring the ranges (distances) from the receiver to the satellites is based on both the receiver and the satellite clocks. GPS is also a timing system, that is, it can be used for time synchronization.
A number of time systems are used worldwide for various purposes [1]. Of these, the Coordinated Universal Time (UTC) and the GPS Time are the most important to GPS users. UTC is an atomic time scale based on the International Atomic Time (TAI). TAI is a uniform time scale, which is computed based on independent time scales generated by atomic clocks located at various timing laboratories throughout the world. In surveying and navigation, however, a time system with relation to the rotation of the Earth, not the atomic time, is desired. This is achieved by occasionally adjusting the UTC time scale by 1-second increments, known as leap seconds, to keep it within 0.9 second of another time scale called the Universal Time 1 (UT1) [8, 9], where UT1 is a universal time that gives a measure of the rotation of the Earth. Leap seconds are introduced occasionally, on either June 30 or December 31. As of July 2001, the last leap second was introduced on January 1, 1999, which made the difference between TAI and UTC time scales to be exactly 32 seconds (TAI is ahead of UTC). Information about the leap seconds can be found at the U.S. Naval Observatory Web site, http://maia.usno.navy.mil.
GPS Time is the time scale used for referencing, or time tagging, the GPS signals. It is computed based on the time scales generated by the atomic clocks at the monitor stations and onboard GPS satellites. There are no leap seconds introduced into GPS Time, which means that GPS Time is a continuous time scale. GPS Time scale was set equal to that of the UTC on January 6, 1980 [8]. However, due to the leap seconds introduced into the UTC time scale, GPS Time moved ahead of the UTC by 13 seconds on January 1, 1999. The difference between GPS and UTC time scales is given in the GPS navigation message.
Pseudorange measurements
The pseudorange is a measure of the range, or distance, between the GPS receiver and the GPS satellite (more precisely, it is the distance between the GPS receiver’s antenna and the GPS satellite’s antenna). As stated before, the ranges from the receiver to the satellites are needed for the position computation. Either the P-code or the C/A-code can be used for measuring the pseudorange.
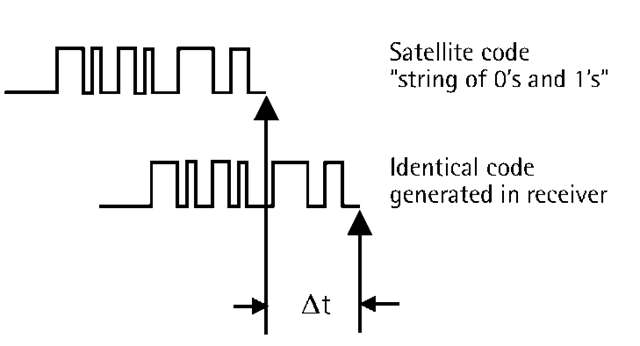
The procedure of the GPS range determination, or pseudoranging, can be described as follows. Let us assume for a moment that both the satellite and the receiver clocks, which control the signal generation, are perfectly synchronized with each other. When the PRN code is transmitted from the satellite, the receiver generates an exact replica of that code [3]. After some time, equivalent to the signal travel time in space, the transmitted code will be picked up by the receiver. By comparing the transmitted code and its replica, the receiver can compute the signal travel time. Multiplying the travel time by the speed of light (299,729,458 m/s) gives the range between the satellite and the receiver. Figure 2.3 explains the pseudorange measurements.
Unfortunately, the assumption that the receiver and satellite clocks are synchronized is not exactly true. In fact, the measured range is contaminated, along with other errors and biases, by the synchronization error between the satellite and receiver clocks. For this reason, this quantity is referred to as the pseudorange, not the range [4].
GPS was designed so that the range determined by the civilian C/A-code would be less precise than that of military P-code. This is based on the fact that the resolution of the C/A-code, 300m, is 10 times lower than the P-code. Surprisingly, due to the improvements in the receiver technology, the obtained accuracy was almost the same from both codes [4].
Figure 2.3 Pseudorange measurements.
Carrier-phase measurements
Another way of measuring the ranges to the satellites can be obtained through the carrier phases. The range would simply be the sum of the total number of full carrier cycles plus fractional cycles at the receiver and the satellite, multiplied by the carrier wavelength (see Figure 2.4). The ranges determined with the carriers are far more accurate than those obtained with the codes (i.e., the pseudoranges) [4]. This is due to the fact that the wavelength (or resolution) of the carrier phase, 19 cm in the case of L1 frequency, is much smaller than those of the codes.
There is, however, one problem. The carriers are just pure sinusoidal waves, which means that all cycles look the same. Therefore, a GPS receiver has no means to differentiate one cycle from another [4]. In other words, the receiver, when it is switched on, cannot determine the total number of the complete cycles between the satellite and the receiver. It can only measure a fraction of a cycle very accurately (less than 2 mm), while the initial number of complete cycles remains unknown, or ambiguous.
Figure 2.4 Carrier-phase measurements.
This is, therefore, commonly known as the initial cycle ambiguity, or the ambiguity bias. Fortunately, the receiver has the capability to keep track of the phase changes after being switched on. This means that the initial cycle ambiguity remains unchanged over time, as long as no signal loss (or cycle slips) occurs [3].
It is clear that if the initial cycle ambiguity parameters are resolved, accurate range measurements can be obtained, which lead to accurate position determination. This high accuracy positioning can be achieved through the so-called relative positioning techniques, either in real time or in the postprocessing mode. Unfortunately, this requires two GPS receivers simultaneously tracking the same satellites in view.
Cycle slips
A cycle slip is defined as a discontinuity or a jump in the GPS carrier-phase measurements, by an integer number of cycles, caused by temporary signal loss [1]. Signal loss is caused by obstruction of the GPS satellite signal due to buildings, bridges, trees, and other objects (Figure 2.5). This is mainly because the GPS signal is a weak and noisy signal. Radio interference, severe ionospheric disturbance, and high receiver dynamics can also cause signal loss. Cycle slips could occur due to a receiver malfunction [1].
Cycle slips may occur briefly or may remain for several minutes or even more. Cycle slips could affect one or more satellite signals. The size of a cycle slip could be as small as one cycle or as large as millions of cycles. Cycle slips must be identified and corrected to avoid large errors in the computed coordinates. This can be done using several methods. Examining the so-called triple difference observable, which is formed by combining the GPS observables in a certain way (see Section 2.8), is the most popular in practice. A cycle slip will only affect one triple difference and therefore will appear as a spike in the triple difference data series. In some extreme cases, such as severe ionospheric activities, it might be difficult to correctly detect and repair cycle slips using triple difference observable [1, 3]. Visual inspection of the adjustment residuals might be useful to locate any remaining cycle slip.
Figure 2.5 GPS cycle slips.
Linear combinations of GPS observables
GPS measurements are corrupted by a number of errors and biases,which are difficult to model fully. The unmodeled errors and biases limit the positioning accuracy of the standalone GPS receiver. Fortunately, GPS receivers in close proximity will share to a high degree of similarity the same errors and biases. As such, for those receivers, a major part of the GPS error budget can simply be removed by combining their GPS observables.
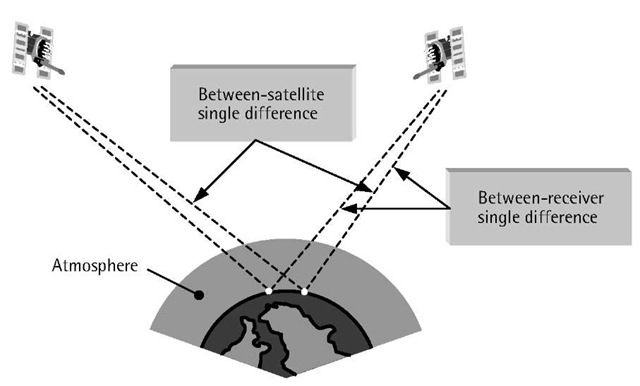
In principle, there are three groups of GPS errors and biases: satellite-related, receiver-related, and atmospheric errors and biases [3]. The measurements of two GPS receivers simultaneously tracking a particular satellite contain more or less the same satellite-related errors and atmospheric errors. The shorter the separation between the two receivers, the more similar the errors and biases. Therefore, if we take the difference between the measurements collected at these two GPS receivers, the satellite-related errors and the atmospheric errors will be reduced significantly.This linear combination is known as between-receiver single difference (Figure 2.6).
Similarly, the two measurements of a single receiver tracking two satellites contain the same receiver clock errors. Therefore, taking the difference between these two measurements removes the receiver clock errors. This difference is known as between-satellite single difference (Figure 2.6).
When two receivers track two satellites simultaneously, two between-receiver single difference observables could be formed. Subtracting these two single difference observables from each other generates the so-called double difference [3]. This linear combination removes the satellite and receiver clock errors. The other errors are greatly reduced. In addition, this observable preserves the integer nature of the ambiguity parameters. It is therefore used for precise carrier-phase-based GPS positioning.
Another important linear combination in known as the "triple difference," which results from differencing two double-difference observables over two epochs of time [3]. As explained in the previous section, the ambiguity parameters remain constant over time, as long as there are no cycle slips. As such, when forming the triple difference, the constant ambiguity parameters disappear. If, however, there is a cycle slip in the data, it will affect one triple-difference observable only, and therefore will appear as a spike in the triple-difference data series. It is for this reason that the triple-difference linear combination is used for detecting the cycle slips.
Figure 2.6 Some GPS linear combinations.
All of these linear combinations can be formed with a single frequency data, whether it is the carrier phase or the pseudorange observables. If dual-frequency data is available, other useful linear combinations could be formed. One such linear combination is known as the ionosphere-free linear combination.Based on this characteristic, the ionosphere-free observable combines the L1 and L2 measurements to essentially eliminate the ionospheric effect. The L1 and L2 carrier-phase measurements could also be combined to form the so-called wide-lane observable, an artificial signal with an effective wavelength of about 86 cm. This long wavelength helps in resolving the integer ambiguity parameters [1].