The ability of GPS to determine the precise location of a user anywhere, under any weather conditions, attracted millions of users worldwide from various fields and backgrounds. With advances in GPS and computer technologies, GPS manufacturers were able to come up with very user-friendly systems. However, one common problem that many newcomers to the GPS face is the issue of datums and coordinate systems, which require some geodetic background. This topic tackles the problem of datums and coordinate systems in detail. As in the previous topics, complex mathematical formulas are avoided. As many users are interested in the horizontal component of the GPS position, the issue of map projections is also introduced. For the sake ofcompleteness, the height systems are introduced as well, at the end of this topic.
What is a datum?
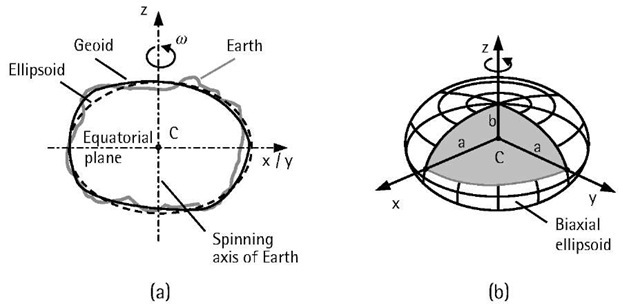
The fact that the topographic surface of the Earth is highly irregular makes it difficult for the geodetic calculations—for example, the determination of the user’s location—to be performed. To overcome this problem, geode-sists adopted a smooth mathematical surface, called the reference surface, to approximate the irregular shape of the earth (more precisely to approximate the global mean sea level, the geoid) [1, 2]. One such mathematical surface is the sphere, which has been widely used for low-accuracy positioning. For high-accuracy positioning such as GPS positioning, however, the best mathematical surface to approximate the Earth and at the same time keep the calculations as simple as possible was found to be the biaxial ellipsoid (see Figure 4.1). The biaxial reference ellipsoid, or simply the reference ellipsoid, is obtained by rotating an ellipse around its minor axis, b [2]. Similar to the ellipse, the biaxial reference ellipsoid can be defined by the semiminor and semimajor axes (a, b) or the semimajor axis and the flattening (a, f), where f = 1 – (b / a).
An appropriately positioned reference ellipsoid is known as the geodetic datum [2]. In other words, a geodetic datum is a mathematical surface, or a reference ellipsoid, with a well-defined origin (center) and orientation. For example, a geocentric geodetic datum is a geodetic datum with its origin coinciding with the center of the Earth. It is clear that there are an infinite number of geocentric geodetic datums with different orientations. Therefore, a geodetic datum is uniquely determined by specifying eight parameters: two parameters to define the dimension of the reference ellipsoid; three parameters to define the position of the origin; and three parameters to define the orientation of the three axes with respect to the earth. Table 4.1 shows some examples of three common reference systems and their associated ellipsoids [3].
In addition to the geodetic datum, the so-called vertical datum is used in practice as a reference surface to which the heights (elevations) of points are referred [2]. Because the height of a point directly located on the vertical datum is zero, such a vertical reference surface is commonly known as the surface of zero height. The vertical datum is often selected to be the geoid; the surface that best approximates the mean sea level on a global basis [see Figure 4.1(a)].
In the past, positions with respect to horizontal and vertical datums have been determined independent of each other [2]. However, with the advent of space geodetic positioning systems such as GPS, it is possible to determine the 3-D positions with respect to a 3-D reference system.
Figure 4.1 (a) Relationship between the physical surface of the Earth, the geoid, and the ellipsoid; and (b) ellipsoidal parameters.
Geodetic coordinate system
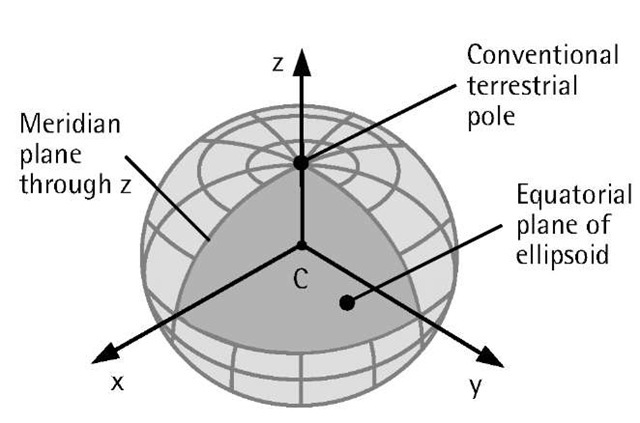
A coordinate system is defined as a set of rules for specifying the locations (also called coordinates) of points [4]. This usually involves specifying an origin of the coordinates as well as a set of reference lines (called axes) with known orientation. Figure 4.2 shows the case of a 3-D coordinate system that uses three reference axes (x, y, and z) that intersect at the origin (C) of the coordinate system.
Table 4.1 Examples of Reference Systems and Associated Ellipsoids
|
Reference Systems |
Ellipsoid |
fl(m) |
1/f |
|
WGS 84 |
WGS 84 |
6378137.0 |
298.257223563 |
|
NAD 83 |
GRS 80 |
6378137.0 |
298.257222101 |
|
NAD 27 |
Clarke 1866 |
6378206.4 |
294.9786982 |
Figure 4.2 3-D coordinate system.
Coordinate systems may be classified as one-dimensional (1-D), 2-D, or 3-D coordinate systems, according to the number of coordinates required to identify the location of a point. For example, a 1-D coordinate system is needed to identify the height of a point above the sea surface.
Coordinate systems may also be classified according to the reference surface, the orientation of the axes, and the origin. In the case of a 3-D geodetic (also known as geographic) coordinate system, the reference surface is selected to be the ellipsoid. The orientation of the axes and the origin are specified by two planes: the meridian plane through the polar or z-axis (a meridian is a plane that passes through the north and south poles) and the equatorial plane of the ellipsoid (see Figure 4.2 for details).
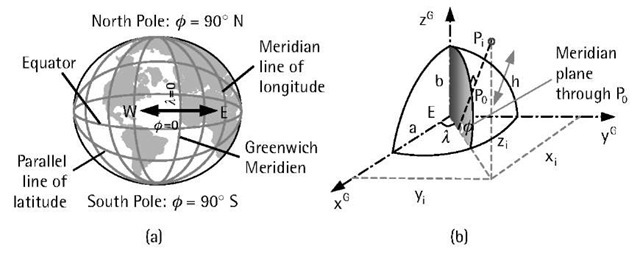
Of particular importance to GPS users is the 3-D geodetic coordinate system. In this system, the coordinates of a point are identified by the geodetic latitude
the geodetic longitude
and the height above the reference surface (h). Figure 4.3 shows these parameters. Geodetic coordinates
can be easily transformed to Cartesian coordinates (x, y, and z) as shown in Figure 4.3(b) [2]. To do this, the ellipsoidal parameters (a and f) must be known. It is also possible to transform the geodetic coordinates
into a rectangular grid coordinate (e.g., Northing and Easting) for mapping purposes [5].
Conventional Terrestrial Reference System
The Conventional Terrestrial Reference System (CTRS) is a 3-D geocentric coordinate system, that is, its origin coincides with the center of the Earth (Figure 4.2). The CTRS is rigidly tied to the Earth, that is, it rotates with the Earth [5]. It is therefore also known as the Earth-centered, Earth-fixed (ECEF) coordinate system.
Figure 4.3 (a) Concept of geodetic coordinates; and (b) geodetic and Cartesian coordinates.
The orientation of the axes of the CTRS is defined as follows: The z-axis points toward the conventional terrestrial pole (CTP), which is defined as the average location of the pole during the period 1900-1905 [3]. The x-axis is defined by the intersection of the terrestrial equatorial plane and the meridional plane that contains the mean location of the Greenwich observatory (known as the mean Greenwich meridian). It is clear from the definition of the x and z axes that the xz-plane contains the mean Greenwich meridian. The y-axis is selected to make the coordinate system right-handed (i.e., 90° east of the x-axis, measured in the equatorial plane). The three axes intersect at the center of the Earth, as shown in Figure 4.2.
The CTRS must be positioned with respect to the Earth (known as realization) to be of practical use in positioning [2]. This is done by assigning coordinate values to a selected number of well-distributed reference stations. One of the most important CTRSs is the International Terrestrial Reference System (ITRS), which is realized as the International Terrestrial Reference Frame (ITRF). The ITRF solution is based on the measurements from globally distributed reference stations using GPS and other space geodetic systems. It is therefore considered to be the most accurate coordinate system [6]. The ITRF is updated every 1 to 3 years to achieve the highest possible accuracy. The most recent version at the time of this writing is the ITRF2000.
The WGS 84 and NAD 83 systems
The World Geodetic System of 1984 (WGS 84) is a 3-D, Earth-centered reference system developed by the former U.S. Defense Mapping Agency now incorporated into a new agency, National Imagery and Mapping Agency (NIMA). It is the official GPS reference system. In other words, a GPS user who employs the broadcast ephemeris in the solution process will obtain his or her coordinates in the WGS 84 system. The WGS 84 utilizes the CTRS combined with a reference ellipsoid that is identical, up to a very slight difference in flattening, with the ellipsoid of the Geodetic Reference System of 1980 (GRS 80); see Table 4.1. The latter was recommended by the International Association of Geodesy for use in geodetic applications [5]. WGS 84 was originally established (realized) using a number of Doppler stations. It was then updated several times to bring it as close as possible to the ITRF reference system. With the most recent update, WGS 84 is coincident with the ITRF at the subdecimeter accuracy level [7].
In North America, another nominally geocentric datum, the North American Datum of 1983 (NAD 83), is used as the legal datum for spatial positioning. NAD 83 utilizes the ellipsoid of the GRS 80, which means that the size and shape of both WGS 84 and NAD 83 are almost identical. The original realization of NAD 83 was done in 1986, by adjusting "primarily" classical geodetic observations that connected a network of horizontal control stations spanning North America, and several hundred observed Doppler positions. Initially, NAD 83 was designed as an Earth-centered reference system [8]. However, with the development of more accurate techniques, it was found that the origin of NAD 83 is shifted by about 2m from the true Earth’s center. In addition, access to NAD 83 was provided mainly through a horizontal control network, which has a limited accuracy due to the accumulation of errors. To overcome these limitations, NAD 83 was tied to ITRF using 12 common, very long baseline interferometry (VLBI) stations located in both Canada and the United States (VLBI is a highly accurate, yet complex, space positioning system). This resulted in an improved realization of the NAD 83, which is referred to as NAD 83 (CSRS) and NAD 83 (NSRS) in both Canada and the United States, respectively [8]. The acronyms CSRS and NSRS refer to the Canadian Spatial Reference System and National Spatial Reference System, respectively. It should be pointed out that, due to the different versions of the ITRF, it is important to define to which epoch the ITRF coordinates refer.
What coordinates are obtained with GPS?
The satellite coordinates as given in the broadcast ephemeris will refer to the WGS 84 reference system. Therefore, a GPS user who employs the broadcast ephemeris in the adjustment process will obtain his or her coordinates in the WGS 84 system as well. However, if a user employs the precise ephemeris obtained from the IGS service,his or her solution will be referred to the ITRF reference system. Some agencies provide the precise ephemeris in various formats. For example, Geomatics Canada provides its precise ephemeris data in both the ITRF and the NAD 83 (CSRS) formats.
The question that may arise is what happens if the available reference (base) station coordinates are in NAD 83 rather than in WGS 84? The answer to this question varies, depending on whether the old or the improved NAD 83 system is used. Although the sizes and shapes of the reference ellipsoids of the WGS 84 and the old NAD 83 are almost identical; their origins are shifted by more than 2m with respect to each other [3]. This shift causes a discrepancy in the absolute coordinates of points when expressed in both reference systems. In other words, a point on the Earth’s surface will have WGS 84 coordinates that are different from its coordinates in the old NAD 83. The largest coordinate difference is in the height component (about 0.5m). However, the effect of this shift on the relative GPS positioning is negligible. For example, if a user applies the NAD 83 coordinates for the reference station instead of its WGS 84, his or her solution will be in the NAD 83 reference system with a negligible error (typically at the millimeter level). The improved WGS 84 and the NAD 83 systems are compatible.
Datum transformations
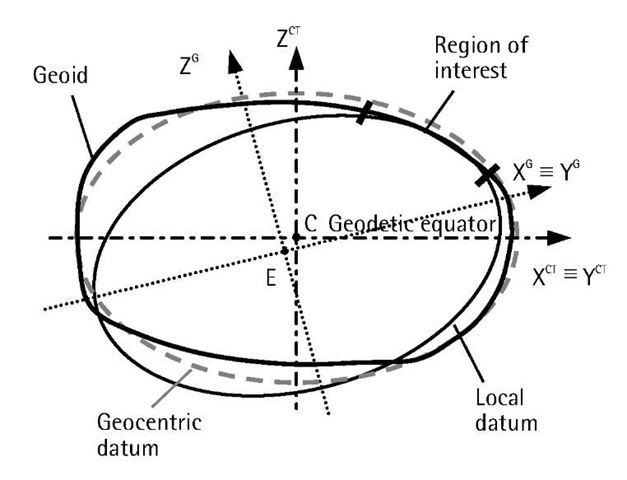
As stated in Section 4.1, in the past, positions with respect to horizontal and vertical datums have been determined independent of each other [2]. In addition, horizontal datums were nongeocentric and were selected to best fit certain regions of the world (Figure 4.4). As such, those datums were commonly called local datums. More than 150 local datums have been used by different countries of the world. An example of the local datums is the North American datum of 1927 (NAD 27). With the advent of space geodetic positioning systems such as GPS, it is now possible to determine global 3-D geocentric datums.
Figure 4.4 Geocentric and local datums.
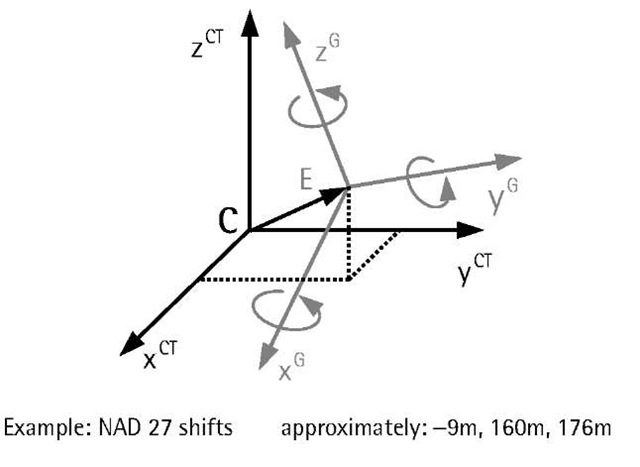
Old maps were produced with the local datums, while new maps are mostly produced with the geocentric datums. Therefore, to ensure consistency, it is necessary to establish the relationships between the local datums and the geocentric datums, such as WGS 84. Such a relationship is known as the datum transformation (see Figure 4.5). NIMA has published the transformation parameters between WGS 84 and the various local datums used in many countries. Many GPS manufacturers currently use these parameters within their processing software packages. It should be clear, however, that these transformation parameters are only approximate and should not be used for precise GPS applications. In Toronto, for example, a difference as large as several meters in the horizontal coordinates is obtained when applying NIMA’s parameters (WGS 84 to NAD 27) as compared with the more precise National Transformation software (NTv2) produced by Geomatics Canada. Such a difference could be even larger in other regions. The best way to obtain the transformation parameters is by comparing the coordinates of well-distributed common points in both datums.
Figure 4.5 Datum transformations.
