Introduction
Traditionally, the perception of three-dimensional (3D) scenes and objects was assumed to be the result of the reconstruction of 3D surfaces from available depth cues, such as binocular disparity, motion parallax, texture, and shading (Marr, 1982). In this approach, the role of figure-ground organization was kept to a minimum. Figure-ground organization refers to finding objects in the image, differentiating them from the background, and grouping contour elements into two-dimensional (2D) shapes representing the shapes of the 3D objects. According to Marr, solving figure-ground organization was not necessary. The depth cues could provide the observer with local estimates of surface orientation at many points. These local estimates were then integrated into the estimates of the visible parts of 3D shapes. Marr called this a 2.5D representation. If the objects in the scene are familiar, their entire 3D shapes can be identified (recognized) by matching the shapes in the observer’s memory to the 2.5D sketch. If they are not familiar, the observer will have to view the object from more than one viewing direction and integrate the visible surfaces into the 3D shape representations.
Reconstruction and recognition of surfaces from depth cues might be possible, although there has been no computational model that could do it reliably. Human observers cannot do it reliably, either. These failures suggest that the brain may use another method to recover 3D shapes, a method that does not rely on depth cues as the only or even the main source of shape information. Note that there are two other sources of information available to the observer: the 2D retinal shapes produced by figure-ground organization and 3D shape priors representing the natural world statistics. Figure-ground organization was defined in the first paragraph and will be discussed next. The 3D shape priors include 3D symmetry and 3D compactness. These priors have been recently used by the present authors in their models of 3D shape perception (Pizlo, 2008; Sawada and Pizlo, 2008a; Li, 2009; Li, Pizlo, and Steinman, 2009; Sawada, 2010; Pizlo et al., 2010), and they will be discussed in the following section.
Figure-Ground Organization
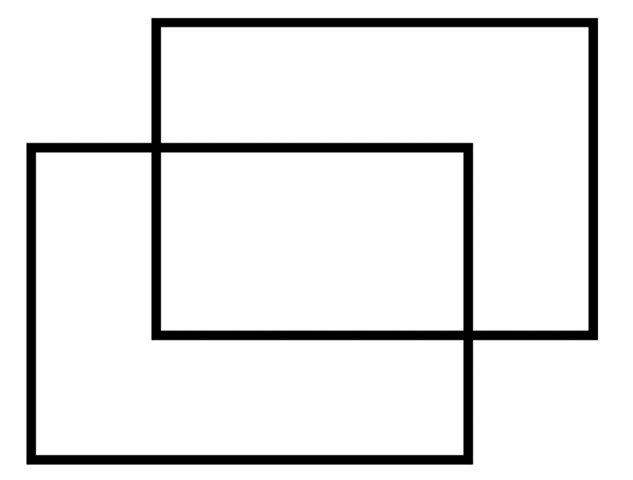
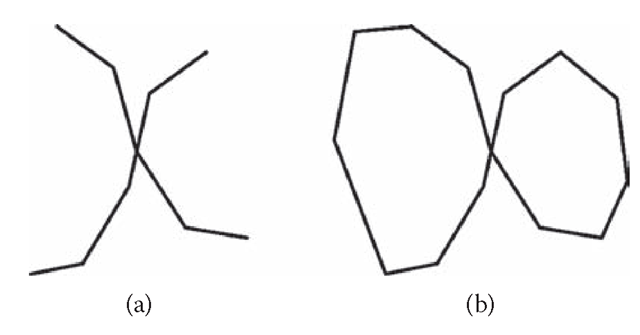
The concept of figure-ground organization was introduced by Gestalt psychologists in the first half of the 20th century (Wertheimer, 1923/1958; Koffka, 1935). Gestalt psychologists emphasized the fact that we do not perceive the retinal image. We see objects and scenes, and we can perceptually judge their shapes, sizes, and colors, but we cannot easily (if at all) judge their retinal images. The fact that we see shapes, sizes, and colors of objects veridically despite changes in the viewing conditions (viewing orientation, distance, and chromaticity of the illuminant) is called shape, size, and color constancy, respectively. Changes in the viewing conditions change the retinal image, but the percept remains constant. How are those constancies achieved? Gestalt psychologists pointed out that the percept can be explained by the operation of a simplicity principle. Specifically, according to Gestaltists, the percept is the simplest interpretation of the retinal image. Figures 6.1 and 6.2 provide illustrations of how a simplicity principle can explain the percept. Figure 6.1 can be interpreted as two overlapping rectangles or two touching hexagons. It is much easier to see the former interpretation because it is simpler. Clearly, two symmetric rectangles is a simpler interpretation than two asymmetric hexagons. Figure 6.2a can be interpreted as two lines forming an X or two V-shaped lines touching at their vertices (the Vs are perceived as either vertical or horizontal).
FIGURE 6.1 Two rectangles is a simpler interpretation than two concave hexagons.
The reader is more likely to see the former interpretation because it is simpler. In Figure 6.2b, the reader perceives two closed shapes touching each other. Note that Figure 6.2b was produced from Figure 6.2a by “closing” two horizontal Vs. Closed 2D shapes on the retina are almost always produced by occluding contours of 3D shapes. Therefore, this interpretation is more likely. So, global closure is likely to change the local interpretation of an X. The fact that spatially global aspects, such as closure, affect spatially local percepts refutes Marr’s criticism of Gestalt psychology. Marr (1982) claimed that all examples of perceptual grouping can be explained by recursive application of local operators of proximity, similarity, and smoothness. If Marr were right, than the perceptual “whole would be equal to the sum of its parts.” Figure 6.2b provides a counterexample to Marr’s claim. In general, forming perceptual shape cannot be explained by summing up the results of spatially local operators. The operators must be spatially global.
FIGURE 6.2 Spatially global features (closure) affect spatially local decisions. (a) This figure is usually perceived as two smooth lines forming an X intersection. (b) This figure is usually perceived as two convex polygons touching each other at one point. Apparently, closing the curves changes the interpretation at the intersection, even though the image around the intersection has not changed.
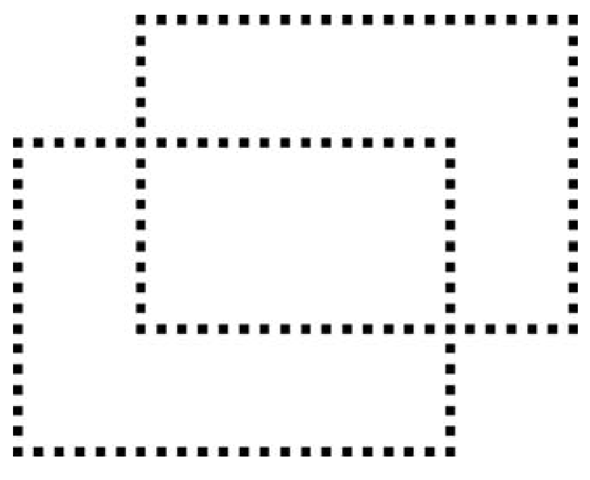
It is clear that the percept is more organized, richer, simpler, as well as more veridical than the retinal image. This fact demonstrates that the visual system adds information to the retinal image. Can this “configural-ity” effect be formalized? Look again at Figure 6.1. You see two “perfect” rectangles. They are perfect in the sense that the lines representing edges are perceived as straight and smooth. This is quite remarkable considering the fact that the output of the retina is more like that shown in Figure 6.3. Specifically, the retinal receptors provide a discrete sampling of the continuous retinal image, and the sampling is, in fact, irregular. The percept of continuous edges of the rectangles can be produced by interpolation and smoothing. Specifically, one can formulate a cost function with two components: the first evaluates the difference (error) between the perceptual interpretation and the data, and the second evaluates the complexity of the perceptual interpretation. The percept corresponds to the minimum of the cost function. Clearly, two rectangles with straight-line edges are a better (simpler) interpretation than a set of unrelated points, or than two rectangles with jagged sides. This example shows that the traditional, Fechnerian approach to perception is inadequate.
According to Fechner’s (1860/1966) approach, the percept is a result of retinal measurements. It seems reasonable to think that such properties of the retinal image as light intensity or position could be measured by the visual system.
FIGURE 6.3 When the retinal image is like that in Figure 6.1, the input to the visual system is like that shown here. Despite the fact that the input is a set of discrete points, we see continuous rectangles when we look at Figure 6.1.
It is less obvious how 3D shape can be measured on the retina. When we view a Necker cube monocularly, we see a cube. This percept cannot be a direct result of retinal measurement, because this 2D retinal image is actually consistent with infinitely many 3D interpretations. The only way to explain the percept is to assume that the visual system “selects” the simplest 3D interpretation. Surely, a cube, an object with multiple symmetries, is the simplest 3D interpretation of any of the 2D images of the cube (except for several degenerate views). Note also that a cube is a maximally compact hexahedron. That is, a cube is a polyhedron with six faces whose volume is maximal for a given surface area. Recall that both symmetry and compactness figured prominently in the writings of the Gestalt psychologists (Koffka, 1935).
We now know that it is more adequate to “view” 3D shape perception as an inverse problem, rather than as a result of retinal measurements (Pizlo, 2001, 2008). The forward (direct) problem is represented by the retinal image formation. The inverse problem refers to the perceptual inference of the 3D shape from the 2D image. This inverse problem is ill posed and ill conditioned, and the standard (perhaps even the only) way to solve it is to impose a priori constraints on the family of possible 3D interpretations (Poggio, Torre, and Koch, 1985). In effect, the constraints make up for the information lost during the 3D to 2D projection. The resulting perceptual interpretation is likely to be veridical if the constraints represent regularities inherent in our natural world (natural world statistics). If the constraints are deterministic, one should use regularization methods. If the constraints are probabilistic, one should use Bayesian methods. Deterministic methods are closer to the concept of a Gestalt simplicity principle, whereas probabilistic methods are closer to the concept of a likelihood principle, often favored by empiricists. Interestingly enough, these two methods are mathematically equivalent, as long as simplicity is formulated as an economy of description. This becomes quite clear in the context of a minimum description length approach (Leclerc, 1989; Mumford, 1996). The close relation between simplicity and likelihood was anticipated by Mach (1906/1959) and discussed more recently by Pomerantz and Kubovy (1986). Treating visual perception as an inverse problem is currently quite universal, especially among computational modelers. This approach has been used to model binocular vision, contour, motion, color, surface, and shape perception (for a review, see Pizlo, 2001).
It follows that if one is interested in studying the role of a priori constraints in visual perception, one should use distal stimuli that are as different from their retinal images as possible. This naturally implies that the distal stimuli should be 3D objects or images of 3D objects. In such cases, the visual system will have to solve a difficult inverse problem, and the role of constraints can be easily observed. If 2D images are distal stimuli, as in the case of examples in Figures 6.1, 6.2, and 6.3, a priori constraints may or may not be involved depending on whether the visual system “tries” to solve an inverse problem. As a result, the experimenter may never know which, if any, constraints are needed to explain a given percept. Furthermore, veridicality and constancy of the percept are poorly, if at all, defined with such stimuli. Also, if effective constraints are not applied to a given stimulus, then the inverse problem remains ill posed and ill conditioned. This means that the subjects’ responses are likely to vary substantially from condition to condition. In such a case, no single model will be able to explain the results. This may be the reason for why the demonstrations involving 2D abstract line drawings are so difficult to explain by any single theory. Figure-ground organization and amodal completion are hard to predict when the distal stimulus is 2D. We strongly believe that figure-ground organization should be studied with 3D objects. Ambiguities rarely arise with images of natural 3D scenes, because the visual system can apply effective constraints representing natural world statistics.
We want to point out that perceptual mechanisms underlying figure-ground organization are still largely unknown. But we hope that our 3D shape recovery model will make it easier to specify the requirements for the output of figure-ground organization. Once the required output of this process is known, it should be easy to study it. The next section describes our new model of 3D shape recovery. A discussion of its implications is presented in the last section.
Using Simplicity Principle to Recover 3D Shapes
We begin by observing that 3D shape is special because it is a complex perceptual characteristic, and it contains a number of regularities. Consider first the role of complexity. Shapes of different objects tend to be quite different. They are different enough so that differently shaped objects never produce identically shaped retinal images. For example, a chair and a car will never produce identically shaped 2D retinal images, regardless of their viewing directions, and similarly with a teapot, apple, and so forth. This implies that each 3D shape can be uniquely recognized from any of its 2D images. This fact is critical for achieving shape constancy. More precisely, if the observer is familiar with the 3D shape, whose image is on his or her retina, this shape can be unambiguously identified. What about the cases when the 3D shape is unfamiliar? Can an unfamiliar shape be perceived veridically? The answer is yes, as long as the observer’s visual system can apply effective shape constraints to perform 3D shape recovery. Three-dimensional symmetry is one of the most effective constraints. It reduces the ambiguity of the shape recovery problem substantially. The role of 3D symmetry will be explained next.
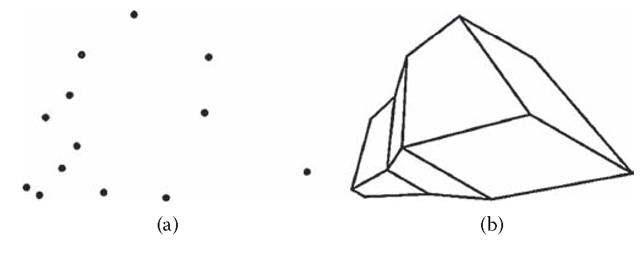
Figure 6.4a consists of 13 points, images of vertices of a 3D symmetric polyhedron shown in Figure 6.4b. The polyhedron in Figure 6.4b is perceived as a 3D shape; the points in Figure 6.4a are not. The points in Figure 6.4a are perceived as lying on the plane of the page. Formally, when a single 2D image of N unrelated points is given, the 3D reconstruction problem involves N unknown parameters, the depth values of all points. The problem is so underconstrained that the visual system does not even “attempt” to recover a 3D structure. As a result, we see 2D, not 3D, points. When points form a symmetric configuration in the 3D space, the reconstruction problem involves only one (rather than N) unknown parameter—namely, the 3D aspect ratio of the configuration (Vetter and Poggio, 1994; Li, Pizlo, and Steinman, 2009; Sawada, 2010). Note that the visual system must organize the retinal image first and (1) determine that the image could have been produced by a 3D symmetric shape and (2) identify which pairs of image features are actually symmetric in the 3D interpretation.
Figure 6.4 Static depth effect. The three-dimensional (3D) percept produced by looking at (b) results from the operation of 3D symmetry constraint when it is applied to an organized retinal image. The percept is not 3D when the retinal image consists of a set of unrelated points, like that in (a).
These two steps can be accomplished when the 2D retinal image is organized into one or more 2D shapes. Clearly, the visual system does this in the case of Figure 6.4b, but not Figure 6.4a. The only difference between the two images is that the individual points are connected by edges in Figure 6.4b. Obviously, the edges are not drawn arbitrarily. The edges in the 2D image correspond to edges of a polyhedron in the 3D interpretation. The difference between Figure 6.4a and Figure 6.4b is striking: the 3D percept in the case of Figure 6.4b is automatic and reliable. In fact, the reader cannot avoid seeing a 3D object no matter how hard he or she tries. Just the opposite is true with Figure 6.4a. It is impossible to see the points as forming a 3D configuration. Adding “meaningful” edges to 2D points is at least as powerful as adding motion in the case of kinetic depth effect (Wallach and O’Connell, 1953). We might, therefore, call the effect presented in Figure 6.4, a static depth effect (SDE).
How does symmetry reduce the uncertainty in 3D shape recovery? In other words, what is the nature of a symmetry constraint? A 3D reflection cannot be undone, in a general case, by a 3D rigid rotation, because the determinant of a reflection matrix is “-1,” whereas the determinant of a rotation matrix is “+1.” However, a 3D reflection is equivalent to (can be undone by) a 3D rotation when a 3D object is mirror symmetric. It follows that, given a 2D image of a 3D symmetric object, one can produce a virtual 2D image of the same object, by computing a mirror image of the 2D real image. This is what Vetter and Poggio (1994) did. A 2D virtual image is a valid image of the same 3D object, only if the object is mirror symmetric. So, a 3D shape recovery from a single 2D image turns out to be equivalent to a 3D shape recovery from two 2D images, when the 3D shape is mirror symmetric. It had been known that two 2D orthographic images determine the 3D interpretation with only one free parameter (Huang and Lee, 1989).
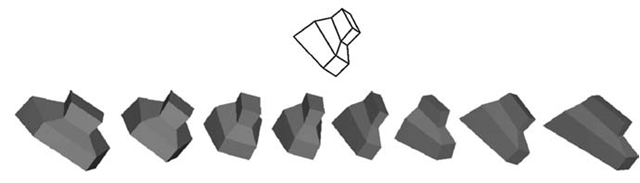
The fact that a mere configuration of points and edges in the 2D image gives rise to a 3D shape perception encouraged us to talk about 3D shape recovery, as opposed to reconstruction. The 3D shape is not actually constructed from individual points. Instead, it is produced (recovered) in one computational step. The one-parameter family of 3D symmetric interpretations consistent with a single 2D orthographic image is illustrated in Figure 6.5. The 2D image (line drawing) is shown on top. The eight shaded objects are all mirror symmetric in 3D, and they differ from one another with respect to their aspect ratio. The objects on the left-hand side are wide, and the objects on the right-hand side are tall. There are infinitely many such 3D symmetric shapes.
FIGURE 6.5 The shaded three-dimensional (3D) objects illustrate the one-parameter family of 3D shapes that are possible 3D symmetric interpretations of the line drawing shown on top.
Their aspect ratio ranges from infinitely large to zero. Each of these objects can produce the 2D image shown on top. How does the visual system decide among all these possible interpretations? Which one of these infinitely many 3D shapes is most likely to become the observer’s percept? We showed that the visual system decides about the aspect ratio of the 3D shape by using several additional constraints: maximal 3D compactness, minimum surface area, and maximal planarity of contours (Sawada and Pizlo, 2008a; Li, Pizlo, and Steinman, 2009; Pizlo et al., 2010). These three constraints actually serve the purpose of providing an interpretation (3D recovered shape) that does not violate the nonaccidental (generic) viewpoint assumption. Specifically, the recovered 3D shape is such that the projected image would not change substantially under small or moderate changes in the viewing direction of the recovered 3D shape. In other words, the 3D recovered shape is most likely. This means that it is also the simplest (Pizlo, 2008).
Several demonstrations illustrating the quality of 3D shape recovery from a single 2D image can be viewed at http://www1.psych.purdue .edu/~sawada/minireview/. In Demo 1, the shapes are abstract, randomly generated polyhedra. In Demo 2, images of 3D models of real objects, as well as real images of natural objects are used. In Demo 3, images of human bodies are used. In all these demos, the 2D contours (and skeletons) were drawn by hand and “given” to the model. First, consider the images of randomly generated polyhedra, like those in Figure 6.4b (go to Demo 1). The 2D image contained only the relevant contours—that is, the visible contours of the polyhedron. The model had information about where the contours are in the 2D image and which points and which contours are symmetric in 3D. Obviously, features that are symmetric in 3D space are not symmetric in the 2D image. Instead, they are skew-symmetric (Sawada and Pizlo, 2008a, 2008b). There is an invariant of the 3D to 2D projection of a mirror-symmetric object. Specifically, the lines connecting the 2D points that are images of pairs of 3D symmetric points are all parallel to one another in any 2D orthographic image, and they intersect at a single point (called a vanishing point) in any 2D perspective image. This invariant can be used to determine automatically the pairs of 2D points that are images of 3D symmetric points. Finally, the model had information about which contours are planar in 3D. Planarity constraint is critical in recovering the back, invisible part of the 3D shape (Li, Pizlo, and Steinman, 2009). We want to point out, again, that the information about where in the image the contours are and which contours are symmetric and which are planar in 3D corresponds to establishing figure-ground organization in the 2D image. Our model does not solve the figure-ground organization (yet). The model assumes that figure-ground organization has already been established. It is clear that the model recovered these polyhedral shapes very well. The recovered 3D shapes are accurate for most shapes and most viewing directions. That is, the model achieves shape constancy. Note that the model can recover the entire 3D shape, not only its front, visible surfaces. The 3D shapes recovered by the model were similar to the 3D shapes recovered by human observers (Li, Pizlo, and Steinman, 2009).
Next, consider examples with 3D real objects (Demo 2). One of us marked the contours in the image by hand. Note that the marked contours were not necessarily straight-line segments. The contours were curved, and they contained “noise” due to imperfect drawing. The reader realizes that marking contours of objects in the image is easy for a human observer; it seems effortless and natural. However, we still do not know how the visual system does it. After the contours were drawn, the pairs of contours that are symmetric in 3D and the contours that are planar were labeled by hand. Because objects like a bird or a spider do not have much volume and the volume is not clearly specified by the contours, the maximum compactness and minimum surface area constraints were applied to the convex hull of the 3D contours. The convex hull of a set of points is the smallest 3D region containing all the points in its interior or on its boundary. Again, it can be seen that the 3D shapes were recovered by the model accurately. Furthermore, the recovered 3D shapes are essentially identical to the shapes perceived by the observer. Our 3D shape recovery model seems to capture all the essential characteristics of human visual perception of 3D shapes.
Finally, consider the case of images of models of human bodies. Note that two of the three human models are asymmetric. The skeletons of humans were marked by hand, and the symmetric parts of skeletons were manually identified, as in the previous demos. Marking skeletons was no more difficult than marking contours in synthetic images. The most interesting aspect of this demo is the recovery of asymmetric human bodies. The human body is symmetric in principle, but due to changes in the position and orientation of limbs, the body is not symmetric in 3D. Interestingly, our model is able to recover such 3D asymmetric shapes. The model does it by first correcting the 2D image (in the least squares sense) so that the image is an image of a symmetric object. Then, the model recovers the 3D symmetric shape and uncorrects the 3D shape (again, in the least squares sense), so that the 3D shape is consistent with the original 2D image (Sawada and Pizlo, 2008a; Sawada, 2010). The recovered 3D shape is not very different from the true 3D shape and from the perceived 3D shape.
Summary and Discussion
We described the role of 3D mirror symmetry in the perception of 3D shapes. Specifically, we considered the classical problem of recovering 3D shapes from a single 2D image. Our computational model can recover the 3D structure (shape) of curves and contours whose 2D image is identified and described. Finding contours in a 2D image is conventionally referred to as figure-ground organization. The 3D shape is recovered quite well, and the model’s recovery is correlated with the recovery produced by human observers. Once the 3D contours are recovered, the 3D surfaces can be recovered by interpolating the 3D contours (like wrapping the 3D surfaces around the 3D contours) (Pizlo, 2008; Barrow and Tenenbaum, 1981). It follows that our model is quite different from the conventional, Marr-like approach. In the conventional approach, 3D visible surfaces (2.5D sketch) were reconstructed first. Next, the “2.5D shape” was produced by changing the reference frame from viewer centered to object centered. But does a 2.5D representation actually have shape? Three-dimensional shape refers to spatially global geometrical characteristics of an object that are invariant under rigid motion and size scaling. However, 3D surfaces are usually described by spatially local features such as bumps, ridges, and troughs. Surely, specifying the 3D geometry of such surface features does say something about shape, but spatially local features are not shapes. Spatially local features have to be related (connected) to one another to form a “whole.” Three-dimensional symmetry is arguably the best, perhaps even the only way to provide such a relational structure and, thus, to represent shapes of 3D objects. But note that visible surfaces of a 3D symmetric shape are never symmetric (except for degenerate views). If symmetry is necessary for shape, then arbitrary surfaces may not have shape. At least, they may not have shape that can lead to shape constancy with human observers and computational models.
Can our model be generalized to 3D shapes that are not symmetric? The model can already be applied to nearly symmetric shapes (see Demo 3). For a completely asymmetric shape, the model can be applied as long as there are other 3D constraints that can substantially reduce the family of possible 3D interpretations. Planarity of contours can do the job, as shown with an earlier version of our shape recovery model (Chan et al., 2006). Planarity of contours can often reduce the number of free parameters in 3D shape recovery to just three (Sugihara, 1986). With a three-parameter family of possible interpretations, 3D compactness and minimum surface area are likely to lead to a unique and accurate recovery. This explains why human observers can achieve shape constancy with asymmetric polyhedra, although shape constancy is not as reliable as with symmetric ones.
Finally, we will briefly discuss the psychological and physiological plausibility of one critical aspect of our model. Recall that the model begins with computing a virtual 2D image, which is a mirror reflection of a given 2D real image. Is there evidence suggesting that the human visual system computes 2D virtual images? The answer is “yes.” When the observer is presented with a single image of a 3D object, he or she will memorize not only this image, but also its mirror reflection (Vetter, Poggio, and Bülthoff, 1994). Note that a mirror image of a given 2D image of a 3D object is useless unless the 3D object is symmetric. When a 3D object is asymmetric, the virtual 2D image is not a valid image of this object. This means that the observer will never be presented with a virtual image of an object, unless the 3D object is mirror symmetric. When the object is mirror symmetric, then a 2D virtual image is critical, because it makes it possible to recover the 3D shape. The computation of a virtual image has been demonstrated not only in psychophysical but also in electrophysi-ological experiments (Logothetis, Pauls, and Poggio, 1995; Rollenhagen and Olson, 2000).